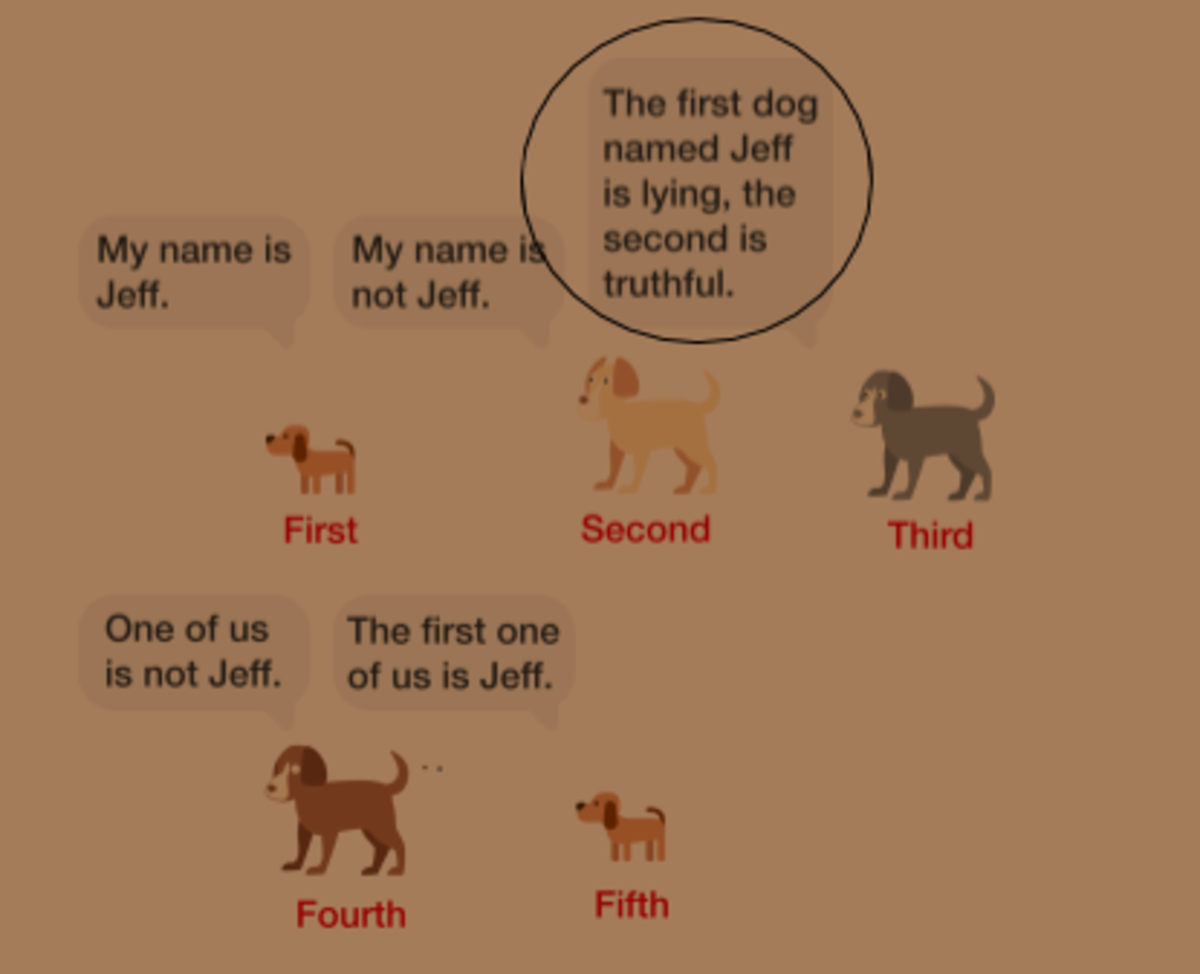
Jeffs

I used logic to answer this question. What I did first is read all the things that the dogs were saying. But, the one that caught my eye was the 3rd dog, this is because he said “the first dog named Jeff is lying, the second is truthful". But, if the 3rd dog is saying the truth, that means that the first and second dog are not named Jeff which is not possible because in the question it says that out of the 5 dogs, 4 are named Jeff and the third dog is basically saying that there are 3 named Jeff. So, the third dog is lying.

Suppose the first dog is not named Jeff. Then the first and fifth dogs are lying, but there is only one liar. This is a contradiction.

So the first dog is instead named Jeff and is telling the truth. This makes the third dog the liar, since it claims the first dog named Jeff is lying.

This incidentally means the second dog is telling the truth, and so is the dog not named Jeff.

The third dog because if we consider him true then the First one is false and second is true. But it cant be possible as we know that there 4 jeff .

I used logic to arrive to my answer. I know that 2 dogs can’t be named Jeff, so the third one is lying because of his statement. He says

If he tells the truth, then two dogs are not named Jeff, because his statement states that both dogs are not named Jeff. Therefore, he is lying.

The third dog is lying because if what he says is true then there will be 2 dogs that are not named Jeff, which is not possible. My Name Jeff! :D

The third dog claims that first dog is lying. But this makes both first dog and fifth dog the liar. But there is only one liar.

Hence the third dog must be the liar.

The first and fifth dog cannot be lying. If the first dog is lying, then the fifth must be telling the truth, which creates a contradiction. If the fifth dog is lying, then the first must be telling truth, which is not possible. The third claims the first is lying, which is not possible, therefore the third must be lying.

Assume that the first dog is lying, then the first dog is not a Jeff, Then the second dog who says his name is not Jeff is also lying and we have two liars which contradicts the given fact that exactly one dog is lying. Therefore, the first dog cannot be a liar and is a Jeff. Therefore, the third dog must be lying, because he says that the first dog is lying. And we can also conclude that the second dog is telling the truth and is not a Jeff, because there cannot be two liars. The fourth dog's statement "One of us is not Jeff." is a given truth. And the fifth dog's statement agrees that the first dog is a Jeff. The liar is thus the third dog .

I think the third dog is lying. Why? It just gave us way too much information. Lol! He's saying that neither the first nor the second dogs are named Jeff, but we are told that four dogs are named Jeff. Honestly, I think so because the first and the fifth dogs point to the same dog as Jeff, but the third one contradicts them. Actually, if the fifth dog is lying, then the first one has to be, too. So we can rule out the fifth dog as the liar. We know that at least one dog is Jeff (4 really are) and, therefore, we can rule out the fourth dog as the liar as well. If the fifth dog is not the liar, then the first dog must be Jeff. That means the first dog is also being truthful. It follows that the second dog is also telling the truth when he says that he is not Jeff. So yeah, the liar is the third dog.

What got my attention was the first and the fifth dog. The first says that he is Jeff, and the fifth says that the first is Jeff. If only one dog is lying, then the 1st and the 5th are both telling the truth. So, the lier it's the 3rd dog, because he said the 1st isn't Jeff.

First dog and last dog are saying the same thing, so they cannot be both liars and hence the first dog is named Jeff. Third dog calls first dog Jeff a liar and hence he’s telling a lie about the lying.

'The first dog named Jeff is lying' means that the third dog knows the first dog is Jeff.

The third dog says "the first dog named Jeff is lying, the second is truthful" he is confirming that the name of the first dog is Jeff so the first is not lying, and the third also says that the second is truthful (the second says his name is NOT Jeff) other reason why the first is not lying about his name making the third dog the liar.

The fourth dog is telling the truth since his statement is a given condition of the puzzle.

The fifth dog is telling the truth, since if he is lying then the first dog is not named Jeff and also lying, too many liars.

First dog is telling the truth and named Jeff since if the first dog is lying he is not named Jeff, then the second dog is also lying since there is only one dog not named Jeff and only one liar.

The second dog is telling the truth and not named Jeff. Otherwise, the true statement (with second as the only liar) of the third dog negates the true statement of the first dog, again too many liars.

That leaves only the third dog as liar. There is something odd about that since only part of his statement is actually false "The first dog named Jeff is lying" while the second part "the second is truthful" is true. We must regard his whole statement as an AND when either clause being false renders the entire statement false.

I think is, we can exclude the second and fourth dog, then there left 3 dogs, what the first one and the fifth one are telling, means the same, since there is only exactly one dog is lying, it should only be the third one.

First shot comes up when the 3rd dog says " The first dog named JEFF is lying" That itself is a contradictory statement. So better off I checked and verified my doubt on the dog and found that YES liar is the 3rd one.

the easiest of all the puzzles I've seen so far. If the 3rd dog was telling the truth then there would be 2 dogs not called jeff. But we know there is only one, so the 3rd dog must be lying.

The fifth dog says the first dog is telling the truth and the third dog says the first Jeff is lying so if he was Jeff he'd be lying but he is Jeff so the third dog is lying, because to the third dogs statement the fifth dog could not be lying

Premises: P1) There is 1 dog NOT named Jeff P2) There is 1 dog NOT telling the truth accurately

As is often the case in these sorts of problems, one of the dogs refers to the truth or falsehood of others, and becomes pivotal. Either this dog is telling the truth and identifies the liar, or this dog is the liar. We will come back to this shortly, after examining the claims in a more general sense...

1) Dog 1 is Jeff 2) Dog 2 is notJeff 3) The first Dog who is also Jeff is lying; the second Dog who is also Jeff is telling the truth. 4) There is 1 dog NOT named Jeff 5) Dog 1 is Jeff

From this, we can note: 1 = 5 P1 = 4

This means 1, 4, and 5 must all be true. As Dog 4 is simply restating Premise 1, it cannot be lying. Because Dogs 1 and 5 cannot both be lying (this would conflict with Premise 2), they must both be telling the truth.

Therefore, we know that Dog 1 is one of our Jeffs.

We can now examine Dog 3's claim in this context, and it immediately falls apart, because claim 3 contains two sub-claims. 3a) The first dog named Jeff is lying 3b) The second dog named Jeff is telling the truth

What 3a actually means is... 3a.i) If Dog 1 is Jeff, Dog 1 is lying 3a.ii) If Dog 1 is not Jeff, Dog 2 is Jeff 3a.iii) If Dog 1 is not Jeff, Dog 2 is lying. This is because, with only one non-Jeff dog allowed, one of the first two dogs must be named Jeff.

The problem should become immediately apparent: 1) Dog 1 is Jeff 3a) If Dog 1 is Jeff, Dog 1 is lying Therefore, Dog 1 is lying.

We then invert Dog 1's claim... which is that Dog 1 is Jeff. Therefore, Dog 1 is not Jeff. This would make Dog 5 be lying, which is impermissible (conflict with premises), as well as Dog 2 (3a.iii), causing a cascade to 3 separate lies.

As such, Dog 3 must be the liar. Dog 2 is not named Jeff and is telling the truth.

Third dog says, "the first dog named Jeff..." and then "..is lying". Its statement is contradicting itself!

The third dog caught my eye first, so I looked at what he was saying. He was saying the first dog was lying, but the first dog couldn’t be because he and the fifth dog were saying “one of us is Jeff” and “one of us is not Jeff.” So if the first dog is lying, the fifth one would be too but there is only one dog lying. Therefore, I can presume that the third dog is lying.

"all of the dogs are aware of who is named Jeff and who is the liar"...So only 1 is a liar. 1st and 5th agree that 1st one is Jeff. which only means the 3rd is a liar.

The anthropomorphic approach suggests the third dog is the liar. Most liars use a overly complicated scenario to present their untruth therefore the third dog is the liar, sorry not to use logic for this one.

If the third dog is truthful, then both Dog 1 and Dog 2 are not named Jeff.

This leaves 3 dogs being named Jeff. This is contradicted by the question, which says there are exactly 4 dogs named Jeff.

Because the third dog's statement cannot be true, the third dog is lying .

The first, third and fifth dogs all refer to the first dog. Since the first and fifth say the same thing, they are both honest. The third dog says that the first dog is lying, and thus it is the third dog who is lying.

You only need to look at the first three dogs' statements. If the first is lying, then the second is telling the truth, which would make the first two non-Jeffs, contradicting the problem statement. Hence the first dog is telling the truth, thereby exposing number 3 as the liar.

If Christopher Boone met these dogs, it would change his view of them forever!

I think I found a problem in this problem: If the third dog is lying, then that means that: The first dog named Jeff is telling the truth, and the second dog is lying. But then that makes the second dog also not truthful, and therefore we have 2 dogs which are lying. The question states that there are only exactly one dog lying, thus the solution is false. Unless the third dog is only telling half the truth? I think the question needs to clear up on that one.

First, I looked at the dog's who's comments were definite, the first one being the 4th dog, who says that one dog is definitely not Jeff. Now, looking at the first three dogs, we can see that the 1st one would be changed to "anti-jeff" and the 2nd one would stay the same according to the 3rd. But, a problem arises when tallying these values following the rule from the 3rd dog getting us: 1st = not Jeff 2nd= not Jeff 3rd= Jeff 4th= Jeff 5th= Jeff Adding these up does not agree with the prompt: "...there are exactly 4 named Jeff." So, in conclusion we just say that the 3rd dog is messing it all up and that is the answer.

By reading all the dog statement, and using the analogy whereby only one dog can lies.

2 statement can’t contradict with each other

In conclusion:

4th dog (Truth) 1st and 5th dog (Truth), if it is false, contradiction happened and lastly, 3rd dog is lying because if it is true, 1st and 2nd dog statement will contradict each other.

Here are three related ways to think about it; they all reach the correct answer:

FIRST WAY

Look for two contradictory logical statements. Since there is by definition only one liar, one of the contradictory statements must be TRUE and other FALSE. If there is a contradictory pair, all other statements can be assumed TRUE. Use these other TRUE statements to decide which of the two contradictory statements is actually True.

In this problem: Dog 3 claims that neither Dog 2 or Dog 1 are named Jeff, implying that the number of dogs named Jeff is 3 or less. Dog 4 claims that there are exactly 4 dogs named Jeff. Thus, Dog 3 and Dog 4 cannot both be telling the truth. One is definitely making a FALSE statement. Because we know there is only one liar, and it must be Dog 3 or Dog 4. We can trust dog 5 to break the tie. Dog 5 says that Dog 1 is Jeff, which proves Dog 3 was not telling the truth.

SECOND WAY

We can see that Dog 3 is contradicted by Dog 4 and Dog 5. Any dog contradicted by more than one other dog must not be telling the truth in a one-liar scenario.

THIRD WAY

• The problem states only one Dog can be False.

• Suppose Dog 3 is True it implies {(Dog 4 is False) AND (Dog 5 is False)}

• Therefore two dogs are false, which contradicts the premise.

• By contradiction, Dog 3 is not TRUE, he is the liar.