Join squares 2
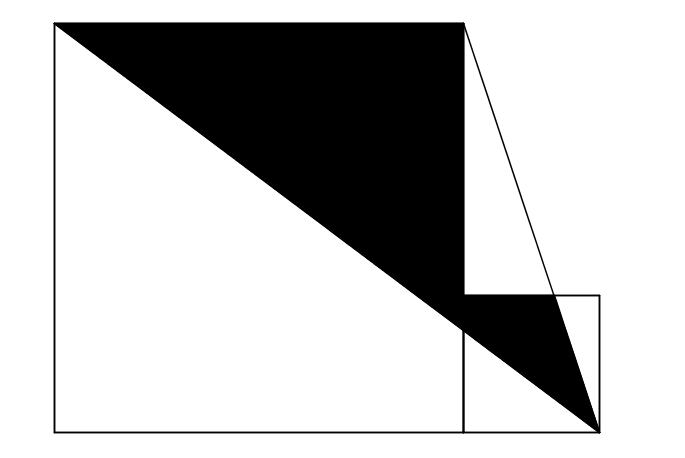
The figure above shows two squares of sides 9 and 3, respectively. Find the area of the black region.
The answer is 34.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice solution +1..did it in a similar way. I found the area of the two regions separately, then added them to get the ans. as (69/2). I found the area of the smaller region by subtracting the areas of triangle IDE & CHJ from the triangle CDE ( referring to your figure). Yet ur method is simple and nice.!
Nice solution!. Where did you draw the image?
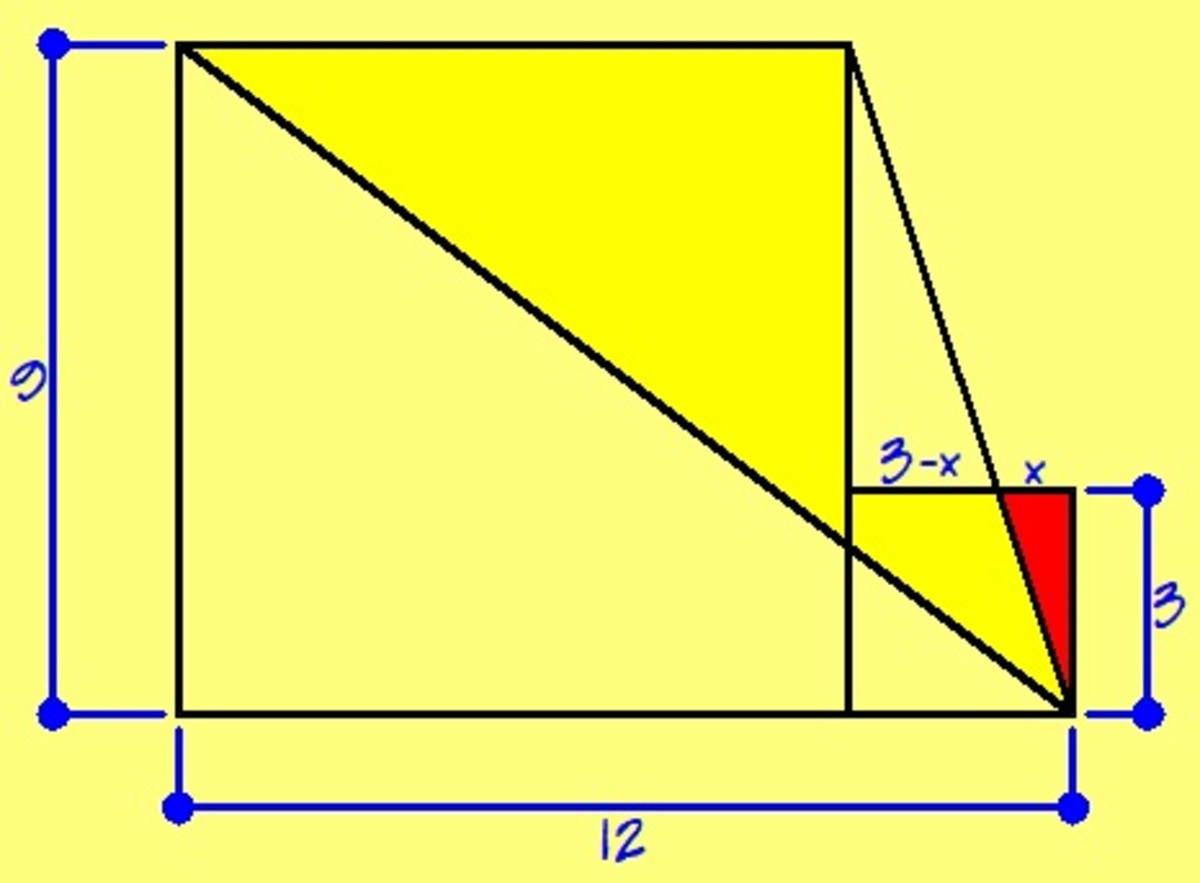 Consider my diagram. The area of the shaded region is area of the two squares minus area of the big triangle minus area of the red triangle.
Consider my diagram. The area of the shaded region is area of the two squares minus area of the big triangle minus area of the red triangle.
By similar triangles, we have
3 x = 6 3 − x ⟹ x = 1
The desired area therefore is
A = 9 2 + 3 2 − 2 1 ( 9 ) ( 1 2 ) − 2 1 ( 1 ) ( 3 ) = 3 4 . 5
This is my own solution. I deleted my account and I am using a new account now.
Credit to Sambhrant Sachan for the image
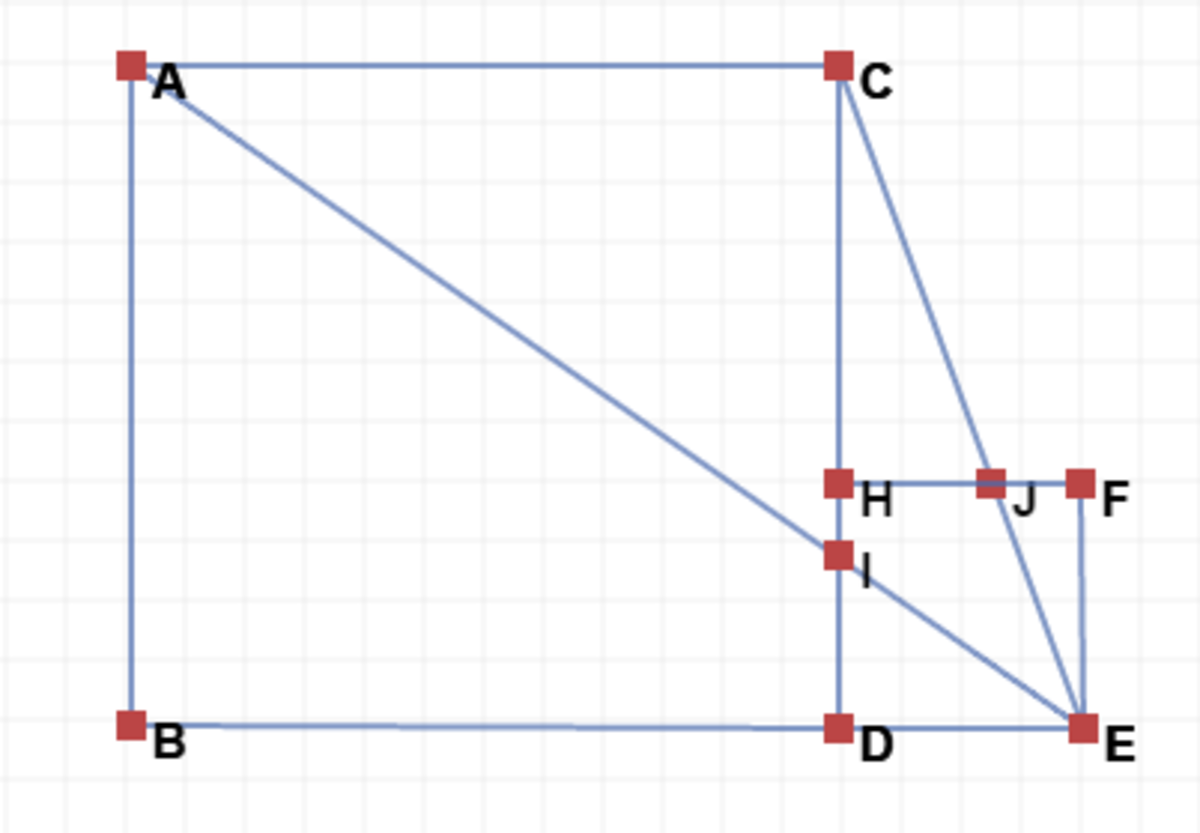
The key is to express the black area (let's call it β ) in two different ways. Let H J equal x .
β 1 = A C E − C H J = 2 A C × C D − 2 C H × H J = 2 8 1 − 6 x
β 2 = A B C D + D E F H − A B E − E F J = A C 2 + D E 2 − 2 A B × ( B D + D E ) − 2 E F × ( 3 − H J ) = 3 6 − 2 9 − 3 x
Set the two equations equal to each other.
β 1 = β 2 2 8 1 − 6 x = 3 6 − 2 3 − 3 x 8 1 − 6 x = 7 2 − 9 + 3 x ⟹ 1 8 = 9 x ⟹ x = 2
Now plug x back into one of our original equations for β
β = 2 8 1 − 6 × 2 = 3 4 . 5
nice solution .. +1
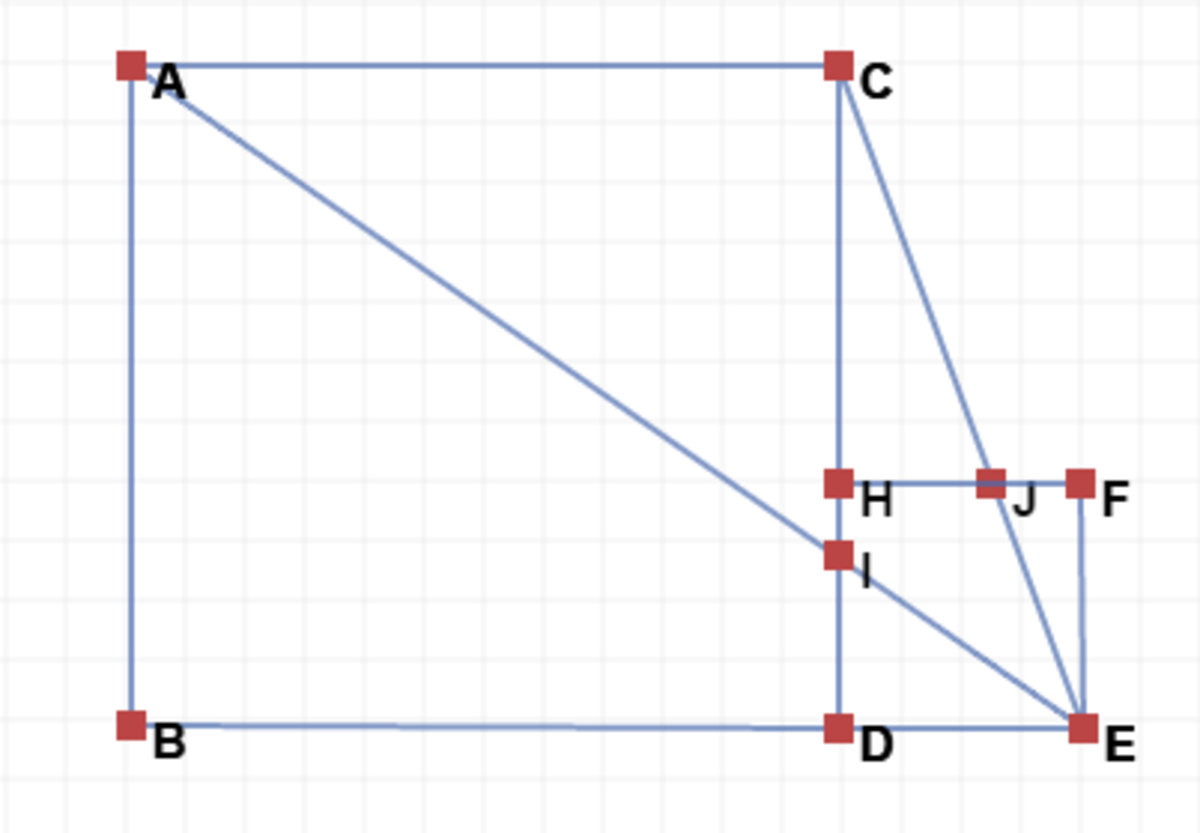
Using this image, (credits to Sambhrant Sachan), we will first find the area of Δ A C E . But this is simply 4 0 . 5 by the area of a triangle formula. Now, we will find the area of Δ C H J . Note that Δ C H J ∼ Δ J F E in the ratio 2 : 1 . From this, we get the length of J H to be 2. From this, we get that the area of C H J is 6. Thus, the area of A C H J E = ∣ A C E ∣ − ∣ C H J ∣ = 3 4 . 5 . Thus, the answer is 3 4 . 5 .
nice solution.. +1
How did u get the area of ace triangle. U only know the base as 9. How did you calculate the height??
Log in to reply
The height is also 9, because A C ∥ B E .
Log in to reply
Sorry for bugging u again n again
But u see CE is the height of the concerned triangle but it is also the hypotenuse of triangle cde. So by Pythagoras ce is underroot of 90.. Which is not 9.. Then how come it is explained as 9..
Log in to reply
@Aditya Dev – No. The height has to be perpendicular to the base. As you can see, C E is not perpendicular to A C , so it isn't the height.
A r . o f △ A C E = 2 1 × 9 × 9 A r . o f △ C H J = 2 1 × H C × H J , Where H C = 9 − 3 = 6 To calculate HJ , Let ∠ C J H = ∠ C E D = θ tan θ = 3 9 = H J H C ⟹ H J = 2 Answer = 2 8 1 − 2 1 2 = 3 4 . 5