Just arithmetic
An arithmetic progression consisting of n terms which are alternatively odd and even has its first term a an odd positive integer and common difference d also a positive integer.
When the sum of the first, third, fifth, seventh, ... terms are subtracted from the sum of the second, fourth, sixth, eight, ... terms, the result obtained is 501. Find n × d .
The answer is 1002.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Well, maybe − should be substituted by 2 n , right?
Log in to reply
For which line are we talking about?
Log in to reply
Log in to reply
Log in to reply
@Abhay Tiwari – Woah, a bug!!! Remove the image from your solutioh, it makes it look wierd XD
Log in to reply
@Ashish Menon – Sometimes this site behaves abnormally. It gets on my nerve. For instance, that pic I wanted to upload for replying you. And it is now stuck there like a vaccum pump.
Log in to reply
@Abhay Tiwari – Haha, yeah true. It happens that the page reloads a lot of time erasing away all the work I did even if it was a huge one and I have to do it all over again. -.- :P
Log in to reply
@Ashish Menon – Many a time I post a question, and my previous question gets posted with the answer of my new questions. And that is really weird. Make me feel like I am goofing around here XD
@Abhay Tiwari – Hmm.. nice solution(+1)
This AP starts with an odd positive integer and its term are odd and even alternatively. So, we can comment that the common difference is odd. Now, the difference between the sum of the even numbered terms and the sum of the odd numbered terms is 5 0 1 indicating that the sum of the even numbered terms is greater than the sum of the odd numbered terms. Since, these terms are in AP of alternating even and odd terms, we can comment that this AP ends with an even number. This is because if it was ending with an odd number then the sum of the odd numbered terms would have been greater than the sum of the even numbered terms. Since this AP ends with an even number, we can comment that the number of terms in this AP is also even because this AP of alternating odd and even numbers start with an odd positive integer.
So, the number of odd numbered terms = number of even numbered terms =
2
n
.
Sum of odd numbered terms =
2
×
2
n
×
(
a
+
a
+
(
n
−
2
)
d
)
=
4
n
×
(
2
a
+
n
d
−
2
d
)
.
Sum of even numbered terms =
2
×
2
n
×
(
a
+
d
+
a
+
(
n
−
1
)
d
)
=
4
n
×
(
2
a
+
n
d
)
.
Sum of even numbered term - Sum of odd numbered terms =
5
0
1
.
(
4
n
×
(
2
a
+
n
d
)
)
−
(
4
n
×
(
2
a
+
n
d
−
2
d
)
)
=
5
0
1
4
n
×
(
2
a
+
n
d
−
2
a
−
n
d
+
2
d
)
=
5
0
1
n
×
2
d
=
2
0
0
4
n
d
=
2
2
0
0
4
n
×
d
=
1
0
0
2
The common Difference will be odd not even..Please see to it.. And I don't understand one thing.. How is sum of even numbered terms = n(2a+nd)/4? I mean S = n/2 × [2a + (n-1)d].. And n will be equal to n/2.. So how will it be equal to n(2a+nd)/4? Same confusion goes for odd numbered sum..
Log in to reply
I saw into it, the common difference is odd and not even XD I edited it. Anyways its of no use. If we are considering only even numbered term, there are
2
n
right. Now the first even number is
a
2
=
a
+
d
because it starts with an odd positive integer. Since this AP have alternating odd and even terms, the second term would be even. The last term is even as proved in the solution. The last term of the original sequence can be written as
a
+
(
n
−
1
)
d
. Now, sum of even numbered terms =
2
Number of even numbered term
×
(
First term + Last term
)
=
2
×
2
n
×
(
(
a
+
d
)
+
(
a
+
(
n
−
1
)
d
)
)
=
4
n
×
(
2
a
+
n
d
)
Same reply goes for odd numbered terms.
Yes numbered of terms is 2 n but we have to divide by 2 again as in the formula. You didnt do that. Hope this satisfies... :)
Again going by your formula:- For even numbered terms n in all places would be substituted by 2 n . a would be substituted by a + d . And d would be substituted by 2 d . Be careful with that one.

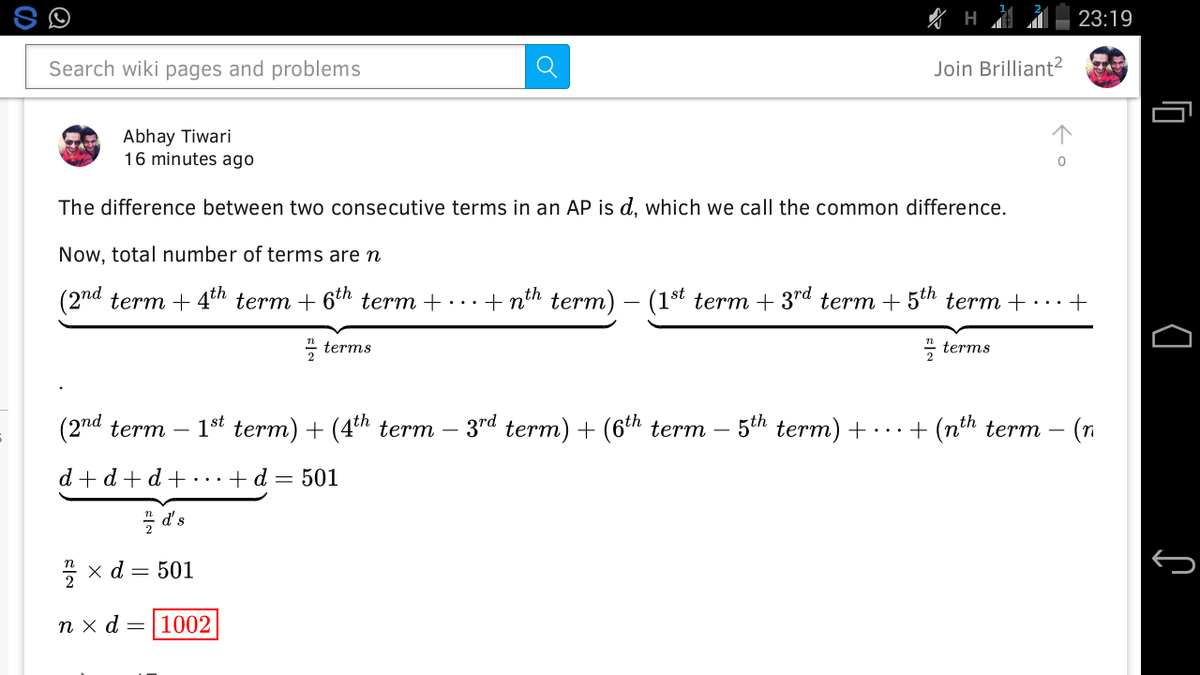
The difference between two consecutive terms in an AP is d , which we call the common difference.
Now, total number of terms are n
2 n t e r m s ( 2 n d t e r m + 4 t h t e r m + 6 t h t e r m + ⋯ + n t h t e r m ) − 2 n t e r m s ( 1 s t t e r m + 3 r d t e r m + 5 t h t e r m + ⋯ + ( n − 1 ) t h t e r m ) = 5 0 1 .
( 2 n d t e r m − 1 s t t e r m ) + ( 4 t h t e r m − 3 r d t e r m ) + ( 6 t h t e r m − 5 t h t e r m ) + ⋯ + ( n t h t e r m − ( n − 1 ) t h t e r m s ) = 5 0 1
2 n d ′ s d + d + d + ⋯ + d = 5 0 1
2 n × d = 5 0 1
n × d = 1 0 0 2 !