Just Cancel?
Solve for
x
:
x
−
1
x
=
x
−
1
1
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Moderator note:
I'm glad that most people recognize the need to check for extraneous answers. These arise when we multiply by 0 (e.g. cross multiplying in this solution), squaring terms, combining non-linear equations, and more.
Bear this in mind as you work on harder problems, like March 27 Advanced . Do not forget your basics.
It may not be defined; but we were asked if it were equal. It is EQUAL !!!
Log in to reply
If 0 1 = z , then it means 0 z = 1 , but there is no real number z for which this equation is true. This means that 0 1 is not defined, it doesn't exist, it has no meaning. Sure, both the LHS and the RHS look similar, but if they don't exist, then can we say that they are equal?
Log in to reply
cross multiply and get (x-1)^2 = 0, x = 1, 1. The fraction x/0 or 1/0 may be undefined, but x is 1 regardless of what the denominator is. You do not have to cross multiply; if the denominators are equal, and the two expressions are equal, the numerators are equal. x =1.
Instead of trying to cross multiply, we could begin by assuming that x − 1 = 0 and then cancel the denominator to arrive at a contradiction.
Saves you the trouble of having to go through the cross multiplications.
Log in to reply
That's in fact the most adequate solution if you admit we are talking about real numbers.
No need to assume - from the claim that something equals x − 1 1 we /know/ that x − 1 = 0 .
I don't understand how 1/0 = 1/0 is undefined.
1/0 by itself is undefined, but 1/0 = 1/0 is true because both sides of the equation are of the same form. The only value for x for which this happens is when x = 1. Is that not correct mathematically? Semantically it is.
If you graph both sides, they intersect at y = infinity as x approaches 1 from x>1 and - infinity as x approaches 1 from x < 1.
Log in to reply
No.. undefined cannot he equated as you are saying. They are not equal.
Well, not exactly. You can't just say the equation reduces 1/0 = 1/0 at x = 1, and thus x = 1 is a solution. This is because the expression "1/0" (as written) is undefined. One must examine how the LHS and RHS terms scale with each other as the denominator approaches zero. For example, consider the equation:
1/(x-1) = x/(x-1)^2
At x=1, this reduces to 1/0 = 1/0. However, in this case x = 1 is NOT a solution. You can see this by cross multiplying, yielding:
x-1 = x
which has no solution (x approaches infinity). This is because 1/(x-1)^2 approaches zero much faster than 1/(x-1).
However, going back to the original problem, we can say that the LHS and RHS both scale as 1/(x-1). Thus by simply multiplying both sides by x-1, the equation reduces to x = 1. So it has a solution.
Several people responding to this forum are confusing limits (a calculus concept) with substitution (an algebraic concept). Yes, it's true 1/0 is undefined. But the limit of 1/x as x->0 is well defined.
why did he not just multiply by x-1 instead of cross multiplying?
So 1/0 is undefined because zero is a non-existent number we use only to state that no number is there, making everything thus disappear because 1 of nothing is nothing?
Log in to reply
No.Zero is a number. We do this for multiple reasons, such as this:
Let a=b a^2=ab a^2-b^2=ab-b^2 DIVIDE BY A-B a+b=b Since a=b: 2b=b b is non zero, so: 2=1 Notice the error. This is called the zero proof and is one of the many reasons why we can not divide by zero, rather only use limits. We treat zero as a number in all other causes and mathematicians even treat x/0, provided x is not zero, as the concept of plus or minus infinity. But 0/0 is undefined, there are infinitely many solutions(1, 2...)
but if we multiply each side by (x-1) surely the result will be x=1. The (x-1) on the numerator and demoninator on both sides of the equation must surely cancel each other other out to 1 . x = 1. 1? i.e. x=1
Log in to reply
but of course if we substitute x for 1 in the original equation we will still get 1/0 = 1/0 i.e. undefined.
Yes. Correct.
Hi Calvin, is there anything that can be done about the glitch I talked about?
The answer posed to this problem by Mr. Zuhair is erroneous. The correct solution is x =1. The fact that specific terms in the equation become singular at x = 1 is irrelevant, provided they scale together. This can be seen simply taking the limit of both terms as x-> 1. LHS approaches 1/(x-1), while RHS also approaches 1/(x-1). So clearly x = 1 is a solution.
I had it right the first time (I know -everyone says that). Just by glancing at it, you see an imbalance, therefore no solution. But I do enjoy reading all the drawn-out explanations by the math whizzes in the group. I am new to this assemblage of detail-oriented folks, and I am by no means good at math, but now at 57 yrs old, lately I have been enjoying the feeling of comprehending an equation I didn't know when I was in high school. I tend to think that this group doesn't believe that knowledge-gathering stops after formal education. We are as humans, programmed to be inquisitive. To learn "stuff" from birth until death, even if you can't categorize it in any formal book of knowledge. And that natural drive shouldn't ever be stymied, whether from an educational system or the current assault on intellectuality. (Give me a break- what is an "alternative fact" Mrs. Conway?). It is good and righteous to question everything. Just scratch and delve just below the surface. You just might find a jewel or water. Whatever you need. Like for me, I just read that LIGO just confirmed the third detection of a gravitational wave, confirming Einstein's theories. Effing beautiful! Now we know the buggers exist. Now it's up to you physicists/mathematicians to sort the info out and make some beautiful noise with the Unified Field Theory, and any implications it may have with M-Theory, and String Theory.
Please pardon my digression for today I'm on a roll.
Fun!! I haven't thought much about math since high school (50 years ago). But I do remember that dividing by zero is undefined. So is it cheating to multiply both sides of the equation by x-1 to rewrite the equation and take zero out of the denominator?
x^2 - 2x + 1 = 0
This is clearly solved by x = 1.
What law of the universe did I transgress? Will the Trump Justice Dept prosecute (if it can figure out that x is an unknown - known or unknown)?
:o)
Log in to reply
Hi Adam. The problem with this is that you have multiplied both sides of the equation by (x-1)^2, so you've introduced x = 1 as a solution.
For example, let's say the original equation was x/(x-1) = 3/(x-1). Now cross multiply. You'll get a quadratic equation with two solutions: x = 1, x = 3. But this does not mean x = 1 is a solution to the original equation.
What you can say is that the functions 1/(x-1) and x/(x-1) approach equality in the limit of x->1. So from an engineering standpoint (I am an engineer), we would often look at a problem like this and say that x = 1 is a solution from a practical standpoint. The mathematicians on this forum argue otherwise.
You cannot "multiply by 0 (even artificially)". This gives us implication in one direction and not the reverse direction.
As an extreme / obvious example, if we wanted to solve x = 0 , we cannot say "Let's multiply both sides by ( x − 1 ) to get x ( x − 1 ) = 0 , and conclude that " x = 0 or 1". Explicitly, x = 0 ⇒ x ( x − 1 ) = 0 , and it is not true that x = 0 ⇔ x ( x − 1 ) = 0 .
This is why it's important to know what kind of implication signs you have. When doing addition and subtraction of linear equations, we often have double implication signs. However, this might not be the case when we start to multiply, square, add quadratic terms, etc.
First step is multiply both sides by X - 1 instead of the bizarre way that you did it this van simplifies equation to x equals 1
Log in to reply
Remember that you are only allowed to multiply both sides of an equation by a non-zero number. When "x equals 1", then "x-1 equals 0" and so we do not reach the desired conclusion.
Log in to reply
That is not strictly correct. Multiplication by zero is perfectly valid - it's just a special case of x = y ⇒ f ( x ) = f ( y ) , which is the basic principle on which we rely when we do something to both sides of an equation. In this instance, the result is always 0 = 0 . So it's a useless transformation, but still a valid one. If we multiply the given equation by x − 1 , then the result is ( x − 1 ) x − 1 x = ( x − 1 ) x − 1 1 . What we cannot do is cancel out the x − 1 terms on each side, unless we're sure that x = 1 .
Log in to reply
@Stewart Gordon – Thinking about it now, since division by 0 is undefined, the equation essentially says that x = 1 . So on this basis, we can deduce x = 1 by cancellation of the multiplication and division. However, this only means that x = 1 if the original equation is true. But we have also deduced that x = 1 . Thus we have a contradiction, thereby proving the original equation to be necessarily false.
@Stewart Gordon – Right. What I meant to convey is "When you multiply both sides of an equation by 0, then solutions to the second equation need not be solutions to the first equation." Multiplying both sides of an equation by 0 would make all values a solution in the second equation, but clearly that need not be the case for the first equation.
When solving equations, what we're generally after, is if and only if ⇔ implications. When we only have a one-sided implication, e.g. if ⇐ in this case, then we have to verify that we didn't introduce extraneous solutions. The most common examples of this is that x = y \Rightarrnow x 2 = y 2 , where we know we have to "verify that we didn't introduce an extraneous solution when squaring".
Unfortunately, most places teach this as an afterthought and do not make it explicit why / how this is important. This leads to misconception errors like the one above.
x − 1 x = x − 1 1
<--> x − 1 x - x − 1 1 =0 <--> x − 1 x − 1 =0 but x − 1 x − 1 =1 and 0≠1 Therefore there would be no solution
Note that x − 1 x − 1 = 1 only when x = 1 .
No! The functions f(x) = 1/(x-1) and g(x) = x/(x-1) approach each other as x approaches 1. x = 1 is a solution.
Log in to reply
Functions approaching each other does not mean that they are equal at that point.
There is no solution to that equation, since substituting in x = 1 makes it undefined.
Log in to reply
Not in all contexts. Singular equations can have solutions, even at the point where they are singular. In this example, consider a singular perturbation expansion using the variable s = x-1, then examining the LHS and RHS as s approaches zero. We would have:
(1/s) (1+s) = (1/s) (1)
As s approaches zero, both terms scale as (1/s), and thus we must remove this dependence and examine the multiplying series:
1 = 1 + s
As s approaches zero, these terms become equal. Thus x = 1 is a solution. The fact that both RHS and LHS diverge to infinity is irrelevant.
If confused about this, I urge you to read up on singular perturbation theory and its applications. This problem, and its solution should be removed from this module as it adds nothing to a deeper understanding of algebra, and sows seeds of confusion for students studying power series and other more advanced algebra and pre-calc concepts.
Log in to reply
@Rel Dauts – The context of this problem is pretty clear: solve the equation as given. No mentioning of limites, continuations of functions with singularities etc. Just a simple equal sign. As there is no x that yields the same defined result on both sides, this equation is not solvable.
Higher mathematics often uses very simplified notation that, unfortunately, often is ambiguous, so the context is needed to understand which meaning of the notation is intended. E.g. the null vector often is written as "0",the same as the scalar "0", though it is no scalar. In "singular perturbation theory" the notation of an equation might be a defined shortcut that includes "reasonable" continuations (i.e. with defined limites). Without that context, an equation is an equation.
I'd like to officially flag this problem for offline discussion. This problem lacks adequate context, and I think the author needs to rethink its purpose, perhaps finding a less ambiguous way to illustrate the same point.
Log in to reply
@Rel Dauts – The problem is fine as stated.
You are assuming that "just because the function looks that way in the limiting sense, it has to behave in that way", which is not valid for solving equations.
Always remember that when manipulating equations, you might introduce extraneous solutions, especially when you 1) multiply by zero, 2) square terms, 3) add/subtract non-linear equations.
Log in to reply
@Calvin Lin – I think that's a bit of an oversimplification of the issue here. Much of 19th century mathematics was dedicated to finding solutions to ODEs that have singular terms in them. This led to many of the series functions we know today (e.g. Bessel series).
Just as a simple example, consider the equation:
sin(x)/x = 1.
If I follow your arguments correctly, this equation would have no solution. But it does: at x = 0.
To understand this, we must re-express sin(x)/x in a power series around x = 0. This approach was commonly used to find solutions to ODEs near ordinary points. These methods were later extended to regular singular points by dividing out the offending singularity common among terms.
As I understand your motive here, your goal is to insure students don't introduce extraneous solutions by manipulation. I get that. But this is a flawed illustration of that point. If the students cross multiply, they get a quadratic with a double root at x = 1. But they only introduced one of these, the other was already there.
Perhaps it would help to consider a specific physical example that obeys your original equation. Consider a damped harmonic oscillator with governing ODE:
y" = -2 k y' - y
Assuming a general solution y = exp(-r*t), we can solve for two roots. The resulting algebraic equation can be put in the form:
(r-r1)(r-r2) = 0.
where r1,r2 = k ± sqrt (k^2-1). Now let's say we manipulate into one of two forms:
r/(r-r2) = r1/(r-r2). r/(r-r1) = r2/(r-r1).
Based on these two forms, we can (separately) conclude that r = r1 and r = r2 are solutions. They also must remain valid solutions, even if r2 becomes vanishingly close to r1, and these two particular forms become singular. i.e. there is no discontinuity in physical behavior as these roots cross - there is a smooth transition from underdamped to overdamped response as k crosses through 1. Often, equations have context, and if you lose sight of that context, it is easy to draw the wrong conclusion.
This leads to my final suggestion, which is to re-wite the problem in a way that retains the point you want to make, but does not invite criticism from professors of advanced calculus for engineers! Replace the removable singularity in your equation with one that forces the two terms to diverge in the limit of x->1 rather than converge as they do now. This will better support your point that numerical agreement cannot be established at a singularity, while not inadvertently (and incorrectly) implying that equations with singularities in them cannot be solved.
Log in to reply
@Rel Dauts – There is indeed no solutions to x sin x = 1 . It is indeed true that lim x → 0 x sin x = 1 . These 2 statements are not contradictory.
There is a huge difference between talking about the value at a point, and the limit of the value at that point. You claim that "professors of advanced calculus for engineers" do not make that distinction, which might be true if they are looking at the general behaviour of the function, or have made the additional (unwarranted) simplifying assumption that the function is smooth.
When dealing with a basic scenario, it is not ideal to reference "high power mathematics". This is because certain assumptions might have been introduced in the theory that deals with these specific cases. For example, in calculus, it is established that the sum 1 + 2 + 3 + 4 + … diverges to infinity. However, there are "high power applications" in which we interprete the summation in as an analytic continuation of a certain series, and thereby obtain the value of − 1 2 1 .
Log in to reply
@Calvin Lin – Your problem does not make it clear one way or the other whether you are talking about limiting behavior, or the numerical value at a point. You just say "solve for x." In my mind that leaves it up to the reader to fill in the context. I am trying to show you there is a context (a common, practical, and not at all obscure) context in which x = 1 can be considered a solution.
I will soften my stance in some of these posts. However, I maintain that you should change the problem is such a way that the context doesn't matter to the point you are trying to make, or to provide more explicit context (e.g. "find the roots of f(x) = 0, where the real function f(x) = x/(x-1) - 1/(x-1)."). Otherwise you are just inviting reader confusion, and/or long and somewhat painful debates about the meaning of the problem (like this one!) Is your objective to be right, or to interest and enlighten readers?
That reminds me of a joke. A physicist, a chemist, and an engineer are traveling together in a hot air balloon, and get lost in a fog. They yell toward the ground hoping to raise someone's attention, screaming for hours "Where are we?, Where are we?" Finally they give up and sit back down in the balloon to wait it out. Finally, just as the fog starts to lift and they can tell where they are, a faint lone voice calls from the ground: "You're lost!"
The engineer rolls his eyes and says to the others "That guy must be a mathematician." the physicist says, "How do you know that?" The engineer replies "because his answer took a really long time, was elegantly simple, absolutely correct, and completely useless."
by symmetry x =1 but this leaves a denominator of zero so there can be no solution
Why did you even consider x = 0 in the first place?
Log in to reply
Because it was given as a possible answer. When you eliminate all the possibilities, the last one remaining, however improbable, will be the correct one, at least according to Sherlock Holmes :)
Your mathematical logic defies my eyes and common sense. I choose to be obstinantly and proudly incorrect. Clearly when 1 is substituted, the left side matches the right.
Log in to reply
If you substitute x=1 into the equation, you will get LHS = 1/0, which is undefined, same goes for RHS. Just because both LHS and RHS are undefined, that doesn't make LHS = RHS.
On the other hand, using your logic, we can claim that 1/0 = 2/0, so 1 = 2.
You can't just substitute x->1, since 1/0 is undefined. But you CAN multiply both sides by (x-1), leaving x=1 as a solution. I suspect the author of the problem was trying to make this point, but failed to have the two denominators scale differently with x. A better illustration would be the equation:
1/(x-1) = x/(x-1)^2.
This has no finite solution (x = infinity), even though substitution x->1 yields 1/0 = 1/0.
Log in to reply
You can multiply both sides by (x-1) ONLY if (x-1)≠0 ⇔ x≠1. Therefore the seeming solution x=1 is in contradiction to this condition and is invalid.
Under the rules of algebra, you cannot divide by 0. If you use limits in a more calculus based approach, you could argue that x=1 because even though you cannot divide by 0... as you approach 0 [without actually reaching it when x=1] it works. From an engineering perspective, the surrounding practical application that provided this problem would help as well to better determine if this can be solved as [x=1] or not..
Given the problem (x-1)^2 = 0 and asked to solve for x, we readily obtain x = 1 as the only solution. Let's work the problem backwards...
(x-1)^2 = 0
x^2 - 2x + 1 = 0
x^2 - x - x + 1 = 0
x(x-1) - (x-1) = 0 At this point would we still agree that x = 1 is the solution?
x(x-1) = x-1 How about now, is x = 1 still the solution?
Now let's divide both sides by (x-1)^2 ...
x(x-1)/(x-1)^2 = (x-1)/(x-1)^2
x/(x-1) = 1/(x-1)
...and in doing so, we magically turn a problem with a solution into one without a solution. In this case the problem is made "messy" by dividing by an variable term.
In the original problem, the "messy" problem is made "clean" by eliminating the variable term in the denominator, and thus the answer is should be x = 1.
Log in to reply
If x = 1 , then ( x − 1 ) 2 = 0 , but you cannot divide both sides of the equation by 0, so your logic is flawed.
F ( x ) = x − 1 x − x − 1 1 Now we need to find roots F ( x ) = 0 , but F ( x ) = 1 ∀ x ∈ R − 1 So there must not be a solution.
Sorry, but I think in this case, F(x)=1, so it's not the same situation...
Log in to reply
F ( x ) = 0 is something to be solved whereas you already know F ( x ) is a constant function. For example if we are to solve sin x = 2 then we see that if F ( x ) = sin x − 2 then we need to solve F ( x ) = 0 but F ( x ) ∈ [ − 3 , − 1 ] which clearly rules out any possibility of solution.
Log in to reply
Thanks, friend. I understand your approach now... :)
The issue is not whether F(x) = 0 has a solution. The issue is whether the roots of F(x) = 0 (where F(x) = LHS - RHS) correspond to the solutions to the original problem. They don't, because LHS and RHS are both singular where RHS = LHS.
Another example would be exp(x)/x = 1/x. If we define F(x) = (exp(x)-1)/x, there is no root at x = 0, even though x = 0 is a solution to the original singular equation. We're not creating a solution by multiplying by x. The solution is there already because exp(x) = 1 at x = 0.
Log in to reply
@Rel Dauts – x e x = x 1 doesn't have a solution either ways at x = 0 . Defining a function is appropriate here until you really make some arrangements and modifications. You cannot multiply x throughout
Log in to reply
@Aditya Narayan Sharma – Sure you can. The solution at x = 0 does not come from multiplying both sides by x. It comes from the fact that exp(x) = 1 at x = 0. Get a computer and make a plot of exp[x]/x and 1/x for -epsilon < x < epsilon. Then make epsilon smaller and smaller and see what happens! You'll see that these functions become very large, but identical, as x approaches zero.
You can't conclude that two singular functions are unequal at the singularity solely because they are singular. You have to compare terms of equal order in x.
Log in to reply
@Rel Dauts – Okay let me explain, the equation doesn't have a solution just because it makes both sides indeterminate and according to you this very equation (the problem we are commenting on) has x = 1 has a solution. But it isn't because it makes the expressions indeterminate.
Log in to reply
@Aditya Narayan Sharma – Yes, the expressions (RHS and LHS) are numerically indeterminate at x = 1. So F(x) as you define it does not have a root at x = 1. However, this does not mean these terms are mathematically undefined as x approaches 1. [Edit: In my opinion the original problem leaves it unclear if we are finding the roots of F(x) = LHS-RHS, or solving for a limiting value of x at which RHS = LHS].
Consider the expression x/sqrt(x) as x->0. As written it is 0/0 at x = 0. But it's dependency on x is clear, so it can be compared to other terms that also scale with x in some way as x->0. For example, which of the following terms is bigger as x approaches zero?
x or sqrt(x)?
Both terms are equal to zero at x=0. But does that mean these terms become functionally equivalent as x approaches 0? No! sqrt(x)>>x as x->0.
One can examine singular terms the same way. For example, which of the following terms is bigger as x approaches zero?
1/x vs. 1/sqrt(x)?
As I understand your argument, these terms are both 1/0 at x = 0, and thus undefined, so it's impossible to know which is larger. But in many important mathematical contexts this is a misleading conclusion. 1/x is much larger than 1/sqrt(x) as x approaches zero. Thus we can say that in the limit of x->0, 1/x >> 1/sqrt(x). likewise, in the limit of x->1, 1/(x-1) = x/(x-1).
Let's take a step back. As I understand it, the point of this problem is that simple substitution of x = 1 into the equation yielding 1/0 = 1/0 is inadequate to prove that x = 1 is a solution. I get that. So how about re-writing the problem such that the equation is:
x/(x-1) = 1/(x-1)^2.
This clearly has no solution at x = 1, since the two terms scale differently with (x-1). This retains the algebraic instructional value of the problem without being inconsistent with concepts of calculus that students will later be asked to understand.
No! You can't just write as F(x) = LHS - RHS and then search for roots of F(x). This is because LHS and RHS are both singular (go to infinity) where RHS = LHS. Thus there is no guarantee that F(x) will have a root where RHS = LHS.
A better approach is to define G(x) = LHS/RHS - 1. This divides out the underlying singularity. In this case, G(x) = x/1 - 1, which has a root at x = 1.
That's a nice approach :)
The quantity (x-1)/(x-1) is only equal to 1 for values of x not equal to 1. For x = 1, (x-1)/(x-1) = 0/0, which is undefined on an absolute basis. So you can't conclude there is no solution at x = 1 from this. You have to resolve the singularity first by multiplying by x-1. Then the difference between the LHS and RHS has meaning.
Note that when you multiply both sides by x-1 you generate a new root at x=1. But you end up with a quadratic equation that has a double root at x = 1. So, although you introduced one of these roots by cross multiplying, the other root represents the solution to the original (singular) equation.
x − 1 x = 1 + x − 1 1 ⇒ 1 + x − 1 1 = x − 1 1 ⇒ 1 = 0 (CONTRADICTION)!
Not only is 1/0 equal to 1/0; they are identical !!! The question WAS are they equal, not do they exist.
Log in to reply
1/0 = 1/0 is definitely not true. Just because 2 expressions are undefined, that does't make them equal to each other.
Log in to reply
Agree. One cannot conclude that the LHS and RHS are equal at x = 1 simply by substitution, and saying 1/0 = 1/0. However, one can examine how each term scales with x as x approaches 1. Since both LHS and RHS scale as 1/(x-1), we can look at the numerators to see where these terms will be equal. This yields a solution at x = 1 (even though both terms are going to infinity) because they both merge to the same very large value as x approaches 1.
Not a contradiction at x = 1. This is because as x approaches 1, the quantity 1/(x-1) goes to infinity. So what you are actually looking at is:
1 + infinity = infinity,
which is not a contradictory statement. It's only contradictory for x not equal to 1.
Log in to reply
No, we are substituting the exact value of 1 to see if it's a solution of the given equation. We are not substituting values close to 1.
Log in to reply
You are missing my point. I agree that substitution of x=1 into the equation is inadequate to show that x=1 is a solution. But lack of proof for a conclusion is not proof that that conclusion is incorrect. In this case the RHS and LHS approach each other mathematically in the limit of x approaching 1. So it's a solution (singular though it may be).
Imagine ANY equation of the form LHS=RHS with non-singular root at x=1. Now divide both sides by (x-1), making each term singular. You seem to be saying that x=1 is no longer a solution to the revised equation. No, you've just masked the solution beneath a singularity. You must remove this singularity by multiplying both sides by (x-1) to reveal this underlying solution.
Log in to reply
@Rel Dauts – So, if x - 4 = 0, then (x-4)(x-1) = 0 as well, so the solution of x are 1 and 4 (because we multiply both sides by (x-1))?
Log in to reply
@Pi Han Goh – No. You created the x=1 solution by multiplying by (x-1). But x=4 is still a solution even after multiplying by x-1.
Let me provide another example. Solve sin(x)/x = 1. If I follow your logic correctly, there is no solution.
Log in to reply
@Rel Dauts – So there's no solution for (x-1)/(x-2) = (x-2)/(x-1) because we multiply both sides by (x-1) and by (x-2) to remove the singularities, correct?
Log in to reply
@Pi Han Goh – Not sure I understand your point. Here the two terms do not share the same singularity, so there is no way to remove. This has a non-singular solution at x = 1.5.
The denominators are the same, so the numerators must be equal, so x equals one. However, because the denominator cannot equal 0, which you would get by plugging in one for x, the answer is no solution.
Subtract x − 1 1 from both sides giving 1 = 0 to show the expression is false and has no solutions.
Very sneaky, if we were to say 1 was our answer, we'd be dismissing the denominators : x-1 = 0, we can't have 0 in the denominators!
Since both sides have a common denominator it is simple to rewrite the equation
x − 1 x = x − 1 1
by subtracting the right hand side from both sides to get
x − 1 x − x − 1 1 = x − 1 x − 1 = 0
The expression on the left hand side has the value 1 for all x except x = 1 where it is undefined.
There is no x that can satisfy this equation.
X^2 -2x +1 =0 , x=1 ..no solution.. Denominator is 0 ..
Since it's a multiple choice question, it would make sense to substitute all the possible options into the equation.
Clearly when x=1, division by zero occurs and x=0 does not satisfy the equation.
Hence the answer is no solution.
by inspection, multiply both sides of the equation by x-1, this will cancel out the denominators, what results is x=1. but any number divided by 0 is infinity therefore in the equation x/(x-1)=1/(x-1), infinity=infinity. this equation is absurd, no solution. ha..ha, just remembered the fallacious proof.
What about over C, the complex numbers?
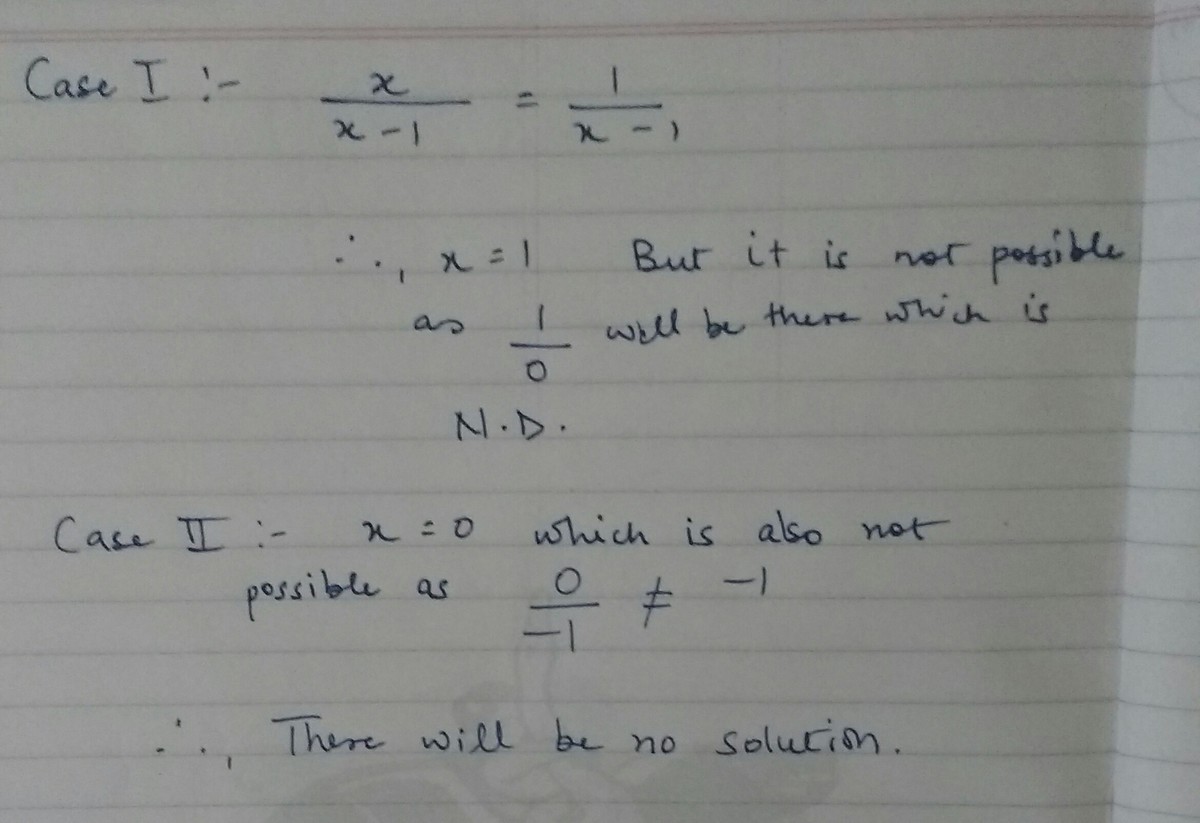
From the equation x − 1 x = x − 1 1
We get by cross multiplying that
x ( x − 1 ) = ( x − 1 )
⟹ x 2 − 2 x + 1 = 0
⟹ ( x − 1 ) 2 = 0
⟹ x = 1
Now putting x = 1 in the equation above, we get,
0 1 = 0 1
Now, this is not defined, hence x=1 is not a solution of the equation, Rather, it has 0 solutions as the only solution we got doesn't satisfy the equation.
Hence x has 0 solutions or NO SOLUTIONS