Just do it
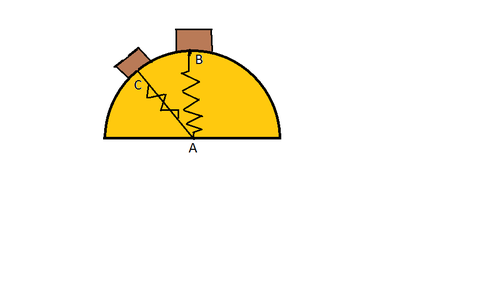 A 2 kg block is gently pushed from rest at B slides down the smooth circular surface shown in the figure. A spring of strength
N/m (attached at the origin of the hemisphere) pulls the block tight against the surface.
A 2 kg block is gently pushed from rest at B slides down the smooth circular surface shown in the figure. A spring of strength
N/m (attached at the origin of the hemisphere) pulls the block tight against the surface.
What is the unstretched length of the spring (in m) if the spring keeps the block in contact with the surface until the angle with the vertical is 60 degrees?
Assumptions and Details
- The radius of the hemisphere is 1.5 m
- is 60 degrees
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Suppose the extension in the spring is x .
Three forces are acting on the block--
(1) m g (2) Force due to extension in the spring = k x (3) Normal reaction form the hemisphere.
As the work done by last two forces are zero so we can use conservation of energy to find the velocity of the block at the required instant. Let that velocity be v .
So m g R ( 1 − c o s ( 6 0 ) ) = 0 . 5 m v 2 .....(1)
When it leaves contact with the hemisphere centripetal force would be provided by force due to spring and a component of m g .
So m v 2 / R = k x + m g c o s ( 6 0 ) .......(2)
Using 1) and 2) we get x = 0 . 5 So natural length of the spring is 1 c m .