Just hanging around- part 1
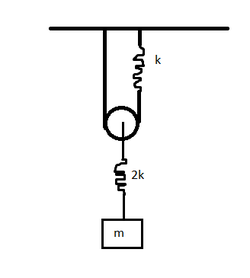 If the time period of simple harmonic motion of the rectangular block can be represented as
T
=
2
π
b
k
a
m
for coprime positive integers
a
,
b
.
If the time period of simple harmonic motion of the rectangular block can be represented as
T
=
2
π
b
k
a
m
for coprime positive integers
a
,
b
.
Find a 2 + b 2 up to two decimal places.
Details and Assumptions
- Pulley is smooth and massless, and the strings are light and inextensible.
- Gravity is present.
- The crooked lines in the figure represents springs of spring constant k and 2 k as shown.
-Take the amplitude of oscillations to be very small.
The answer is 5.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
How come the upper spring is extended by 2x if the pulley's diplacement is just x? I know your answer is right but why 2x?
Log in to reply
If you move the pulley down 1 cm, the string/spring system gets 2 cm longer, 1 cm on each side. We are told that the string is "inextensible", so, the spring is extended by 2 cm.
Log in to reply
Thanks a lot :)
Why won't the spring only extend in downward direction to a distance of 1 cm? As per your analysis center of mass of spring remains the same even if it is stretched from one end?
Let extension in the top spring be y 1 and the extension of the lower spring be y 2 .
Now, the tension is uniform throughout the string, and the tension T , pulls at both points of contact with the ceiling, thus for the balance of forces on the massless string, we have
T − k y 1 = 0
For the balance of forces on the massless pulley, we have
0 a = 2 T − 2 k y 2 = 2 k y 1 − 2 k y 2
which implies y 1 = y 2
The total displacement for the rectangular block is given by y = 2 y 1 + y 2 = 2 3 y 2
Now for the block, we have
m d t 2 d 2 y = m g − 2 k y 2 = m g − 3 4 k y
If we perform the change of variables, y → y e q + Δ y , where y e q = 4 k 3 m g , we have
m d t 2 d 2 y = − 3 4 k y
which is the usual equation for simple harmonic motion, and we find
ω = 3 m 4 k
a = 3 , b = 4
a 2 + b 2 =5
Not offensive .... But bro seriously Level-5 ?
Log in to reply
I m also surprised i wrote it is easy. Bhaiya pls check my report inyour previous question fearless because your reposted question also have a diff answer form than mine .My answer doent have "e". Pls mail me.
Log in to reply
No It is absolutly correct , check it once more ... I changed the phrasing .... Also feel free to call me by my name deepanshu :)
Also I did not see any report from you .... have you reported in Repost or in previous post .
well you know? i am really surprised that there is a rope under the spring with constant k at first i think it's a spring only.well if it's a rope i agree your answer is right
Hi Gautam,
In your first equation, for the balance of forces on the pulley, you have
0 = i ∑ F i = 2 k y 2 − 2 k y 1
as far as the balance of forces being equal to zero, I agree.
However, you state that y 1 is the extension of spring one, and y 2 is the extension of spring two. The force exerted by spring two should definitely be 2 k y 2 , as you say. However, if the extension in spring one is y 1 , then why is the force exerted by spring one on the pulley not simply k y 1 ?
There is a second way of looking at the problem. If the position of the pulley is extended by Δ y , then the force exerted by the first spring is 2 Δ y k . Thus, the first spring-string contraption has an effective spring constant 2 k .
Then, this setup is simply a series arrangement of two springs of strength 2 k , which add as parallel resistors do so that the effective spring constant of the spring in series is k eff = k . Then, the frequency of the mass m is simply k / m . This is the same result we obtain if the correction is made in your first equation.
Can you tell me why I'm wrong?
Log in to reply
Hi josh,
See the figure and maybe that will make it clear.
Let the tension in upper string be T .Hence on pulley 2T force will act upwards and So we know
T
=
k
y
1
.

Log in to reply
Mustn't T also support the weight m g ?
Log in to reply
@Josh Silverman – Yes ,it will but i had taken net displacement and also mg force just changes the equilibrium position the time period of SHM will remain same.It can be seen simply that let the initial extension in the springs be y 1 0 a n d y 2 0 then in equation this term will also come and as these were in equilibrium state initially hence the net force by these initial extensions would be equal to mg (and opposite)and hence mg term will vanish from eq. Hope this helps others too.
Log in to reply
@Gautam Sharma – Also It is already mentioned gravity is absent.
Log in to reply
@Satvik Choudhary – No it is written the gravity is present @satvik choudhary
hey if we see the two springs are in series therefore k equivalent= k therefore 2kl=mw^23/2l where l=expansion of the spring right ???
why is the displacement y1/2+y2?
This was a difficult question, you know. Should have been on level 4 at least.
What is the value of "delta y", I cant see it bro :(
It can also be done by writing mechanical energy equation and since no external force other than gravity acts therefore differentiate that equation and equate to 0.
Suppose we see the system when it is not in equilibrium. The two springs having displacements x(1) &x (2). The mass m applies force F=mw^2x on the spring which causes displacement x (1)= F/2k. Since the spring is masssless( gravity free condition) it pulls the pulley with the force F and ultimately force F/2 is transmitted to the 2nd spring x (2)=F/2k. The total dispacement is x (1)+x (2)/2 = 3F/4k. Finally F=mw^2 (3F/4k). w= 2♡(pi) (3m/4k)^1/2. a=3 b= 4.
Suppose we see the system when it is not in equilibrium. The two springs having displacements x(1) &x (2). The mass m applies force F=mw^2x on the spring which causes displacement x (1)= F/2k. Since the spring is masssless( gravity free condition) it pulls the pulley with the force F and ultimately force F/2 is transmitted to the 2nd spring x (2)=F/2k. The total dispacement is x (1)+x (2)/2 = 3F/4k. Finally F=mw^2 (3F/4k). w= 2♡(pi) (3m/4k)^1/2. a=3 b= 4.
Gravity doesn't make a difference in time period it only changes the equilibrium position.
Let x be the (downward) displacement of the pulley (from equilibrium). Then the upper spring is extended by 2 x , creating a tension of 2 k x in the rope. Since this tension acts on both sides of the pulley, we have an upward force of 4 k x on the pulley.
Now let y be the (downward) displacement of the block of mass m . Then the lower spring is extended by y − x , and it will exert a downward force of 2 k ( y − x ) on the pulley. Since the net force on the pulley must be zero, we have 4 k x = 2 k ( y − x ) , or, x = 3 y . Now the lower spring exerts an upward force of F = 2 k ( y − x ) = 3 4 k y on the block, meaning that the effective spring constant for the whole system is k e f f = y F = 3 4 k .
Finally the period is T = 2 π k e f f m = 2 π 4 k 3 m , with a = 3 and b = 4 .