Just like Gianlino's Disc. Only 1000 times easier
 Points
A
and
B
are placed at
(
2
,
0
)
and
(
−
2
,
0
)
respectively. A circle of radius 3 is then drawn centered at the origin.
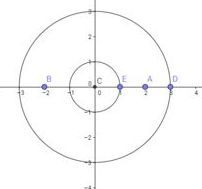
Points
A
and
B
are placed at
(
2
,
0
)
and
(
−
2
,
0
)
respectively. A circle of radius 3 is then drawn centered at the origin.
Next, a point E is randomly placed on the circumference of circle C centered at the origin with radius 1.
If the probability that the circumcenter of △ A B E lies within the circle of radius 3 can be represented by n m where m , n are coprime positive integers, find m+n.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions

Very unique. Never thought to do this. Great job!
Nice solution!
pls explain the last part...
Log in to reply
I have drawn one interval of the graph of y=|sin x|
Now for any value of x between 0 and pi, the required probability can be obtained by
(favoring values of x)/(sample space)=( (5pi/6-pi/6) /pi)
Note the I took an interval of pi as the graph's period is pi
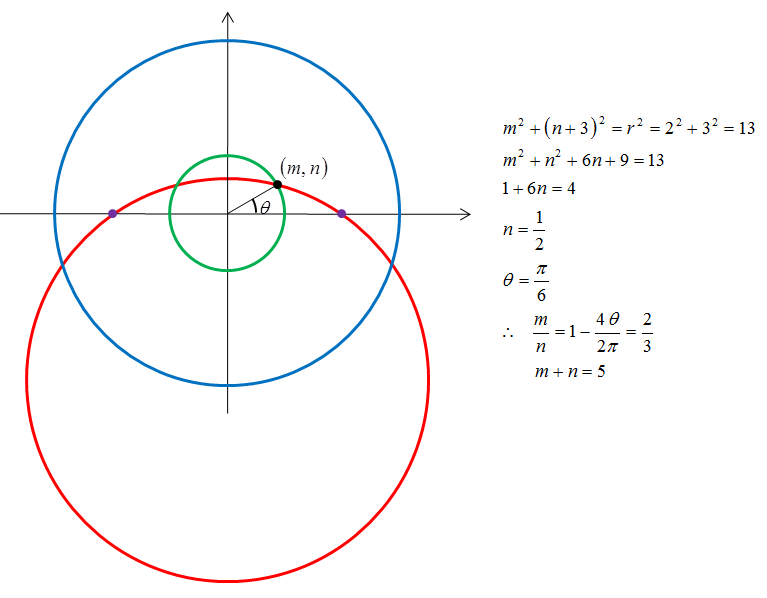
First thing to note, is that the circumcenter is situated on the y-axis, regardless of where point E is at. This is so because the circumcenter is a point which the perpendicular bisectors of A B , A E and E B will intersect, and the perpendicular bisector of A B would just be the line x = 0 .
Due to symmetry, we just have to focus on the first quadrant of the circle. Let O be the origin, and ∠ E O A = a . Now, when a is smaller than a certain value k ° , the circumcenter will be out of the circle of radius 3. When a is bigger however, but not more than 90°, the circumcenter will be within the circle. So what we need to do is find that value of k . To do that, we make the circumcenter situate at ( 0 , 3 )

From the fact that the (black) circle's center is ( 0 , 3 ) , and it passes through ( 2 , 0 ) , we can find, through Pythagoras theorem, the radius of the circle as 1 3 . Redrawing the diagram, we get

Through this, we can find the value of k using the cosine rule, which happens to be 3 0 .
Therefore, if 0 ° < ∠ E O A < 3 0 ° , the circumcenter would be out of the circle of radius 3 . If 9 0 ° > ∠ E O A > 3 0 ° , the circumcenter would be in the circle.
Hence, the probability that the circumcenter is in the circle or radius 3 is 9 0 9 0 − 3 0 = 3 2
But wait... then the answer should be 5 ...
This simulator might help.
Moderator note:
Nice approach of this problem.
The problem is supposed to say "outside". So yes, as it is, the answer should be 5.
Log in to reply
Thanks. I have updated the answer to 5.
Log in to reply
I think a more clear graphic should be put up in place of the original here. In general, how does one change the cover image? Once it's put in, it's out of reach.
Also, I notice that I had left this problem on because I got interrupted for some hours. When I got back and solved this, the "median time to solve" must have shot up to 175 minutes!
How does is this "median time to solve" computed? That is, how is anyone's time on a particular problem computed?
Log in to reply
@Michael Mendrin – I always have tabs on for days, it'll probably screw up the median.
@Michael Mendrin – I'm not sure, but the "time to solve" feature is very unusual.
Because outliers for the time would tend to be quite high and many in numbers, I feel that mean time should be used for harder problems that have fewer solvers because people may take days to solve a tougher problem.
LOL, I actually learned something this year in AP Stat relevant to life :3
Log in to reply
@Trevor Arashiro – I think "[average or median] time to solve" is going to be as easy as trying to nail jello on the wall. On one hand, I can see the value of having some kind of a metric like that, but on the other hand, what does that even mean? How is the "time it takes to solve" is even measured? If I glance at a problem on day, go away and maybe think about it, and when I realize that I've got the answer, and put it in, what's the total time it took me to solve it? Even I don't know, so it would be fascinating if Brilliant could tell me that.
Can you explain what you are doing here? Note that the n m in your solution has nothing to do with that stated in the question.
Log in to reply
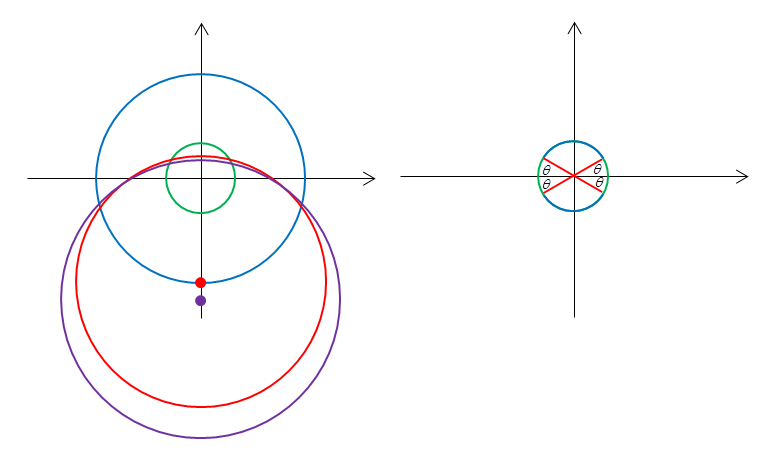
If 0 < θ < π/6, the circumcenter of △ABE will lie outside the circle of radius 3.
If E placed on the green colour part of the circumference of circle C centered at the origin with radius 1, the circumcenter of △ABE will lie outside the circle of radius 3.
Log in to reply
Well, my point is to avoid an abuse of notation by having m and n stand for 2 different things. m stands for both the x-coordinate of some point, and also the numerator of the probability. This makes it confusing for what you are tying to say.
It doesn't help that you only have equations written down, with no explanations whatsoever for what you are trying to accomplish.
Consider E As (cosx , sinx)
It is easy to observe that circumcentre lies on the line x=0
Now just write the equation of perpendicular bisector of one side in terms cosx and sinx and calculate y coordinate.
That will be -3/2 sinx
Just its modulus should be less than 3 to lie in interior of circle