Just look carefully!

Calculus Level 5

Let $f$ be a twice differentiable function defined on $x>0$ satisfying $x f(y) + y f(x) = f(xy)$ for all $x,y> 0$ . Given that $f'(1) = 1$ , find $\displaystyle 4\sum_{x=1}^\infty f''(x) f''(x+2)$ .

The answer is 3.

1 solution

Abhi Kumbale
May 21, 2016

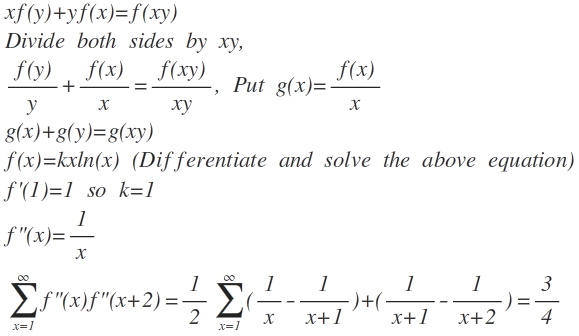
Fun problem!

My approach is similar to Abhi's:

Differentiating with respect to $y$ gives $xf'(y)+f(x)=xf'(xy)$ . Now evaluate at $y=1$ to find $x+f(x)=xf'(x)$ . Next differentiate with respect to $x$ to get $1+f'(x)=f'(x)+xf''(x)$ or $f''(x)=\frac{1}{x}$ . My "end game" is the same as Abhi's.

Otto Bretscher - 5 years ago

It would've been more fun if it was only given that f is continuous and we had to prove that f was infinitely differentiable! ;)

@Otto Bretscher

A Former Brilliant Member - 5 years ago

This is an exercise often assigned in calculus classes; essentially Cauchy's functional equation. It becomes (a lot) more interesting when you drop continuity.

Otto Bretscher - 5 years ago

@Otto Bretscher – Yeah. When you drop continuity, you get a function whose graph is dense on $\mathbb{R}^2$ right?

A Former Brilliant Member - 5 years ago

I have added two more problems which are "more fun". Check them out,

1.https://brilliant.org/problems/just-look-carefully-3/?ref_id=1202148

2.https://brilliant.org/problems/just-look-carefully-2-2/?ref_id=1202134

Try the first one first.

@Otto Bretscher, @Deeparaj Bhat

Abhi Kumbale - 5 years ago

@Abhi Kumbale – You can try these too,

https://brilliant.org/problems/convergency-and-divergency/?ref_id=1198750

https://brilliant.org/problems/generalization-of-a-problem-unique-symmetry/?ref_id=1198647

https://brilliant.org/problems/a-perfect-set-for-jee/?ref_id=1197855

They are all part of my set,

https://brilliant.org/profile/abhi-pwu19k/sets/my-creations-check-them-out/?ref_id=1198669

Abhi Kumbale - 5 years ago

Is this your own problem ? Great problem !! This is so much fun !

nishchith s - 4 years, 8 months ago

Just look carefully!

The answer is 3.

1 solution

0 pending reports