A number theory problem by Vitor Santos
x , y , z , t are all integers satisfying the following system of equations: { x z − 2 y t x t + y z = 3 = 1 . Find x 2 + y 2 + z 2 + t 2 .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
See Ivan's solution to understand how this problem is motivated by thinking about factorization in the Euclidean domain Z [ − 2 ] .
For a rigorous solution, be careful that you don't make the assumption of "the values have to be small". The equations do not yet directly yield a bound on the possible values of the variables.
@Mark Hennings Can you please explain why x & y are co-prime. Thanks
Log in to reply
Since x t + y z = 1 , any integer dividing both x and y divides 1 , so is ± 1 .
Why did you check if 11 divides e or not.
Apart from x and y , co-prime are z and t as well. Solving the system in x and y as a result yields x = z 2 + 2 t 2 3 z + 2 t and y = z 2 + 2 t 2 z − 3 t . For x and y to be integers, there has to be z − 3 t = k ( z 2 + 2 t 2 ) and 3 z + 2 t = l ( z 2 + 2 t 2 ) , for some k , l ∈ Z . Multiplying the first relation by 2 , and the second by 3 and summing both relation, there follows 1 1 z = ( z 2 + 2 t 2 ) ( 2 k + 3 l ) . Since z and t are co-prime, z and z 2 + 2 t 2 have no common divisors, we conclude z 2 + 2 t 2 must divide 1 1 , whence z = ± 1 and t = 0 or z = ± 3 , t = ± 1 , meaning x = 1 and y = 0 or x = 3 and y = 1 or x = − 3 and y = − 1 . So, x 2 + y 2 + z 2 + t 2 = 1 1 .
For solving { x z − 2 y t = 3 x t + y z = 1 I'll do some algebraic manipulations involving complex numbers.
- Let − 2 = ( i 2 ) 2 , substituting on the first equation will lead to x z + ( i 2 ) 2 y t = 3 .
- Multipling the second one by ( i 2 ) , leading to ( i 2 ) x t + ( i 2 ) y z = ( i 2 ) .
- Aligning the two equations x z + ( i 2 ) 2 y t = 3 ( i 2 ) x t + ( i 2 ) y z = i 2 and summing then up.
- Lefting us with x z + ( i 2 ) x t + ( i 2 ) 2 y t + ( i 2 ) y z = 3 + i 2 ⇒ x ( z + t 2 i ) + y 2 i ( z + t 2 i ) = 3 + 2 i ⇒ ( z + t 2 i ) ( x + y 2 i ) = 3 + 2 i .
- Applying moduli both sides wields ∣ ( z + t 2 i ) ( x + y 2 i ) ∣ = ∣ 3 + 2 i ∣ ⇒ ∣ ( z + t 2 i ) ∣ ⋅ ∣ ( x + y 2 i ) ∣ = ∣ 3 + 2 i ∣ .
- Using a complex number modulus, we have ( z 2 + 2 t 2 ) ⋅ ( x 2 + 2 y 2 ) = 1 1 ⇒ ( z 2 + 2 t 2 ) ⋅ ( x 2 + 2 y 2 ) = 1 1
- Now for using some number theory, if z , x , y , t ∈ Z then their squares belong to Z too. So we have, in the last equation, a product of two integers resulting in a integer. There is only one product of integers resulting in 1 1 which is 1 ⋅ 1 1 .
- z 2 + 2 t 2 = 1 ∧ x 2 + 2 y 2 = 1 1 , and the symmetry of the equations will lead to the same answers, no need of breaking this to two or more cases.
- Testing for small integers, e.g. 0 , 1 , 2 , equation z 2 + 2 t 2 = 1 leads to t = 0 , z = ± 1 and x 2 + 2 y 2 = 1 1 to x = ± 3 , y = ± 1 .
- Thus x 2 + y 2 + z 2 + t 2 ⇒ 9 + 1 + 1 + 0 = 1 1
Very nice interpretation!
The first half of the proof could be simplified to the identity:
1 1 = ( x z − 2 y t ) 2 + 2 ( x y + y z ) 2 = ( z 2 + 2 t 2 ) ( x 2 + 2 y 2 )
This is actually equivalent to what you're saying. You are using the language of Norm in Z [ 2 ] as the motivator, but I think it's clearer to just be explicit about the identity (since thinking in Z [ − 2 ] doesn't confer any additional benefits.
Log in to reply
I disagree. I think introducing the concept of Z [ i 2 ] is very fruitful! Writing u = x + y i 2 , v = z + t i 2 , the equations read u v = 3 + i 2 ,and so we are trying to factorise 3 + i 2 in the Euclidean domain Z [ i 2 ] . Since 3 + i 2 has prime norm, it is irreducible in Z [ i 2 ] , and hence one of u , v is a unit. The only units in Z [ i 2 ] are ± 1 , and we are done.
Looked at from this perspective, the question is more Algebra than Number Theory!
Log in to reply
Yes, that's the Z [ − 2 ] argument, which (I believe) is the motivation behind the problem.
My statement about "be explicit about the identity, and avoid talking about Z [ − 2 ] stems from the perspective of a problem solver who has not seen Z [ − 2 ] , and so would feel more resistance to understanding these proofs. Because the concepts used are very basic, and their proofs do not require understanding of Z [ − 2 ] , in such a case I think it's better to first present the proof and then second show the linkage to this other area of math.
Log in to reply
@Calvin Lin – Fair enough, but "where did that identity spring from?" and "how am I expected to have thought of it?" become legitimate responses if you just write the identity down!
We work in Z [ − 2 ] ; that is, numbers in the form a + b − 2 . If p = a + b − 2 ∈ Z [ − 2 ] , define ∣ p ∣ = a 2 + 2 b 2 ; this is the square of the usual norm in complex field. We can prove that ∣ p q ∣ = ∣ p ∣ ⋅ ∣ q ∣ , and if a , b are integers, then so as ∣ a + b − 2 ∣ .
Now, suppose we have x + y − 2 and z + t − 2 . Their product is ( x z − 2 y t ) + ( x t + y z ) − 2 , or 3 + − 2 . Thus we're trying to factorize this number.
Note that ∣ 3 + − 2 ∣ = 3 2 + 2 ⋅ 1 2 = 1 1 . If 3 + − 2 factors to x + y − 2 and z + − 2 , then 11 must also factor to ∣ x + y − 2 ∣ and ∣ z + t − 2 ∣ . Thus one of them is 11 and the other is 1. Without loss of generality, assume ∣ x + y − 2 ∣ = 1 1 and ∣ z + t − 2 ∣ = 1 .
Since ∣ z + t − 2 ∣ = z 2 + 2 t 2 , clearly we have t = 0 (any other integer t makes the sum larger than 1) and z 2 = 1 . With a little casework, we also find that x 2 = 9 , y 2 = 1 is the only integer solution to ∣ x + y − 2 ∣ = x 2 + 2 y 2 = 1 1 . Thus we have x 2 + y 2 + z 2 + t 2 = 9 + 1 + 1 + 0 = 1 1 . In other words, this means 3 + − 2 is irreducible, because if we try to factor it into a product of two numbers, one of the factors must be 1 or -1, so we don't simplify it at all. (Compare with 4 + − 2 = ( 1 + − 2 ) ( 2 − − 2 ) .)
See my note to Vitor's solution...
squaring both equations: { x 2 z 2 − 4 x y z t + 4 y 2 t 2 x 2 t 2 + 2 x y z t + y 2 z 2 = 9 = 1
sum up (Eq1)² and ( 2 × Eq2²): x 2 ( z 2 + 2 t 2 ) + y 2 ( 4 t 2 + 2 z 2 ) = 9 + 2 .
which can be factored as ( x 2 + 2 y 2 ) ( z 2 + 2 t 2 ) = 1 1
Then x 2 , y 2 , z 2 , t 2 are non negative integers, which yield a factorisation 1 1 = 1 ⋅ 1 1 or 1 1 = 1 1 ⋅ 1 . It is clear now that it suffices to check when x 2 , y 2 , z 2 , t 2 have values in { 0 2 , 1 2 , 2 2 , 3 2 } , thus the possible sums of form a 2 + 2 b 2 :
sum b 2 0 2 1 2 2 2 a 2 2 b 2 0 2 8 0 0 2 8 1 1 3 9 4 4 6 − 9 9 1 1 −
Therefore, { ( x , y ) , ( z , t ) } = { ( 0 , 1 ) , ( 1 , 3 ) } and thus x 2 + y 2 + z 2 + t 2 = 0 2 + 1 2 + 1 2 + 3 2 = 1 1 .
This is by far the easiest solution to follow; but there are two minor problems with the last line. The ordered pairs are reversed, and negative values for x,y,z, and t are acceptable.
{(x,y),(z,t)} = {(±1,0),(±3,±1)}
Going back to the original equations, the three non-zero x,y,z,t must be all positive or all negative.
Just play around till you come up with the idea to put t = 0 . Then it is easy but has many solutions. The smallest solution for which all are integers is x = 3 , y = z = 1 which gives answer 11.
How do you know that t cannot be (say) 100?
You will get (x^2-2y^2)(2t^2-z^2) = -7, since all the variables are integers, it would be easy to find solutions.
i did same wow
Good solution
What makes you say that "Deom >= Num"? Are you assuming that t is positive?
More accurately, what we want to do is to consider cases where |Deom| > |Num|, and proceed from there. Unfortunately, I think this gets tricky to rule out in the 2 variable case (but I might be wrong).
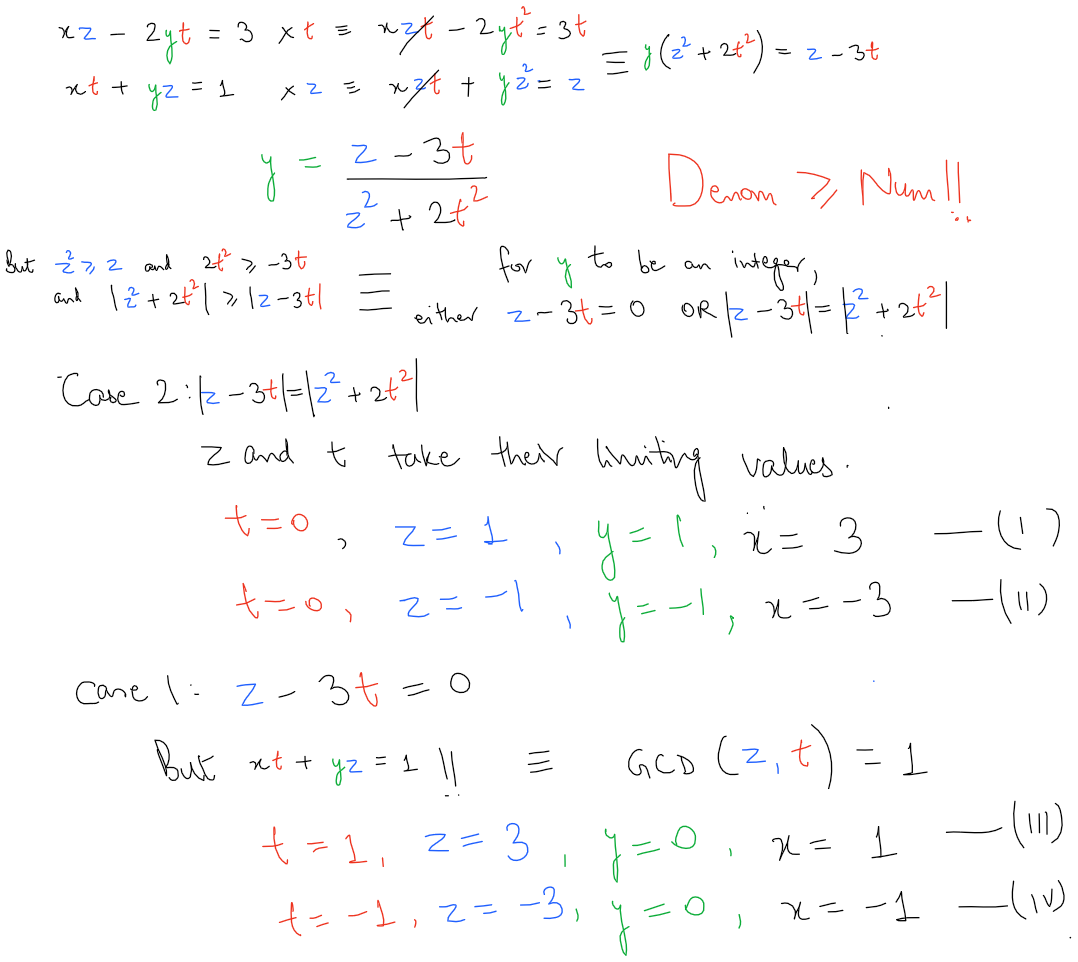
SInce x t + y z = 1 , x and y are coprime. Now x z − 2 y t = 3 ( x t + y z ) , so we see that x ( z − 3 t ) = y ( 3 z + 2 t ) and hence, since x and y are coprime, we have 3 z + 2 t = e x z − 3 t = e y for some integer e . Since x t + y z = 1 we deduce that e = z 2 + 2 t 2 There are two cases to consider:
If 1 1 divides e , we have e = 1 1 f for some integer, and hence z = f ( 3 x + 2 y ) , t = f ( x − 3 y ) , and 1 = x t + y z = f ( x 2 + 2 y 2 ) . This means that f = 1 , x = ± 1 and y = 0 , and hence z = 3 x and t = x
If e and 1 1 are coprime then, since e divides both 3 z + 2 t and z − 3 t , it follows that e divides both 1 1 z and 1 1 t , so we deduce that e divides both z and t . But that means that e divides 1 = x t + y z . Since e = z 2 + 2 t 2 ≥ 0 , we deduce that e = 1 , and hence x = 3 z + 2 t y = z − 3 t z 2 + 2 t 2 = 1 Thus we deduce that t = 0 and z = ± 1 , so that x = 3 z and y = z .
Thus there are just four solutions in integers to these equations, namely ( x , y , z , t ) = ( 1 , 0 , 3 , 1 ) , ( − 1 , 0 , − 3 , − 1 ) , ( 3 , 1 , 1 , 0 ) , ( − 3 , − 1 , − 1 , 0 ) . In all four cases we have x 2 + y 2 + z 2 + t 2 = 1 1 .