Kinematics With Portals
If you have never played the video game Portal, a portal is essentially a wormhole (or tunnel) which can teleport an object from one location to another instantaneously, almost as if the object had simply passed through a door. The portal will conserve kinetic energy and speed. However, the object's direction of travel will get shifted depending on how the portals are oriented relative to each other. In math-speak, the object's velocity vector relative to the first portal is equal to that same object's velocity vector relative to the second portal.
Now for the problem:
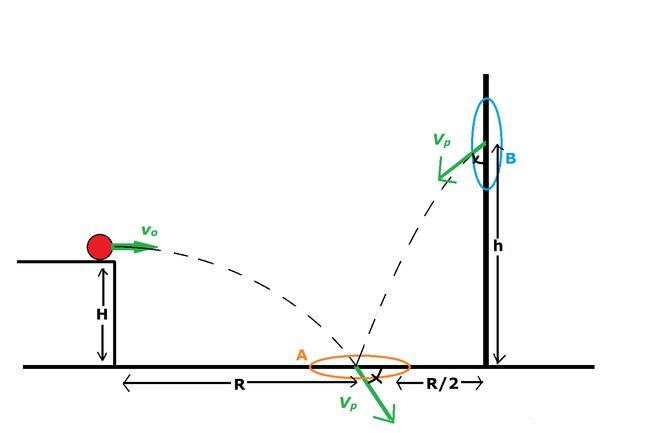
A ball is launched horizontally off of a ledge of height at an initial speed of . Portal A (orange) is placed on the ground at a distance such that the ball will pass directly through the portal's center.
On a wall a distance away, Portal B (blue) is placed at a height such that, after the ball passes through, it will again fall into Portal A , but from the other side.
Note that the angle at which the ball falls into Portal A (relative to the ground) is the same as the angle at which the ball falls out of Portal B (relative to the wall).
Given that and , find .
Give your answer in meters, rounded to 3 significant figures.
Take the acceleration due to gravity as .
The answer is 0.408.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let t 0 A be the time it takes for the ball to fall from its starting position to portal A, and let t B A be the time it takes for the ball to fall from portal B to portal A.
Also, let v A x and v A y be the x- and y- components of the ball's velocity just as it enters portal A. Let v B x and v B y be the x- and y- components of the ball's velocity just as it leaves portal B.
Note that because portal B is perpendicular to portal A, the x- and y- coordinates of the ball's velocity will simply "trade places." That is,
v B x = v A y and v B y = v A x
First, we solve the kinematics equations describing the ball's trajectory from its starting point to portal A for R and v A y . Note that v A x = v 0 .
R = v 0 t 0 A
H = 2 1 g t 0 A 2 => t 0 A = g 2 H
=> R = v 0 g 2 H
v A y = g t 0 A = 2 g H
After the ball goes through the portal, the x- and y- coordinates "trade places," so:
v B x = 2 g H and v B y = v 0
Again, we use kinematics, but this time the ball's horizontal displacement is 2 R and its vertical displacement is h , so
2 R = v B x t B A
Substituting in our formulas for R and v B x , this becomes
2 v 0 g 2 H = t B A 2 g H => t B A = 2 g v 0
We also know that:
h = v B y t B A + 2 1 g t B A 2
Performing the appropriate substitutions, this becomes:
h = 2 g v 0 2 + 2 g 4 g 2 v 0 2
which simplifies to:
h = 8 g 5 v 0 2
Finally, plug in the numbes:
h = 8 ( 9 . 8 1 s 2 m ) 5 ( 2 . 5 3 s m ) 2 = h = 0 . 4 0 8 m