Kissing Circles! (Valentines Day)
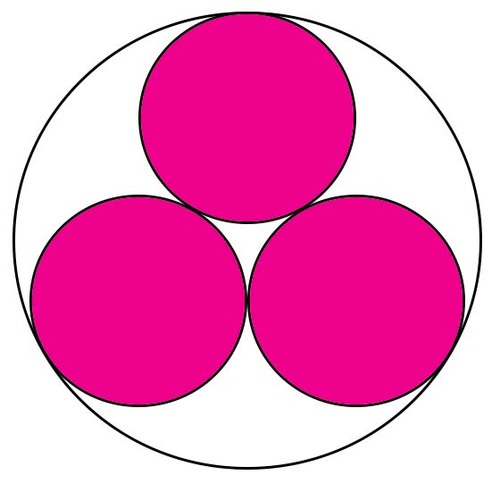 All of these circles are in LOVE! See how they kiss? Well, the larger circle wants to buy the smaller pink circles dresses but doesn't know their radii. Given that the radius of the larger circle is 1, what are the radii of the smaller pink circles? (All of the circles are externally or internally tangent to their neighbors)
All of these circles are in LOVE! See how they kiss? Well, the larger circle wants to buy the smaller pink circles dresses but doesn't know their radii. Given that the radius of the larger circle is 1, what are the radii of the smaller pink circles? (All of the circles are externally or internally tangent to their neighbors)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
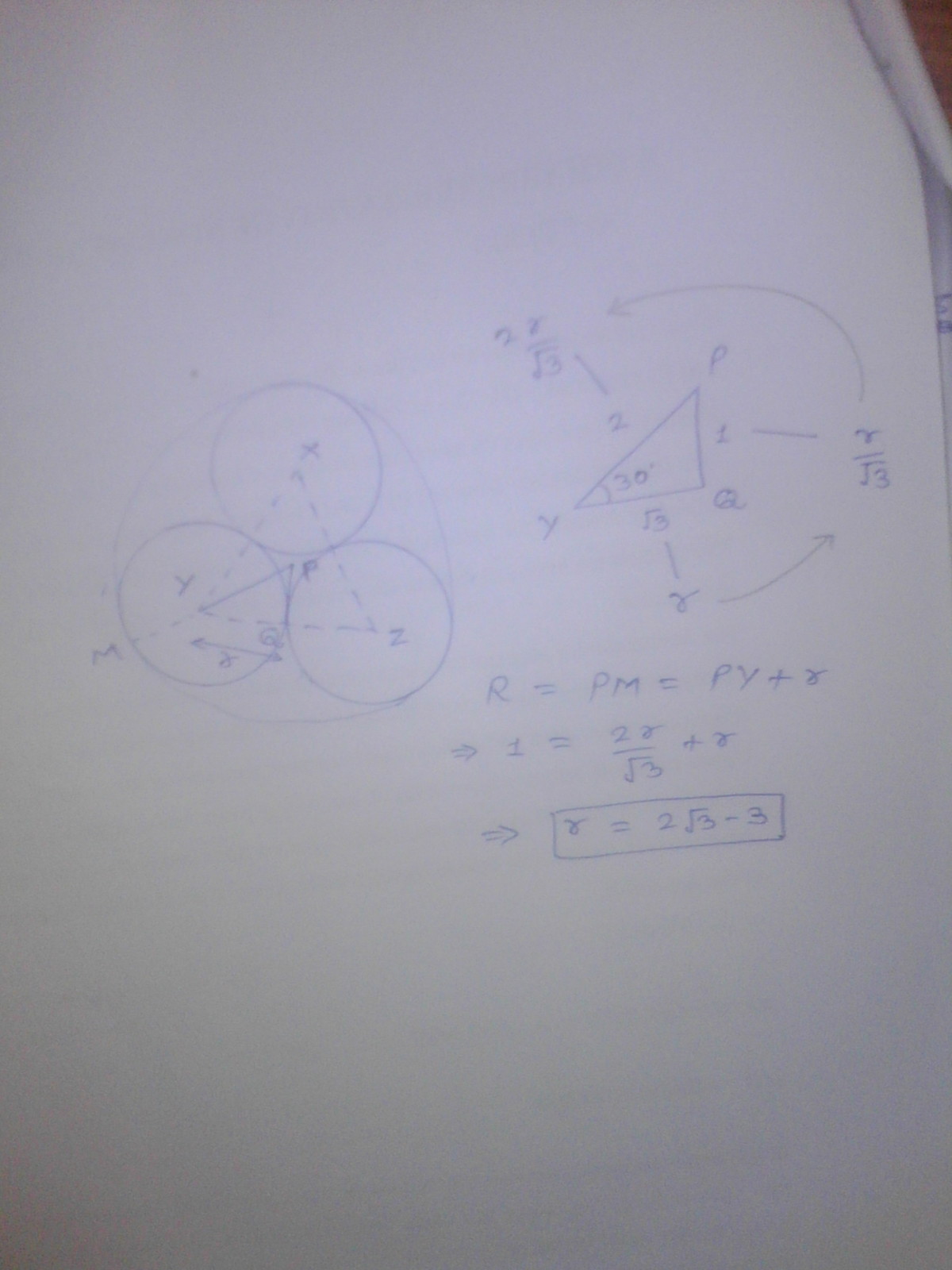
Let O be the center of the bigger circle
Let r be the radius of one of the small circles
Let A, B and C be the centers of the three small circles
In triangle OAB
OA = OB = 1 - r
AB = 2 r
angle AOB = 120
Applying cosine law in triangle OAB
(AB)^2 = (OA)^2 + (OB)^2 - 2(OA)(OB) cos 120
4 r^2 = 2(1 - r)^2 - 2(1 - r)^2 (-1/2)
4 r^2 = 3(1 - r)^2
2 r = (square root of 3)(1 - r)
Then
r = 2 (square root of 3) - 3
3 2 r + r = 1
r = 2 3 − 3
THE SIMPLEST SOLUTION (ONLY WORKING BECAUSE OF THE OPTIONS)
Since the radius of the larger circle is 1 the options C and D will not work as they will give a value greater than 1 . If we join the diameter of any 1 of the smaller circles and the center, we would see that the line will not be divided into a ratio of 1 : 1 : 1 by the center of the smaller circle and the point at the circumference which touches this line. Thus option A also won't satisfy. Hence we are only left with one option, that is, B
Kissing circles!!! That's quite a good interpretation William .
I see that you haven't entered your question into the Valentine's Day Themed Content Contest .
Do it quickly else you won't get enough votes, and Best of Luck !!
There's a contest for this? Well, I post it right away then! Thanks for the heads up!
Log in to reply
Great job on the submission . But you must remove the space between ]and( , you see, it should be like this. ](
Log in to reply
That took me a bit too long to figure out...
Log in to reply
@William Z – Oh, sorry for giving a vague answer .
Log in to reply
@A Former Brilliant Member – No, it not that, I didn't see your comment until after I fixed it.
Log in to reply
@William Z – Oh, I see ⌣ ¨
Log in to reply
@A Former Brilliant Member – BEST PROBLEM EVER.
Log in to reply
@Baby Googa – I suppose you are referring to this question , right ? It's quite easy though .
Log in to reply
@A Former Brilliant Member – Yes I was, whoever came up with it is a genius!
Log in to reply
@Baby Googa – Well I see that you have solved a lot of my problems , did you like them too ?
Log in to reply
@A Former Brilliant Member – Yes. I find them some of them very challenging.
This sum consists of mixed trigonometry, equations & geometric assumptions. Enjoyed a lot solving it.
This solution is a bit funky. I got the idea for this problem after seeing Descartes Theorem for Kissing Circles (I wish I made that up but, Rene beat me to it). So here is the wiki: Click here
Using Curvatures: The Curvature of the larger external circle is − 1 and the curvatures of the smaller congruent externally tangent circles will all be denoted by x .
Plugging into truncated equation:
k 4 = k 1 + k 2 + k 3 ± 2 k 1 k 2 + k 2 k 3 + k 3 k 1
We get
− 1 = x + x + x ± 2 x 2 + x 2 + x 2
Simplifying the equation to solve for x we get
− 1 = 3 x ± 2 3 x 2 ⟹ − 1 = 3 x ± 2 x 3 ⟹ − 1 = x ( 3 ± 2 3 ) ⟹ 3 ± 2 3 − 1 = x
Just to clean it up a bit, I’ll multiply the top and bottom by − 1 to get
x = − 3 ± 2 3 1
Finally, since x is the curvature, otherwise known as the reciprocal of the radius, we flip the fraction. We reject the negative case because we can’t have a negative radius and get the answer to be x = − 3 + 2 3 .
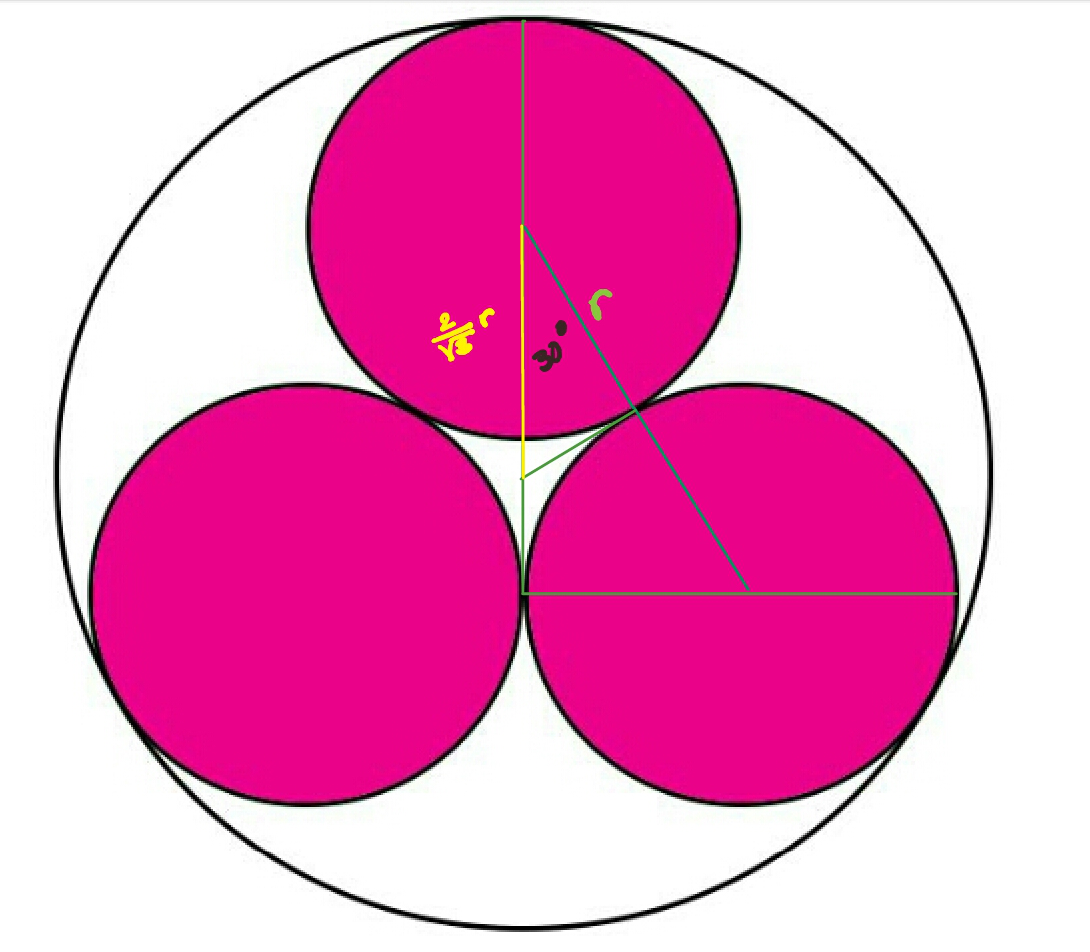
Join the centers of the three pink, radius r circles. This will form an equilateral triangle with side lengths 2 r . The incenter of this triangle coincides with the center of the larger circle.
Now draw a radius from the center of the larger circle through the center of one of the pink circles to the point where these two circles are tangent. Since the distance from the incenter of an equilateral triangle to one of its vertices is 3 2 the length of an altitude of the triangle, this radius will have length
3 2 ∗ 2 r sin ( 6 0 ∘ ) + r = 1 ⟹ r ( 3 2 + 1 ) = 1 ⟹ r = 2 + 3 3 = 2 3 − 3 .