Knights
Logic
Level
2
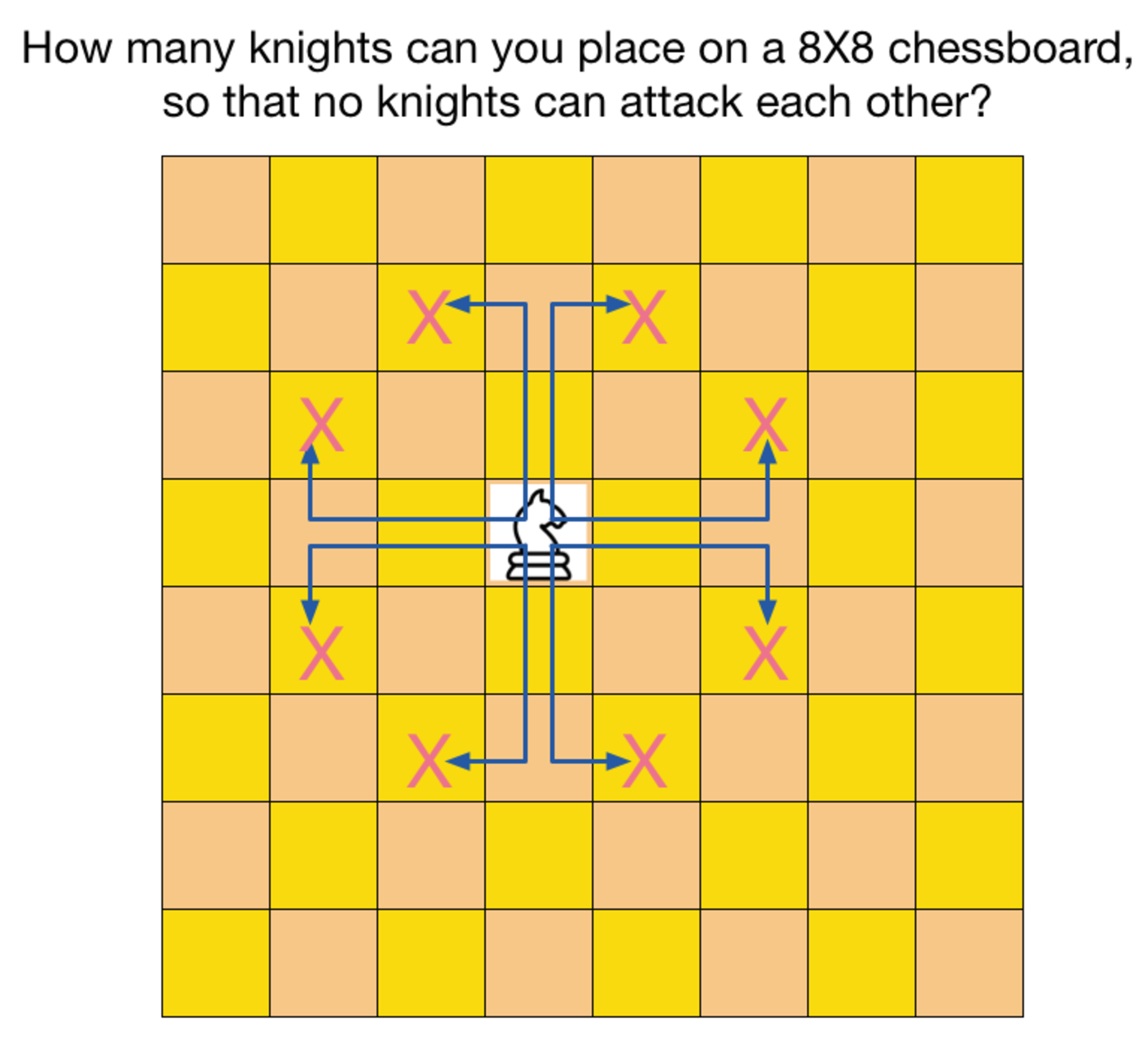
What is the maximum number of knights in an chessboard, so that no knights can attack each other?
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
1) First, we show that 32 is possible.
Place the knights on the 32 white squares. Then, the squares that such a knight attacks must be black, hence it doesn't attack any other knight that is on a white square.
2) Now, we show that 32 is an upper bound.
Break up the board into 8 smaller boards of size 2 × 4 . In each board, label the squares as such:
On each of these smaller boards, we see that we can place at most 1 knight in each of the pairs of squares with the same number, since these pairs of squares attack each other. Hence, there are at most 4 knights on this small board.
Since we have 8 different small boards, this shows us that we can have at most 8 × 4 = 3 2 knights on the total chessboard.