Know the functioning of the function?
Let f ( x ) be a polynomial. It is known that for all x ,
f ( x ) f ( 2 x 2 ) = f ( 2 x 3 + x )
If f ( 0 ) = 1 and f ( 2 ) + f ( 3 ) = 1 2 5 , find f ( 5 ) .
The answer is 676.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Note that f ( x ) ≡ 0 is not a solution, because it is given that f ( 0 ) = 1 .
Yes u r right!! So what's the approach without assuming it a polynomial?
Log in to reply
The times that i've seen this problem (or similar versions of it), I believe that it states the assumption of a polynomial (of finite degree)
In terms of finding functions that satisfy the functional equation, we could do stuff with algebraic closure of 2 , and define the function at those values to be ( 1 + x 2 ) 2 , while the function everywhere else is 0.
Of course, this doesn't get around that the question is asking for f ( 5 ) . So, maybe there is another way to only solve this for Q ( 2 ) , without resorting to polynomial arguments? (not sure)
Can you please explain this in a more shorter and simpler way? Because I get confused at some places, like the step where you used the 'triangle' inequality and then wrote alpha n+1 in terms of alpha n..
Your proof has several shortcomings.
First, having ∣ 2 α 2 + 1 ∣ = 1 and ∣ α ∣ = 1 effectively implies that α 2 = − 1 but you did not prove it.
Second, you proved that the only possible roots of f are i and − i but you did not prove that they have the same multiplicity and I don't even know whether it's true (currently I'm still working at it).
Log in to reply
- The first shortcoming was dealt with in showing 1 = ∣ 2 α 2 + 1 ∣ ≥ ∣ 2 α 2 ∣ − 1 = 1 which implies (skipping a minor step) α 2 = − 1 .
- The second shortcoming is a valid criticism. We can demonstrate that multiplicity needs to be the same via setting f ( x ) = ( x − i ) a ( x + i ) b and evaluating when f ( x ) f ( 2 x 2 ) = f ( 2 x 3 + x ) . After verifying that ( x 2 + 1 ) ( ( 2 x 2 ) 2 + 1 ) = ( ( 2 x 3 + x ) 2 + 1 ) , we can divide out by ( x 2 + 1 ) and so we only need to check when f ( x ) = ( x − i ) or f ( x ) = ( x + i ) , neither of which hold.
Log in to reply
Alright for the second shortcoming, I was about to post my solution involving a Taylor expansion (in order to avoid massive coefficients) to the first order when injecting f ( x ) = ( x − i ) a ( x + i ) b in f ( x ) f ( 2 x 2 ) = f ( 2 x 3 + x ) , yielding a − b = 0 .
About the first shortcoming, I wasn't criticising the premises but rather the implication, which isn't that minor to me. You need to remind that ∣ α ∣ = 1 and then split up the square of ∣ 2 α 2 + 1 ∣ using complex conjugation, to show that R e ( α 2 ) = − 1 and finally use ∣ α 2 ∣ 2 = 1 to get I m ( α 2 ) = 0 , yielding effectively α 2 = − 1 . Please let me know if you use a shorter way to calculate the intersection of two circles in the complex plane.
Log in to reply
@Maxence Seymat – For the first shortcoming, thinking about it as the intersection of 2 circles in the complex plane is indeed one way to approach it (and that's the gut reaction that I had since this brute force approach of setting α = a + b i is guaranteed to work).
Do you understand what I wrote up above? Ravi used a different method that happened to work in this case. From (a modified version of) the triangle inequality, we get that
1 = ∣ 2 α 2 + 1 ∣ ≥ ∣ 2 α 2 ∣ − ∣ 1 ∣ = 2 ∣ α ∣ 2 − 1 = 1
Hence, equality must hold throughout, hence α 2 is in the opposite direction from 1, which means that α 2 = − 1 . (That's the minor step that I referenced).
Log in to reply
@Calvin Lin – I get it now, it's the equality case of the second triangle inequality. But this wasn't obvious to spot at all.
Let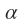 be a root of f(x).
be a root of f(x).
Then by given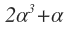 is also a zero of f.
is also a zero of f.
Triangle inequality implies that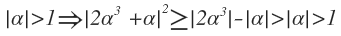
This gives infinitely many zeros by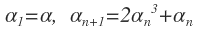 which is a contradiction.
which is a contradiction.
Comparing coefficinets of both sides of original given equation, we conclude that both the leading coefficient and f(0) are 1. f(0)=1=product of all zeros (by vieta's rule) in view of above contradiction and the fact that product of roots is 1, we get that all roots have absolute value=1. So
Then also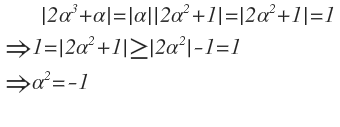
We conclude that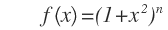
From f(2)+f(3)=125 we get n=2
So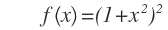
This yields f(5)=676