KVPY 2016 SA Question 16

Update : The concern raised with this comment has been dealt with.

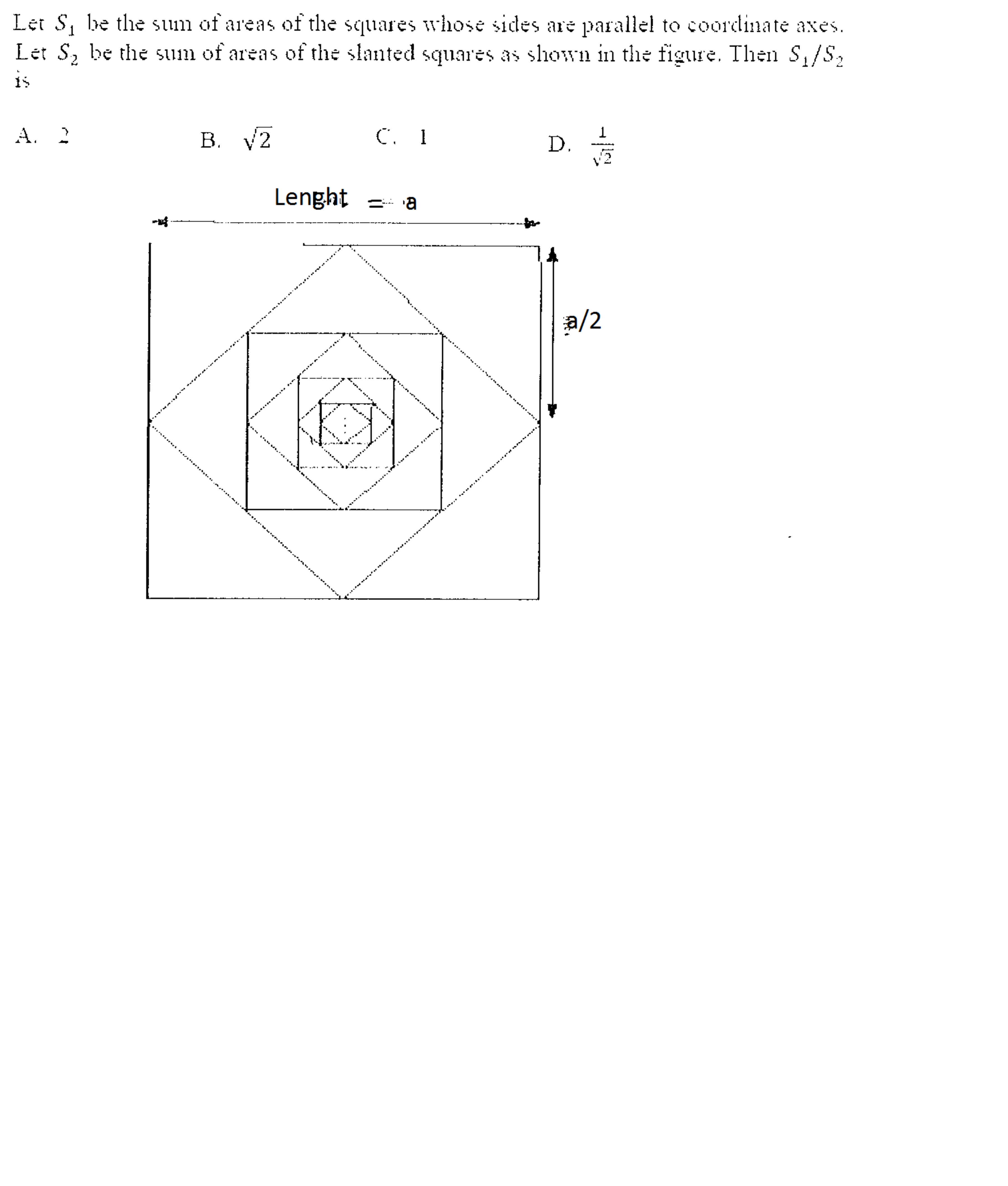
I don't think the question ever mentioned that the squares go till infinity. There are only 4 squares each (parallel and slanted) in the figure given.

However, your answer is luckily correct as the number of both types of squares were same in this problem.

The correct solution to this problem would be:

---

By geometry, we see that the sides of the parallel and slanted squares are in GP with common ratio $\dfrac 12$ . Also, the side length of the biggest parallel square is $a$ while that of the biggest slanted square is $\dfrac{a}{\sqrt 2}$ . Thus for $n$ squares each of the two types, we have

$\dfrac{A_1}{A_2} = \dfrac{a^2 \left( 1 + \frac 14 + \frac{1}{16} + \cdots \text{ n terms} \right)}{a^2 \left( \frac 12 + \frac 18 + \frac{1}{32} + \cdots \text{ n terms} \right)} = 2 \text{ for every positive integer n}$

$n=4$ or $n=\infty$ (sum of infinite GP) is just a trivial case here so as long as the number of both types are equal. (Yes, I know that infinity is not a number. Maybe my argument of comparison is wrong. But I just wanted to make you clear that the problem never mentioned about an infinite number of squares.)

In gp the infinite one and the finite one's ratio is preserved as it is multiple privative....so not completely a matter of luck as the number of squares is the same

Sorry its "multiplicative"

That's right absolutely

There are three dots at the centre....which ensure infinity