KVPY 2016 SA Question 6
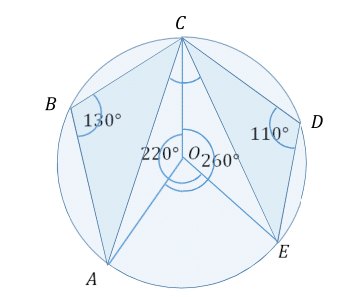
The points A , B , C , D , and E are marked on the circumference of a circle in order such that ∠ A B C = 1 3 0 ∘ and ∠ C D E = 1 1 0 ∘ .
Find the measure of the green angle, ∠ A C E , in degrees.
Note: The diagram is not necessarily up to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
I have another solution but I don't have premium so I'm going to post it here. We can clearly see that the triangle AEC has angles and lengths that are independent of the points B and D. Otherwise this problem wouldn't have a solution. From this we can gather that as long as B is between A and C, and D is between C and E, the angles ABC and CDE are 130 and 180, respectively. It doesn't matter how long any of the sides are besides AE, as long as they're all on the circumference. So there's no reason for ABC and CDE not to be isosceles triangles. I can't upload photos but this is pretty easy to imagine. Draw lines connecting C, B, and D all to the center of the circle. It's a circle so all the lines are the same length. So, if we put B equidistant from A and C, then the angle OBC is 65 (O being the origin, 65 being half of 130). This also makes OCB 65. Since B is equidistant from A and C, the intersection of the lines AC and OB is squared, meaning BCA = 90 - OBC. We know OCB is 65, and BCA is 25, so OCA is 40. Doing all the same steps on the D side, we get ODC = OCD = 55, DCE = 35, and so OCE = 20. ACE = OCA + OCE = 20 + 40 = 60. Hopefully a member will read this and make a nice picture solution. It seems like a lot of steps but it's really simple. I didn't know what a cyclic quadrilateral or what inscribed angles were (as I'm sure many don't) so this is how I solved it. Thanks for reading if you read this. I hope the rest of your day is cool beans.
What information in the initial problem indicates a cyclic quadrilateral?
Log in to reply
They are inscribed in a circle, aren't they?
Log in to reply
Ah, I see what cyclic quadrilateral means now. I wasn't aware this theorem existed and had to use the theorems involving inscribed angles and central angles.
I was thrown by the poor drawing...60 was my original answer using the above logic, but changed it because the 50 deg angle looked bigger than the 60!
Log in to reply
Good point! I've added the line of "diagram isn't necessarily up to scale" to the question~
How do you know the 70 and the 50
Log in to reply
As Dhanvanth as shown, ABCE is cyclic quadrilateral, so angle ABC + angle AEC = 180. From this we get angle AEC = 50. Similar method can be applied to find angle CAE using quadrilateral AEDC.
my approach - angle ACE = angle ADE, as they're in the same segment. Using cyclic quadrilateral BCDA, angle CDA = 50, leaving ADE = 60
 The given angles
A
B
C
=
1
3
0
∘
and
C
D
E
=
1
1
0
∘
are
inscribed angles
.
The given angles
A
B
C
=
1
3
0
∘
and
C
D
E
=
1
1
0
∘
are
inscribed angles
.
The corresponding central angles are double the size. So we have 2 2 0 ∘ going around O on the left side from C to E , and 2 6 0 ∘ going around O on the right side from A to C .
They add up to 4 8 0 ∘ . This is once around plus the overlap, which is an angle A O E . So the measure of it is ∠ A O E = 4 8 0 ∘ − 3 6 0 ∘ = 1 2 0 ∘ .
This is a central angle. The corresponding inscribed angle is A C E = 2 1 2 0 = 6 0 ∘ .
I find your solution hard to follow because it's not immediately obvious what you meant by "external angles" and "internal angles".
I think the terms you're looking for are "acute angle", "obtuse angle" and "reflex angle". Is my interpretation correct?
Log in to reply
Sorry about the terminology. I hope I fixed the problem. Central and inscribed angles is what I meant.
Log in to reply
I finally understood your solution, but overall, it's still uneasy to read through, because it is not immediately obvious how you obtained the numbers you gave in the second paragraph.
If I were you, I would have explained how 220 came about by stating that
Since ACDE is a cyclic quadrilateral, then angle CAE = 180- 110 = 70, then obtuse angle COE = 2 * angle CAE = 140, and so the reflect angle of COE is just 360 - 140 = 220.
(Same goes for 260).
Overall, this looks good. Thanks for the dialog.
Log in to reply
@Pi Han Goh – Actually that was not how I got the figures. Maybe this makes is more clear.
@Pi Han Goh – @Pi Han Goh The below theorem has been used to deduce the angles at the centre. ( I don't know how to draw diagrams here, else would have provided the diagram too)
Angle at the Centre: The angle formed at the centre of the circle by lines originating from two points on the circle's circumference is double the angle formed on the circumference of the circle by lines originating from the same points.
Log in to reply
@Suman Roy – Ah, that clears things up. Thanks!
You can upload an image when you post a solution. Maybe you should post a solution too?
Thanks for this. Just : The AOC and EOC angle values are switched !
Log in to reply
Not quite. Take note of the reflex angle that is marked in the diagram. The angle AOC is going to be twice of angle ABC, but the central angle would refer to the reflex angle instead of the usual "internal" one that we would expect. So the 260 refers to reflex angle AOC, instead of the internal angle AOE.
That also tripped me up the first time I looked at the picture. Blindly using our default interpretation can trick us :)
The drawing has the 260 and 220 reversed
Log in to reply
Actually, the drawing does not have the angles reversed. The inscribed angle 1 1 0 ∘ on the right corresponds to the arc from C to E on the left and the central angle going from C to E , also on the left. And likewise for the angle of 1 3 0 ∘ which had its arc, and central angle, of double size on the right.
Too much of angle chasings there in all the solutions. Just join B E . Then ∠ C B E = 7 0 ∘ . => ∠ A B E = ∠ A C E = 1 3 0 ∘ − 7 0 ∘ = 4 0 ∘ .
Log in to reply
Nice and clean. Adding a line makes all the difference.
Marta, I like your solution better. Thanks.
Join AD. Now we can easily observe that ABCD is a cyclic quadrilateral. Therefore, angle ABC and angle CDA add up to 180 degree. Therefore angle CDA becomes 180-130=50 degree. Now angle ADE becomes 110-50=60 degree. Join AE. We can observe that AE chord subtends angle at point C of the circle. It also subtends angle at point D. Also we know that angles in same segment are equal, so angle ACE=angle ADE =60 degree
Yup, this is correct! Just like the other solutions~~
Although an image would your solution much more illuminating...
Your solution could be clearer if you stated the property of the cyclic quads that allows you to construct the first equation :)
Log in to reply
I don't bother about that ....everyone s giving the same solution ..what makes this one distinct from them is the visual representation.
Log in to reply
what software or application did you use to draw the figures?
Log in to reply
@A Former Brilliant Member – Microsoft paint sir
This is the only solution which clarify the problem for me.
Another elegant solution.
this is best solution ..still with least upvotes
- In a cyclic quadrilateral, the sum of the opposite angles is always equal to 1 8 0 ∘ .
- In a triangle, the sum of the angles in always equal to 1 8 0 ∘ .
Cyclic Quadrilateral:
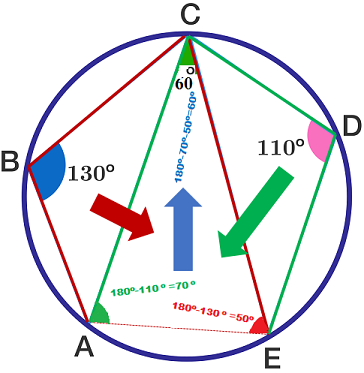
∠ A B C + ∠ A E C = 1 8 0 ∘ , Therefore ∠ A E C = 1 8 0 ∘ - ∠ A B C = 1 8 0 ∘ - 1 3 0 ∘ = 5 0 ∘ .
∠ C D E + ∠ C A E = 1 8 0 ∘ , Therefore ∠ C A E = 1 8 0 ∘ - ∠ C D E = 1 8 0 ∘ - 1 1 0 ∘ = 7 0 ∘ .
Triangle:
∠ C A E + ∠ A E C + ∠ E C A = 1 8 0 ∘ , Therefore ∠ E C A = 1 8 0 ∘ - ∠ C A E - ∠ A E C = 1 8 0 ∘ - 7 0 ∘ - 5 0 ∘ = 6 0 ∘ .
Each step is clear and justified by the facts you provided, and this is what makes it a great solution :)
This is a simpler solution
Since,m(CEA) arc = 2x130=260
M(EBC)=2x110=220
Hence, Arc AE is common for the previously mentioned arcs
, Since m(AC)=220-AE
M(EC)=260-AE
Then Using acummulative angles identity for circle
260-AE+(220-AE) + AE = 360
...
480-2AE+AE=480-AE=360
Then m arc AE = 120
Since green angle is inscribed of arc AE then measure green angle = 60
Could you please explain what the function m here is?
You can see that ABCE & ACDE are cyclic quadrilaterals . So the sum of the opposite angles of a cyclic quadrilateral is always 1 8 0 ∘ .
Using this, angle CAE and CEA are 7 0 ∘ and 5 0 ∘
The sum of the angles of a triangle must be 1 8 0 ∘ .So angle ACE is 6 0 ∘