L-Tetramino

Geometry Level 3

You are sitting and staring at the ground and notice the square tiles placed in a $9 × 5$ matrix.

So you wonder whether you can fill them up with L-Tetraminos (picture of them below)

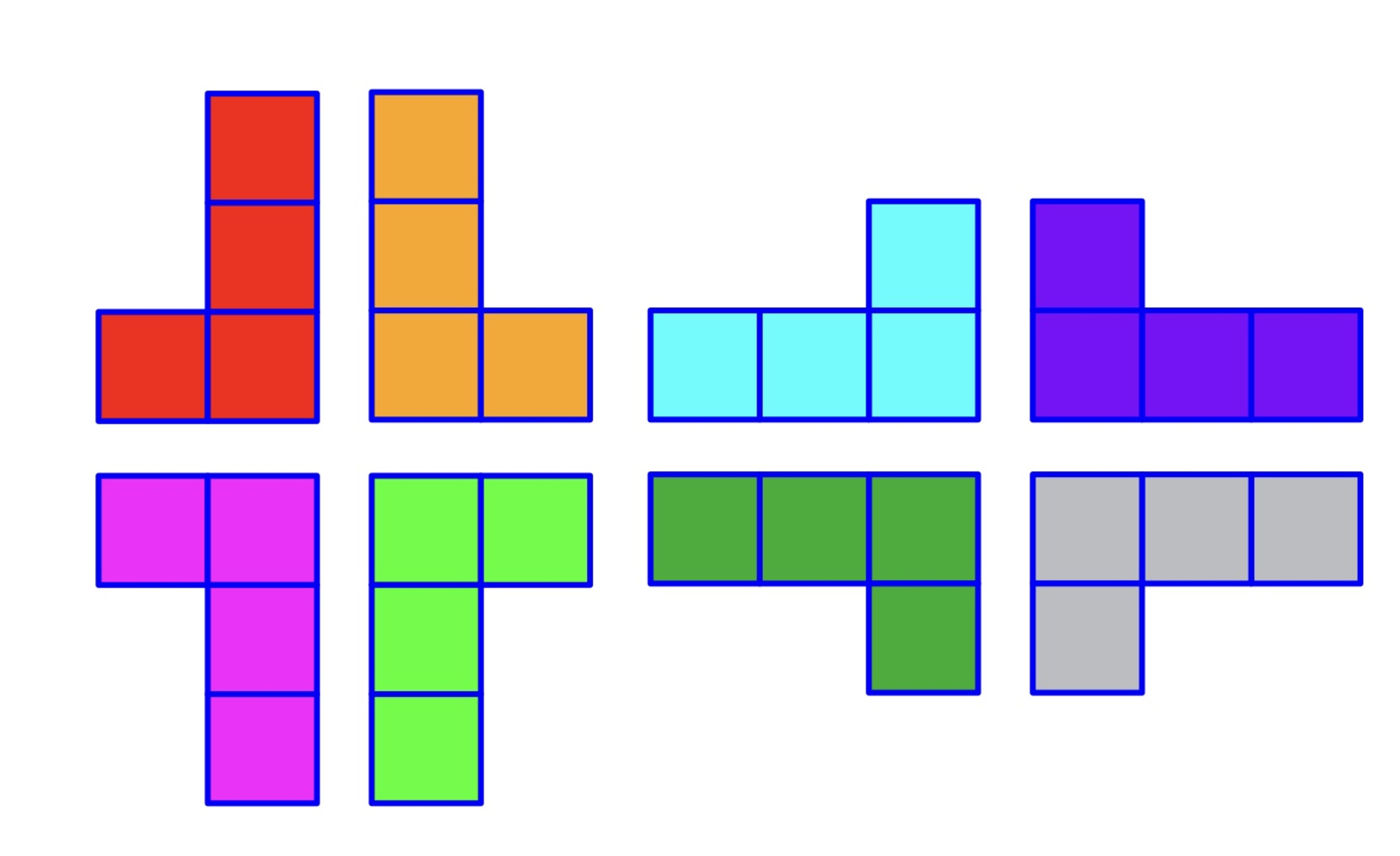
You know after filling in as much as possible there will be one hole left, so you wonder where you can place that hole.

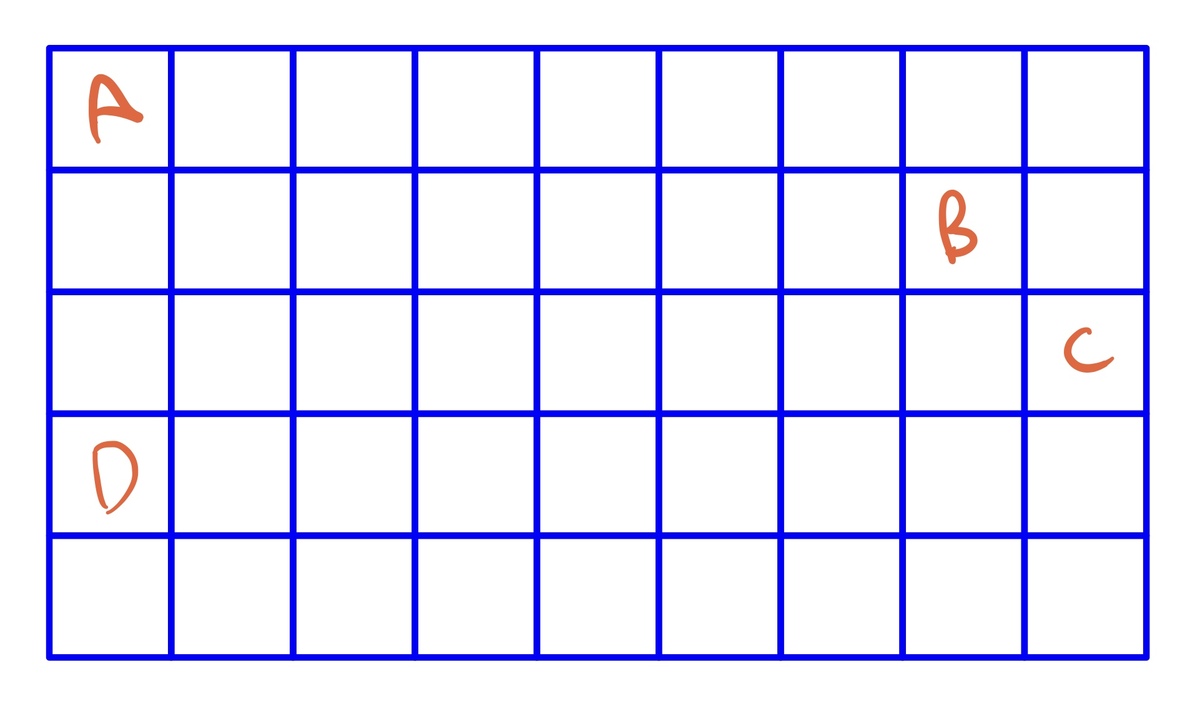
Out of the given options, in only one place can the hole be placed, which is it $?$

$\textbf{Example : }$ Of a $5 × 5$ matrix filled with one corner empty

A B C D

1 solution

David Vreken
Feb 23, 2021

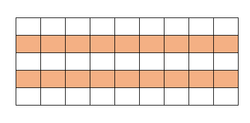
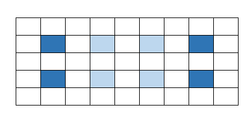
Color every other column white and gray so that there are $20$ gray squares and $25$ white squares:

Then there are two types of L-Tetraminos that can be placed on the board - one that covers $1$ white square and $3$ gray squares, and one that covers $3$ white squares and $1$ gray square:

Let $x$ be the number of L-Tetraminos that cover $1$ white square and $3$ gray squares, and let $y$ be the number of L-Tetraminos that cover $3$ white squares and $1$ gray square.

Since each L-Tetramino covers $4$ squares, and since there are $45$ squares and $1$ hole, there are $\cfrac{45 - 1}{4} = 11$ total L-Tetraminos, so $x + y = 11$ .

Assume that the hole is on a white square, so that all $20$ gray squares are covered. Then $3x + y = 20$ . However, $x + y = 11$ and $3x + y = 20$ leads to $(x, y) = \bigg(\cfrac{9}{2}, \cfrac{13}{2}\bigg)$ , a non-integer solution, which is not possible. Therefore, the hole must be on a gray square.

Out of the given choices, only B is on a gray square, so that is where the hole should be placed.

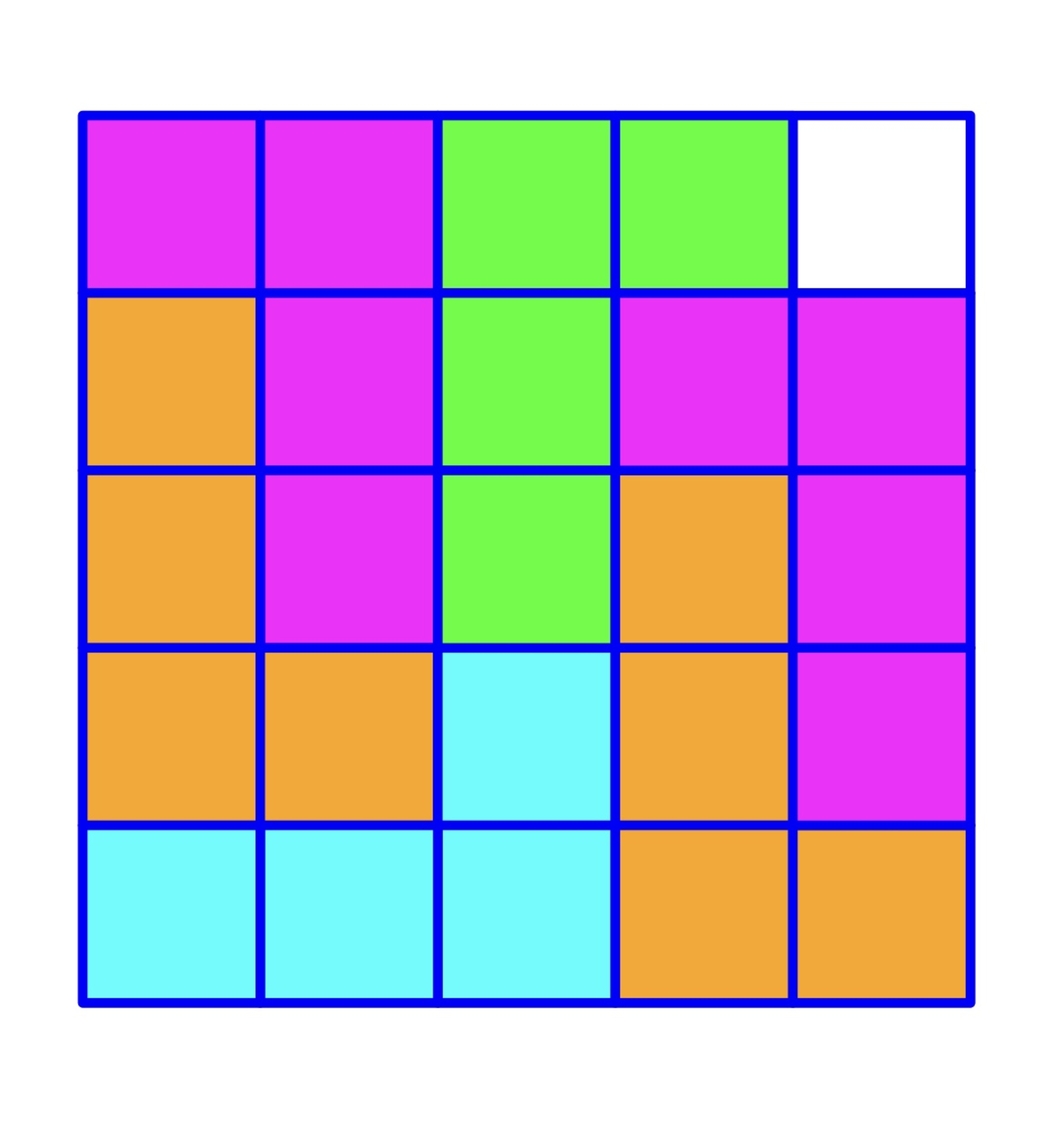
Here is one possible way to do this:

I knew it, it had to be colouring, why did this never cross my mind for years, thank you @David Vreken

Jason Gomez - 3 months, 2 weeks ago

Great solution (and a fun problem).

Interestingly, if you apply the same idea with horizontal stripes it works as well (although not for this problem, as it doesn't separate cases B and D). Following the same logic, the hole has to be one of the orange cells below:

and combining with David's solution, the hole can only be one of the blue shaded cells:

By symmetry, the dark blue cells are equivalent to cell B in the original diagram. The light blue cells do indeed also work.

So that's $9\times 5$ ...I wonder what we can say about $m \times n$ grids based on this?

Chris Lewis - 3 months, 2 weeks ago

This is how my bathroom tiles on the wall are arranged and from six I have been unable to solve this, through exhaustive case analysis(in otherwords trying everything possible) I found out that that were the only places where the hole went, never could get the proof, then I learnt colouring, still didn’t get any proof, was reminded recently about this and still realised I had no proof lol

Jason Gomez - 3 months, 2 weeks ago

That is a cool story. I remember stuff like that too - like thinking about the angles between the hands of an analogue clock, or when the display of a digital one would be symmetric. Maybe there's a market for indirect STEM inspiration products.

(actuallty, since you're here, @David Vreken - any similar recollections? I wonder how many people who get into this kind of maths share something like that in common)

Chris Lewis - 3 months, 2 weeks ago

@Chris Lewis – I've always had a fixation on trying to make a number sentence with the current time or date. (For example, today is 2/24/2021, and 2 + 2 - 4 = 2 + 0 - 2 * 1.) But I've also always liked brain-teasers and puzzles.

David Vreken - 3 months, 2 weeks ago

@Chris Lewis – Oh this reminds of the problem I had with car plates, I used to think if I line up 10000 cars then all numbers from 0001 to 9999 should be shown, but if I pick up a certain number like 0007 it might not be present, I was very confused for a very long time(mostly because I was dealing with “big numbers”).

Jason Gomez - 3 months, 2 weeks ago

You can also get the blue shaded cells by combining the vertical line pattern with a checkerboard pattern (or the horizontal line pattern with a checkerboard pattern). That's how I started out the solution but edited when I realized I only needed the vertical line pattern for this particular problem.

David Vreken - 3 months, 2 weeks ago

Wait how does checkerboard work, don’t all the orientations give two of the two different colors

Jason Gomez - 3 months, 2 weeks ago

@Jason Gomez – That's also how I started (and ruled out D) - you're right that each L covers two cells of each colour; but the whole grid has an odd number of cells...

Chris Lewis - 3 months, 2 weeks ago

@Chris Lewis – Oh like that

Jason Gomez - 3 months, 2 weeks ago

@Jason Gomez – If the grid is colored with a checkerboard pattern (and the top left square is shaded), then there are 22 white squares and 23 shaded squares. But each L-tetramino would cover 2 shaded and 2 white squares, so after tiling it as best as we can there will be 1 shaded square leftover. Therefore, the hole would have to be placed on one of the shaded squares in a checkerboard pattern.

David Vreken - 3 months, 2 weeks ago

@David Vreken – Now I feel even more foolish lol, I only did this colouring and then thought I should be doing colouring with three colours and got no where, should have analysed two colours back again or atleast the checkerboard

Jason Gomez - 3 months, 2 weeks ago

L-Tetramino

1 solution

0 pending reports