Ladder on the Stairs
A ladder is placed on a stairway (as shown). What is the length of the shorter leg?
Details and Assumptions
:
- Each step has the same horizontal run of 1 5 cm and vertical run of 1 0 cm .
- Each leg of the ladder rests on the horizontal midpoint of a step.
- The angles that the legs make with the steps are congruent.
The answer is 119.573.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Can you tell me how do you draw the diagram?
Log in to reply
Adobe Fireworks CS4:)
Log in to reply
Thank you!
Log in to reply
@Ong Zi Qian – For free software I quite like Figma just for your information
Log in to reply
@Dan Ley – Oh, I see! I am very weak on computer.
For the taller right triangle that you created, I'm confused as to how you know that its hypotenuse is 150 + d? You skipped over that step?
Log in to reply
It's true because I have chosen to extend it a length d beyond 1 5 0 . If instead your question is how a right triangle is formed, then that is due to the original triangle being isosceles. I left this as an intuitive step for the reader.
Is this problem supposed to be solved numerically? Is there a solution without it?
You could solve it (quartic equation) but it's tedious.
Continuing the lines per attached sketch, we can notice there is perfect symmetry to vertical axis CI (virtual symmetrical stairs and symmetrical line DE to AB drawn). Line AB (slope: 30 vertical, 45 horizontal, that is 10 vert,15 horiz) passes thru mid risers and mid treads of steps (risers 10cm, treads 15 cm). Both A and B are in the middle of a tread. Using the symmetry, we see that both AB and vertical axis CI pass thru mid tread of second step. Horizontal distance AI is exactly 2 treads = 30cm, base AD of isosceles triangle ACD is 60 cm. So:
h
2
+
3
0
2
=
1
5
0
2
( right triangle ACI or DCI)
h
2
=
2
1
,
6
0
0
h
=
1
4
6
.
9
7
( keeping 2 decimals)
also
cos
a
=
1
5
0
1
4
6
.
9
7
=
0
.
9
7
9
8
x
=
h
−
3
0
=
1
1
6
.
9
7
B
C
=
c
o
s
a
x
=
0
.
9
7
9
8
1
1
6
.
9
7
=
1
1
9
.
3
8
2
(keeping 3 decimals)

Hosam, it's a great question, but I put in 120, which is the fool's answer, and because of brilliant's rounding thing, it said it was correct. I'd suggest either specifying decimals in the answer, or modifying the question so the answer hit e.g. 119, which would be fun. Thanks for the question.
This logic is incorrect from the start. The location of the center depends on the ladder height. Imagine a ladder that has a very short right arm, say 12.5 cm. The left arm of length 62.5 will be just slightly above the steps and the center of the ladder will be above the edge of the right-most step. Although your answer is close to the correct one, it is coincidental only because of your initial drawing.
Log in to reply
I agree, the author of the problem clarified the formulation of the problem after my solution which is now only coincidental.
Ok, I see. The wrong assumption was the assumption that point E is located at the midpoint of the dashed step.
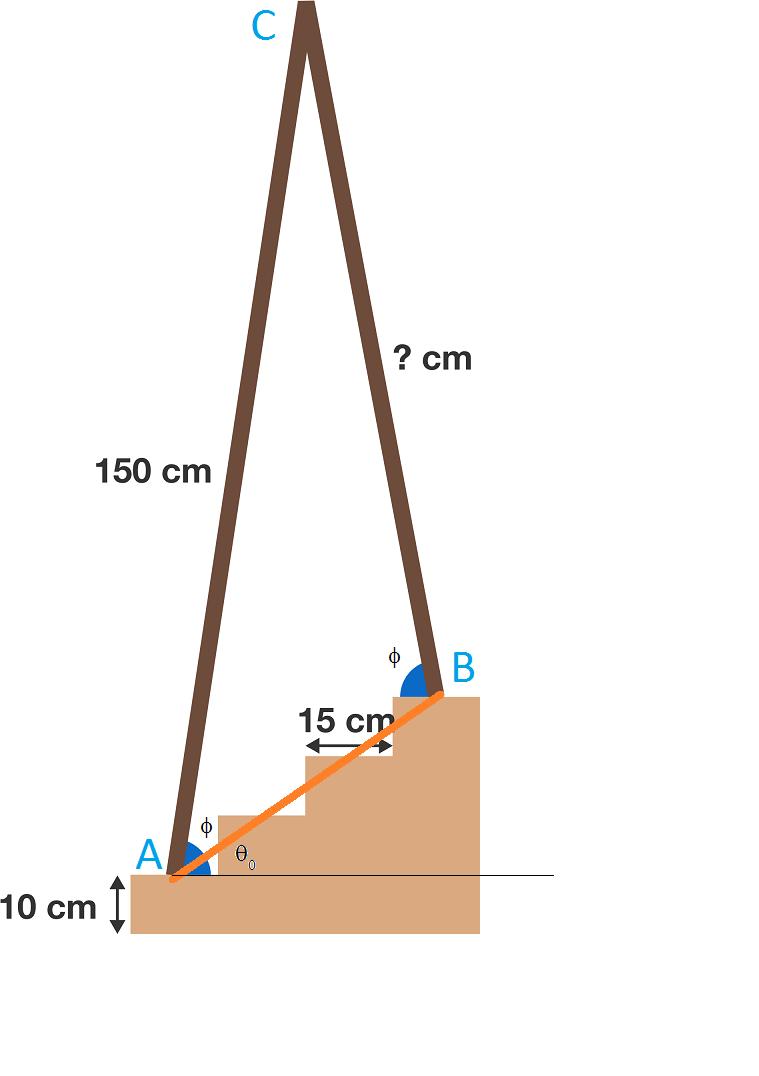 In my solution, I have used a trigonometric approach.
In my solution, I have used a trigonometric approach.
I have labelled the three vertices of interest as A, B and C, as shown in the above diagram. I have also connected the side AB.
Let ϕ be the angle that AC makes with the horizontal. Note that because of the imposed condition, ϕ is also the angle that BC makes with the horizontal.
With this, and taking A to be at the origin, it follows that the coordinates of C and B are given by
C = ( 1 5 0 cos ϕ , 1 5 0 sin ϕ ) ,
B = ( 4 5 , 3 0 )
The condition on the legs of the ladder implies that the slope of AC is the negative of the slope of BC.
Slope of A C = t a n ϕ = cos ϕ sin ϕ
Slope of B C = ( 1 5 0 cos ϕ − 4 5 ) ( 1 5 0 sin ϕ − 3 0 )
Therefore,
− cos ϕ sin ϕ = ( 1 5 0 cos ϕ − 4 5 ) ( 1 5 0 sin ϕ − 3 0 )
Cross multiplying, we obtain,
sin ϕ ( 4 5 − 1 5 0 cos ϕ ) = cos ϕ ( 1 5 0 sin ϕ − 3 0 )
Expanding and re-arranging,
3 0 0 sin ϕ cos ϕ − 3 0 cos ϕ − 4 5 sin ϕ = 0
Using the double angle sine formula, the above becomes,
1 5 0 sin 2 ϕ − 3 0 cos ϕ − 4 5 sin ϕ = 0
This equation can be solved using Newton's method for finding function roots. It goes as follows
Let f ( ϕ ) = 1 5 0 sin 2 ϕ − 3 0 cos ϕ − 4 5 sin ϕ be the function we want to find the root of.
First calculate the derivative, f ′ ( ϕ ) = 3 0 0 cos 2 ϕ + 3 0 sin ϕ − 4 5 cos ϕ
Secondly start with an initial guess ϕ 0 , and calculate successive approximations of the root using the following formula (Newton's Iteration)
ϕ n + 1 = ϕ n − f ′ ( ϕ n ) f ( ϕ n )
I started with ϕ 0 = 3 π
The method converged in 5 iterations to ϕ = 1 . 4 0 3 0 8 0 5 4 2 rad.
Now the length of BC can be calculated from the distance formula , as:
B C = ( 1 5 0 cos ϕ − 4 5 ) 2 + ( 1 5 0 sin ϕ − 3 0 ) 2 = 1 1 9 . 5 7 3
Should the solution be so complex..... the elementary method is more elegant i think.
Log in to reply
we all think that ... the symmetry method is especially elegant
Log in to reply
Whats the symmetry method ? Does it involve solving an equation numerically or an exact method?
Whats the elementary method ? Does it involve solving an equation numerically or an exact method?
This approach is uselessly complex for this problem that can be solved with just few mathematical passages.

Let assign h , a and θ as in the figure. Then h = 1 5 0 cos θ and a = 1 5 0 sin θ . We note that
tan θ cos θ sin θ 1 5 0 sin θ cos θ − 3 0 sin θ 3 0 0 sin θ cos θ − 3 0 sin θ − 4 5 cos θ 2 0 sin θ cos θ − 2 sin θ − 3 cos θ = h a = h − 3 0 4 5 − a = 1 5 0 cos θ − 3 0 4 5 − 1 5 0 sin θ = 4 5 cos θ − 1 5 0 sin θ cos θ = 0 = 0
Solving the equation numerically, we get θ ≈ 0 . 1 6 7 7 1 5 8 rad . Then, we have
x = ⎩ ⎪ ⎨ ⎪ ⎧ sin θ 4 5 − a = sin θ 4 5 − 1 5 0 sin θ cos θ h − 3 0 = cos θ 1 5 0 cos θ − 3 0 ≈ 1 1 9 . 5 7 3
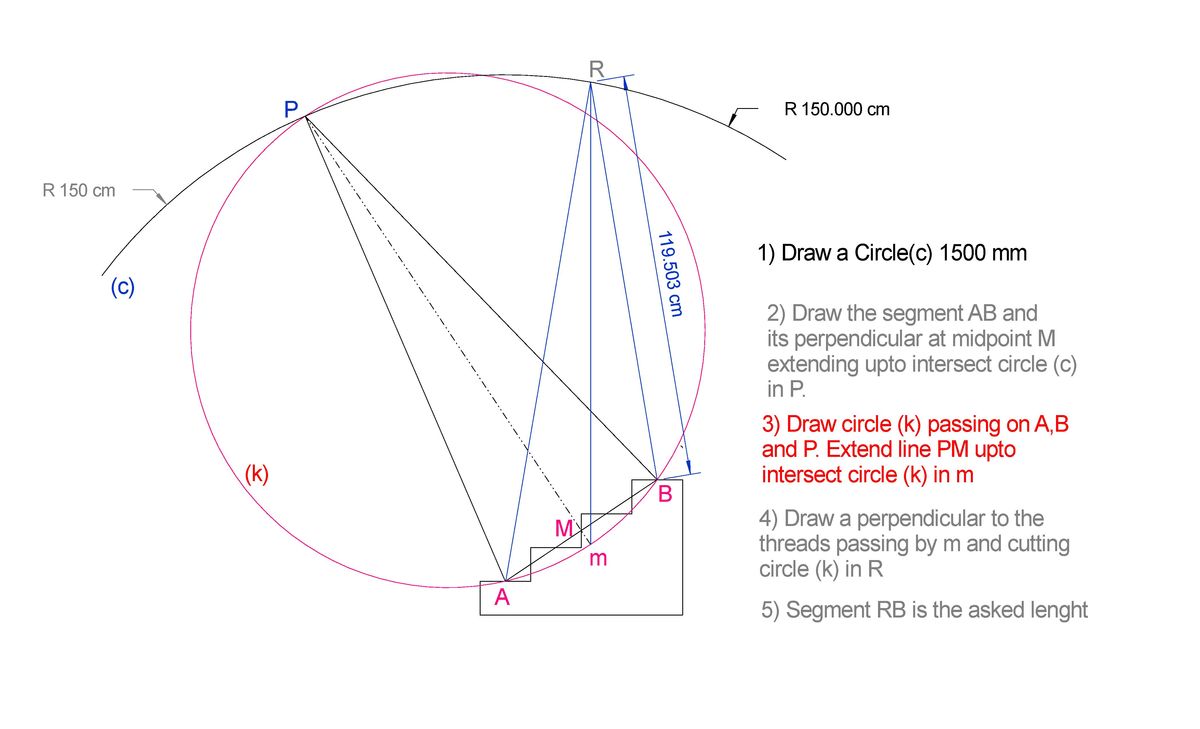
The angles of the ladder arms will not be equal with this construction. They will be equal only if point R lies on the red circle line. If R goes up or down, the angles become different. (put it as low as the upper step, for example)
Log in to reply
You are correct, but the point is that vertical line mR is the bisector of both angles at the top, since the triangles are isosceles. I intentionally erase the right lines joining the points A and B with the intersection of vertical at m with circle (k) not cramp the drawing..line were so close. But I forgot to make the oportune correction in step 4, it should say circle (c) instead of (k)
Log in to reply
It's true for any point at circle (k), but false for point R.
Log in to reply
@Andrey Zharkikh – Andrey, the angle at R obviously is not same than angle at P, however vertical line Rm does bisect angle ARB, since this vertical line will coincide as bisector of AIB, calling I the intersection point of the red circle with line mR not shown. Therefore if distance AR equal 150 the other leg must be 119.5
Using the law of cosines, one can compute the angles at the bottom of the triangle, $150^2 = 150^2 + 45^2 - 2 \cdot 150 \cdot 45 \cdot cos(A)$. A = 81.37 deg. Finally one can calculate the length of the size in question using the following equation (definition of sine) $sin(81.37)=\frac{30}{150-k}$. k=119.573
Make a right triangle out of the longer leg by creating a vertical line down from the apex of the ladder. We can calculate the height of that line this way:
150^2 = 22.5^2 + h^2
h= 148.3
Now we can create a right triangle with the shorter leg in the same fashion and the height of that will be 148.3 - 30 = 118.3.
So the two legs of a right triangle formed with the short leg as the hypotenuse are 22.5 and 118.3. So now the square root of (22.5^2 + 118.3^2) is the length of the short leg = 120.4 cm.
You must be a carpenter, this is the only solution I understand:-)
Your calculation of h is not correct. You assumed that the horizontal side if the triangle is 3*15/2 Instead it is approx 25.040
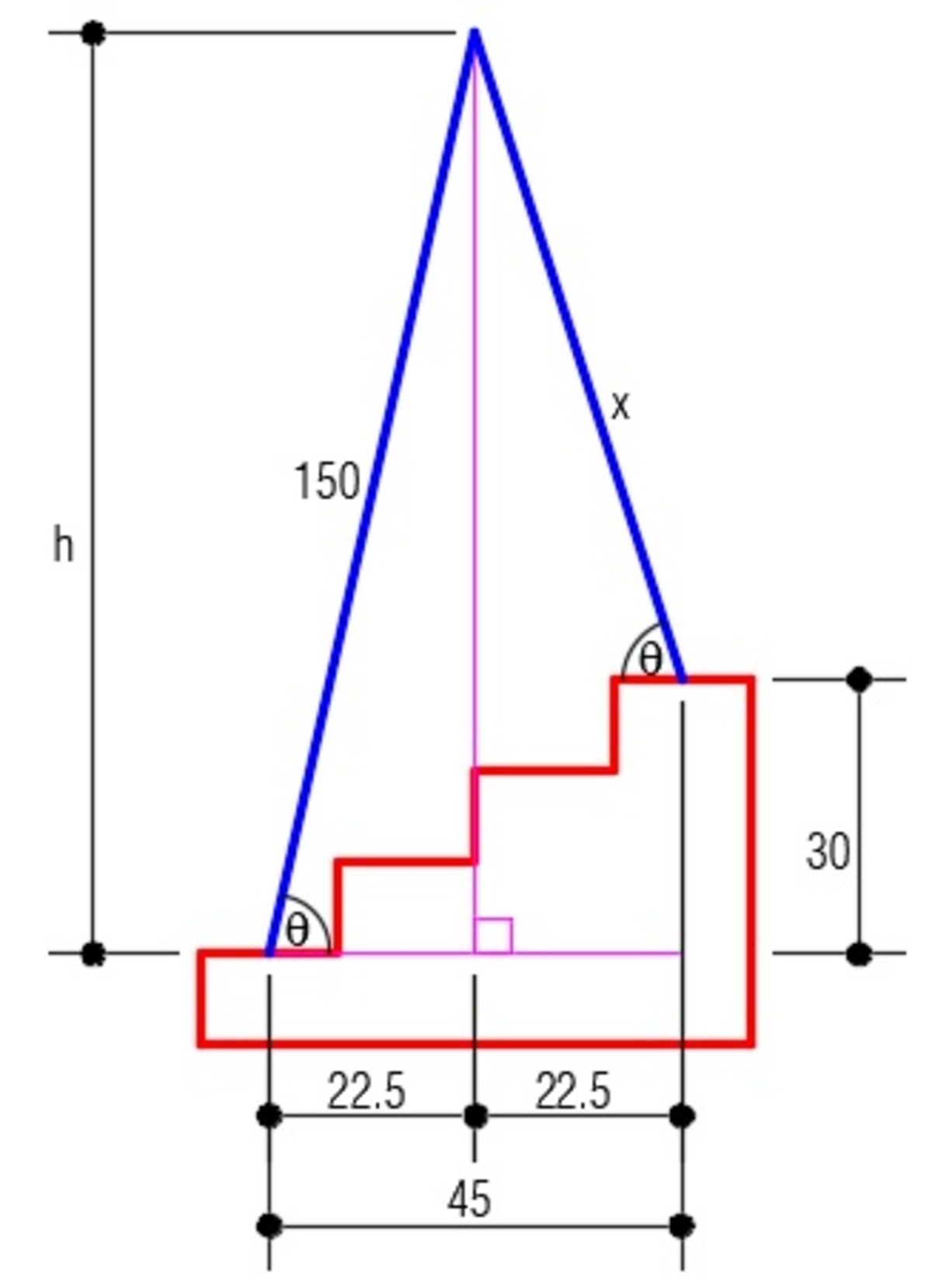 Consider my diagram. By pythagorean theorem,
h
=
1
5
0
2
−
2
2
.
5
2
=
2
1
9
9
3
.
7
5
Consider my diagram. By pythagorean theorem,
h
=
1
5
0
2
−
2
2
.
5
2
=
2
1
9
9
3
.
7
5
sin θ = 1 5 0 h = x h − 3 0 ⟹ x = h 1 5 0 ( h − 3 0 ) = 2 1 9 9 3 . 7 5 1 5 0 ( 2 1 9 9 3 . 7 5 − 3 0 ) ≈ 1 1 9 . 6 5 7
Where the "lines" touch they are close to the middle. So you could get rid of the diagonal element and then do the equation. There are 3 10-inch steps and 3×10=30 so subtract 30 from 150 and you get 120in.
Draw a perpendicular and then apply Pythagoras to both left and right triangles
Suppose if we extend the shorter leg up to the same level as that of bigger one Then vertical height adds on to 30units more.. and now we if could imagine up the scenario and take increased vertical height same as ladders extended length, it nearly Coincides (though it's not equal but for simplification) then as congruency angles would be same and so the opposite lengths. So, x+30=150; x=150-30=120.
The shorter length will nearly be equal to 120 units.
By Pythagoras, the height of the taller right-triangle shown is ( 1 5 0 + d ) 2 − 4 5 2 . Then by similar triangles we get an equation for d :
( 1 5 0 + d ) 2 − 4 5 2 1 5 0 + d = 3 0 1 5 0 − d , which can be solved numerically for d ≈ 1 1 9 . 5 7 3 .