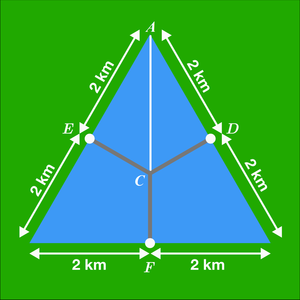
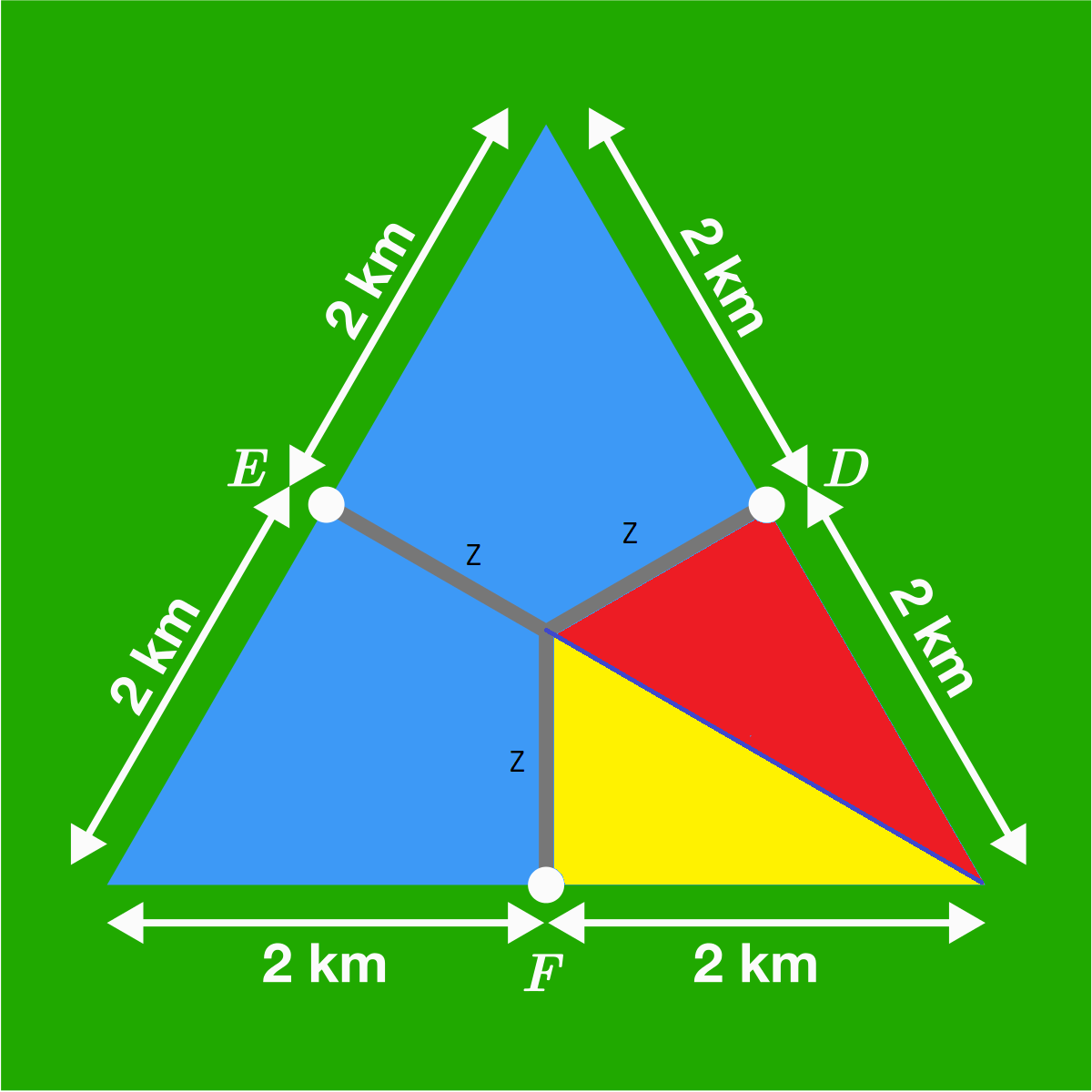
Lake Delta's New Highway
Architect Bob has designed a Y-shaped bridge across Lake Delta (in blue) to connect towns D , E , and F . The three arms of the bridge intersect at the centroid of the triangle.
What is the total length of Bob's bridge in kilometers?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
 It is known that for a triangle, the distance between the vertex and centroid is
3
2
of the length of median. That is
A
C
:
C
F
=
2
:
1
. By
Pythagorean theorem
the median
A
F
=
4
2
−
2
2
=
2
3
and
C
F
=
3
1
A
F
=
3
2
3
. Then, the total length of Bob's bridge
L
=
3
C
F
=
3
×
3
2
3
=
2
3
km.
It is known that for a triangle, the distance between the vertex and centroid is
3
2
of the length of median. That is
A
C
:
C
F
=
2
:
1
. By
Pythagorean theorem
the median
A
F
=
4
2
−
2
2
=
2
3
and
C
F
=
3
1
A
F
=
3
2
3
. Then, the total length of Bob's bridge
L
=
3
C
F
=
3
×
3
2
3
=
2
3
km.
I doubt you used the Pythagorean theorem as you know the ratios of sides in a 30-60-90 triangle.
Log in to reply
That's one way of solving the problem.
Log in to reply
Because that is an equilateral triangle,with many perfect qualities.
Log in to reply
@Zhang Hua – Yes, you can see my proof-without-word solution below.
i didn't know either of these 2 ( had heard about them but they sounded dumb so I didnt memorize them). but I saw that it was a triangle with al 3 sides being the same length. so angles are 60,60,60.
then looking at one of the 3 parts, I split it into 2 right triangles by drawing a line from the center to the corner. (just like the white line in the picture)
in which obviously pythagoras works: x=tan(pi/6)*2km
times 3 should give us the answer.
i turned it into a kite, and worked out angles first, then side lengths. don't think its easier or anything... just a different line of thought.
<cad=30 tan30=cd/ad so,cd=2/root3 total=3 2/root3 =2 root3
We can apply Viviani's Theorem to Architect Bob's highway:
The sum of distances of any point inside or on the side of an equilateral triangle is equal to the triangle's altitude.
Credit source: Wikipedia
In this case, the theorem takes the form
D P + E P + F P = A F
As A B C is an equilateral triangle, we can easily solve for A F with the information we have been given.
A F = A C 2 − C F 2
We input the value of A C , or 3 1 2 = 4 km.
A F = 4 2 − 2 2
A F = 1 2
A F = 4 ∗ 3
A F = 2 3
D P + E P + F P = A F = 2 3
We can therefore conclude that the highway's length, or D P + E P + F P , is equal to 2 3
Is there not a mistake in the 2nd equation : AF = \sqrt{AC^2 - CF^2} Could it be a mislabeling as CF is essentially what we are trying to solve for?
Log in to reply
There is no mislabeling, I think you mixed it with Chew-Seong figure. Place A on the top edge of the triangle, C on any base' edge.
Can there be some clarity in the question.... There is nowhere mentioned that the intersection point is on the centroid and all the bridges are perpendicular to their respective sides. All I did was to make a WILD GUESS.
Never heard of that theorem. Very cool simple solution.
Log in to reply
Log in to reply
Thank you. Great video, and even better channel! Never seen his vids before.
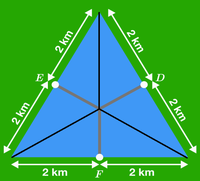
Add 3 line segments as shown to split the figure into 6 triangles. As the large triangle is equilateral and the bridges are perpendicular, each of the 6 smaller triangles is a 30-60-90 triangle.
By using the 30-60-90 triangle rule
( short side ) × 3 = ( medium side )
we can find each "arm" of the bridge is 3 2 . There are three of them, so the total length is: 3 2 × 3 = 2 3 .
I really liked this method of explanation. Thank you
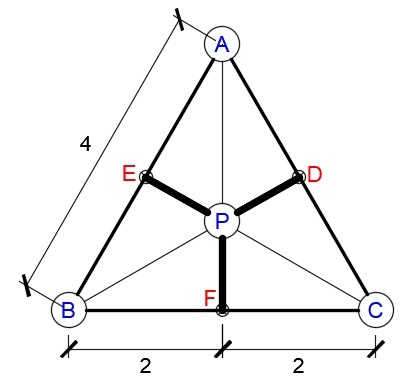 Note: All distances in the diagram are in kilometers.
Consider my diagram. By pythagorean theorem,
Note: All distances in the diagram are in kilometers.
Consider my diagram. By pythagorean theorem,
A F = ( A B ) 2 − ( B F ) 2 = 4 2 − 2 2 = 1 6 − 4 = 1 2 = 2 3
Note that P F = 3 1 of A F . So
P F = 3 1 ( 2 3 ) = 3 2 3
Since P F = P E = P D , the total length of the bridge is
P F + P E + P D = 3 ( P F ) = 3 ( 3 2 3 ) = 2 3 km
With minimal trigonometry involved, here is the good "proof-without-words":
Here,
G
E
,
D
G
and
F
G
are bolded to indicate that they are bridges. It suffices to extend more equilateral triangles to one of the three sides due to symmetry. In fact, we can see that all dashed segments have the congruent lengths.
which represents that
∣
F
A
2
∣
is both the sum of all bridge lengths and the combination of all three collinear segments
F
G
,
G
H
and
H
A
2
. Thus, elementary geometry shows that
sum of all three bridge lengths
=
∣
A
1
F
∣
×
3
=
2
3
I used trigonometry to solve this problem. I started by defining all of the angles that I needed, I then divided one of the sections of the lake in half, which gave me a right triangle (it has to be right because the lake is in the shape of and equilateral triangle). All of the angles in this triangle will be half of what they were before we split it, so now we have a triangle with angles of 30, 60, and 90 and a side length of 2. We need to find out what the side adjacent to it is, and to do this my process was the following:
tan(30)= 2 x
2tan(30)=x
x=1.5470...
3x=3.4641...=2√3
This is a simple way to solve this problem if trigonometry is more to your liking
Area of the triangle is A = 4 3 ∗ 4 2 . If we divide this by 3 we get the area of each of the three quadrilaterals delimited by the bridge. That is the sum of 2 right triangles that share the same hypotenuse (red and yellow), so its area is equal with the one of a rectangle with sides of z and 2 respectively.
Area of such rectangle is z * 2, therefore z = 2 ( A / 3 ) . So z = 3 2 3 . So the bridge length is z ∗ 3 = 2 3
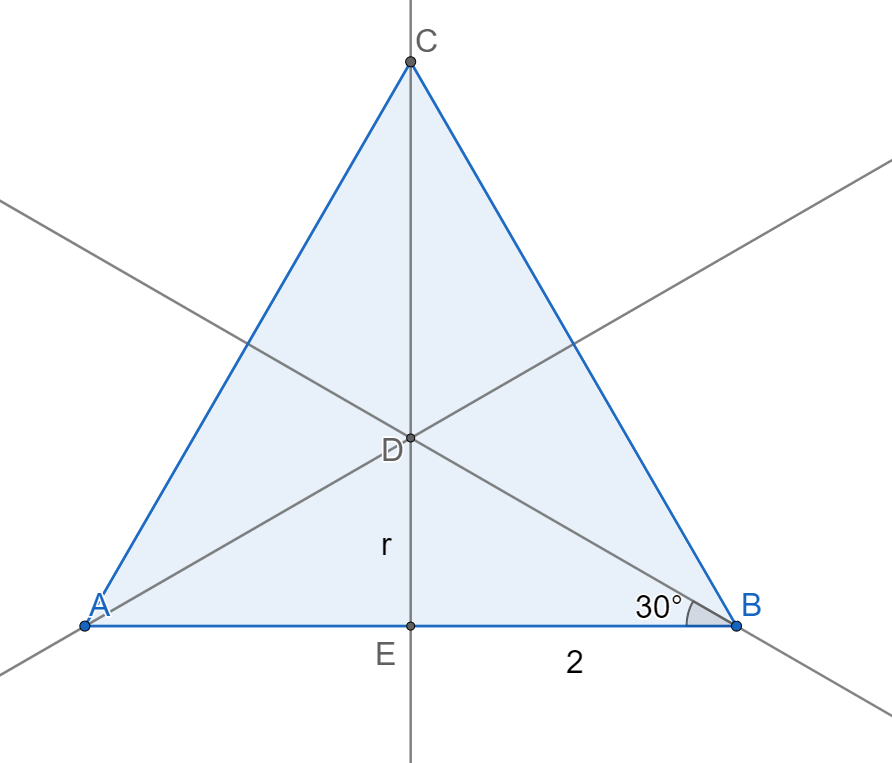
Let's take a look at the △ B D E .
tan 3 0 ° = 2 r
3 3 = 2 r
then r = 3 2 3
What he wants is 3 r then the answer is 2 3
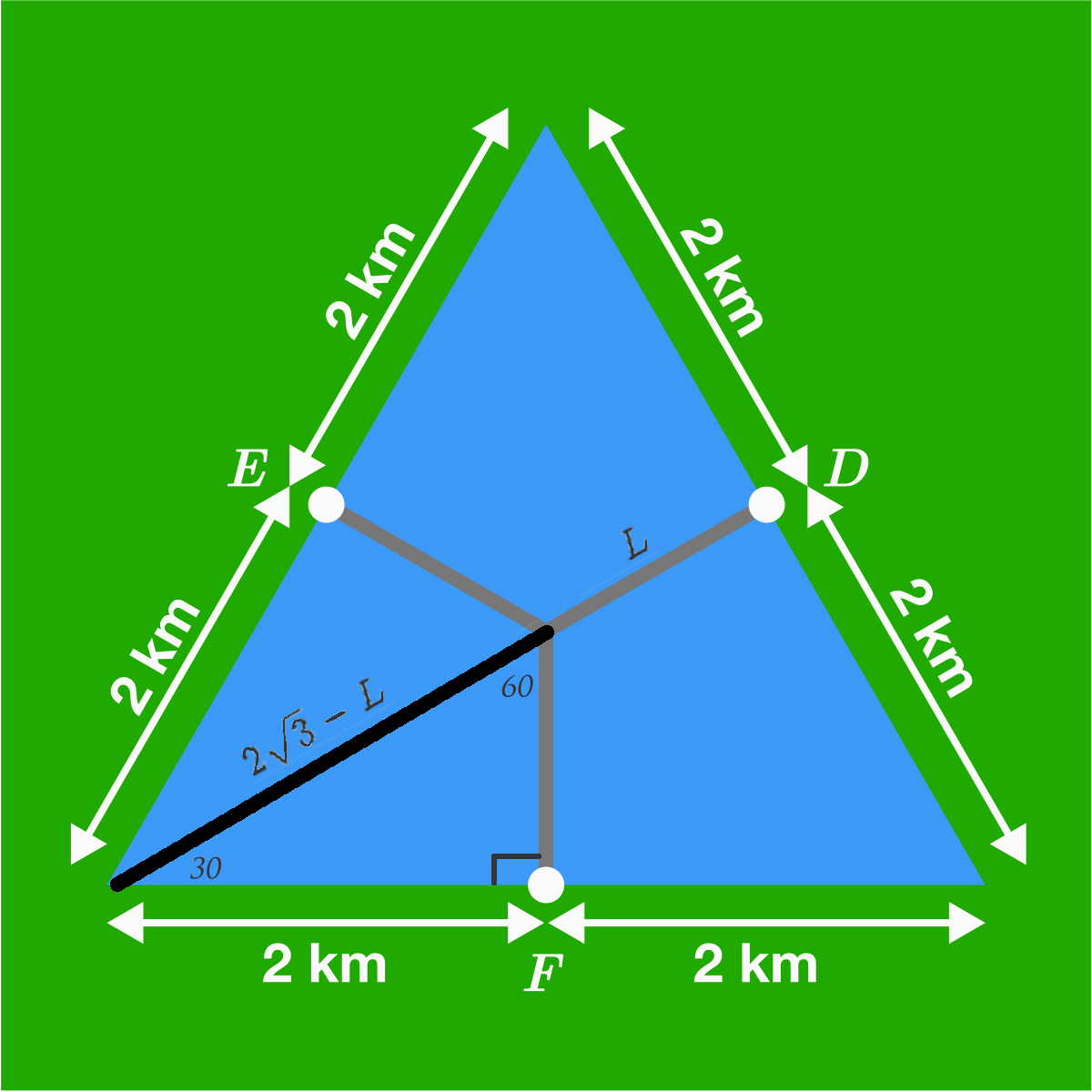
The altitude, A , of the triangle, is 4 sin 6 0 = 2 3 .
Create a small right triangle whose hypotenuse goes from a vertex to the center and whose altitude is one of the bridges.
Let L be the length of one of the bridges. The length of the hypotenuse of this small right triangle must then be A − L = 2 3 − L .
The equation for the altitude of the small right triangle, the length of the bridge, is L = ( 2 3 − L ) sin 3 0 .
Solving for 3 L :
- L = ( 2 3 − L ) 2 1
- 2 L = 2 3 − L
- 3 L = 2 3
So the sum of the lengths of the three bridges is 3 L = 2 3 .
Each part of the bridge is an inradius of the circle. The area of an equilateral triangle is 4 s 2 3 . The area of any triangle can be expressed as r s , where r is the inradius and s is the semiperimeter. With the first formula the area of the triangle is seen to be 4 3 . The semiperimeter is 6, so the inradius must be 3 2 3 . Multiplying by 3 gives 2 3 as the final answer.
While others have taken more efficient routes to solve this. I sometimes have trouble visualizing solutions using an entire shape, so I sliced it as follows:
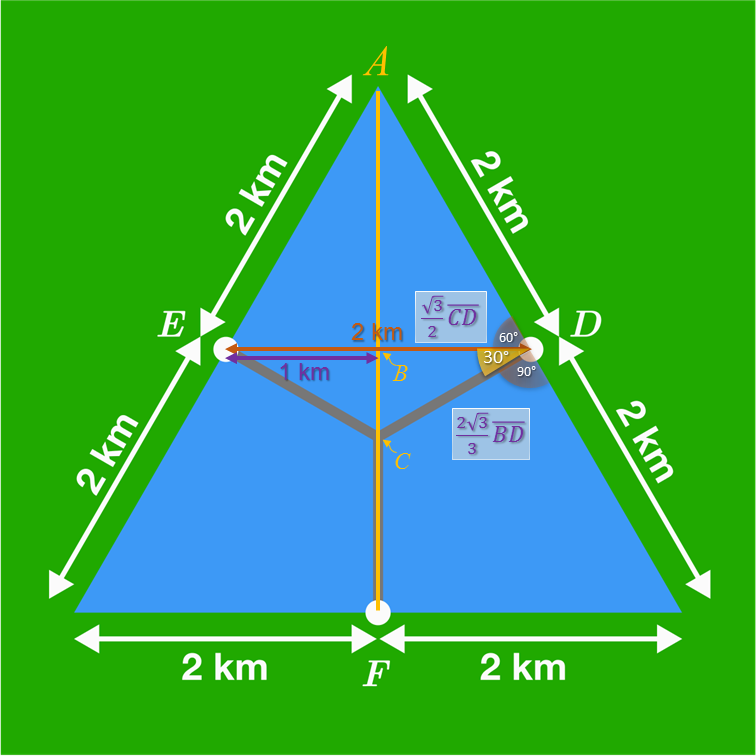
D E creates △ A D E with sides of 2 km. When bisected by A F , the length of resultant B D is 1 km.
∠ C D E = 3 0 ∘ which then means that B D = cos 3 0 ∘ C D = 2 3 C D
However, since B D = 1 , and cos θ = h y p a d j we must find the inverse of 2 3 and multiply it by the adjacent B D to find C D
This gives us 3 2 B D
As B D = 1 , C D = 3 2 ⋅ 1 = 3 2
There are three lengths of these "bridge sections", we find the total by 3 ⋅ C D = 3 ⋅ 3 2 = 3 6
Finally, this can be simplified by rationalization to find the solution in the multiple choice answers:
3 6 ⋅ 3 3 = 3 2 6 3 = 3 6 3
= 2 3 (km, of course)
- In fact this problem is the same meaning to ask what the 3 times of this triangle's inner circle's radius. So we can just calculate how much is the radius of the inner circle.
First, we recognise each arm of the bridge as the radius of the inscribed circle. The area of the triangle in terms of the radius of the inscribed triangle is: A = 2 1 r ⋅ ( perimeter of triangle ) = 2 1 r ⋅ 3 a Where we denote a the length of a side of the triangle. Use Pythagoras to find the altitude of the original triangle (from corner to opposite endpoint): h 2 = a 2 − 4 a 2 ⟹ A = 2 1 a h = 2 1 a a 2 − 4 a 2 Hence: 3 r = a 2 − 4 a 2 = 1 6 − 4 = 2 3 But 3 r is simply the length of the bridge...
Using sin rule Sin60/2 = sin30/x where x is 1 bridge Cross multiply .866x=1 X=1.15 3 brigdes = 3.46
I forgot whatever formulas there may be for figuring this out, I just kept breaking one 1/3 section into smaller triangles and using simple trig to eventually figure out what each length of the bridge should be, then of course multiplied by 3.
it can be simply done by using trigonometry, Consider the centroid be C, any of the vertices be V and the point where one of the arms of the bridge is touching the side of the equilateral 🔺 be S. Now the points C, V, and X form a right angle 🔺 ,of angles 30 and 60 degree . By simply applying the tangent formula, You will get the length of one arm of the bridge to be 2/root3, multiply this by 3 because there are three sides of the bridge. You will get the answer 2root3.
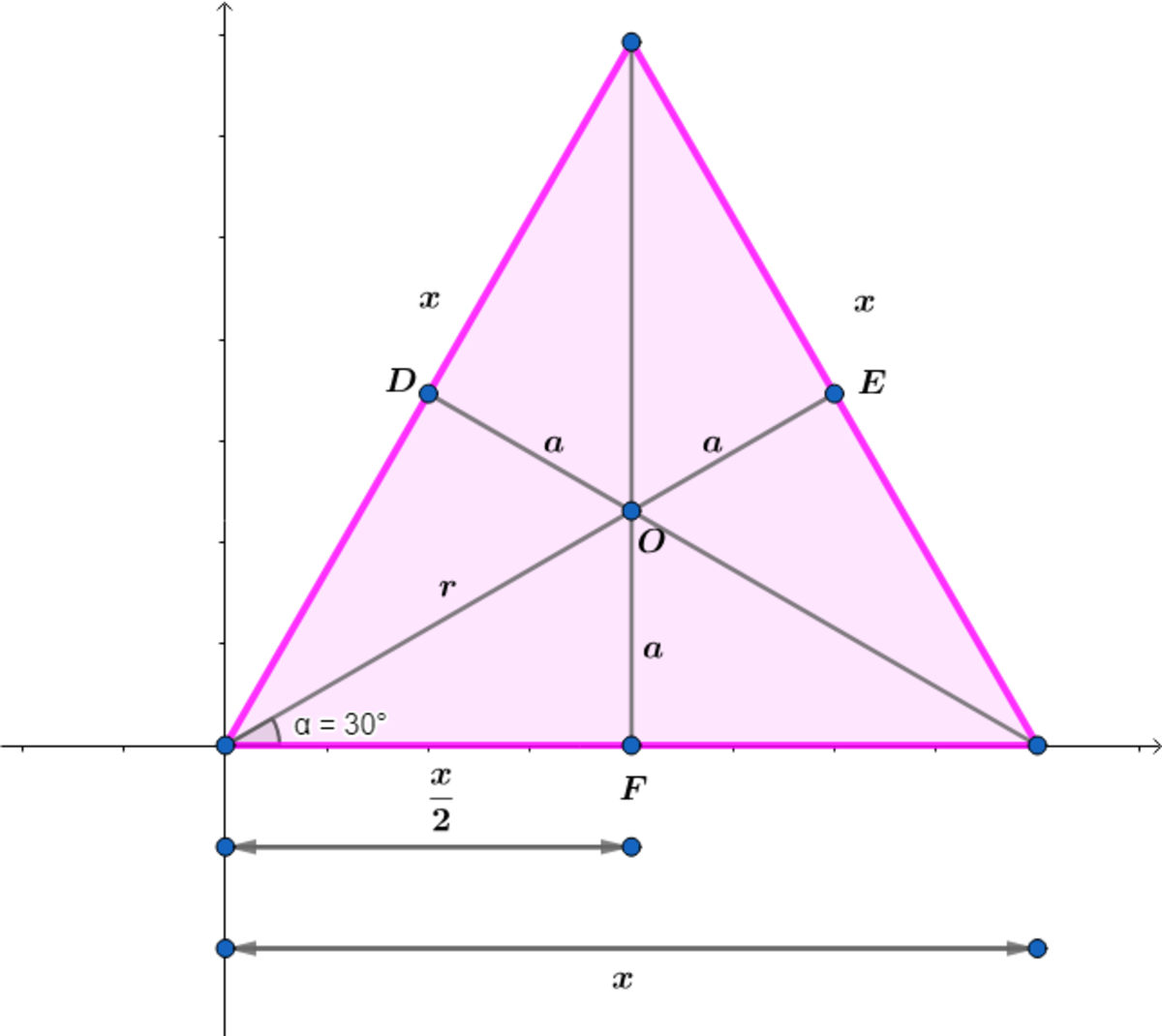
2 x = 2 3 r ⟹ r = 3 x ⟹ a = 2 r = 2 3 x ⟹ Total Length = 3 a = 2 3 3 x = 2 3 x .
x = 4 ⟹ Total Length = 2 3