Large Sides Means Large Area, Right?
Which of the following triangles has a larger area:
- triangle A with side lengths 1 3 , 1 3 , 1 0 , or
- triangle B with side lengths 1 3 , 1 3 , 2 4 ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
Nice! The diagram makes it really obvious :)
Wow, I did it with Heron's formula and took forever. It goes to show that drawing diagrams should be the first step.
Of course that's from where the numbers were similar you just needed to know that 5^2 + 12^2 = 13^2, beautiful solution.
I did it the same way, but I wonder if you or someone would be good enough to tell me how to include diagrams in a solution that I post (which would be very helpful in a solution of the side-length of a square that I posted, though without a diagram). Regards, David
Log in to reply
On desktop, the is a toolbar when you're submitting a solution. Clicking on the third icon from the left allows you to upload an image to be displayed.
Note: We use markdown formatting, so if you already have the image uploaded, you can just type in

.

I don't like this problem statement much. The fact that it doesn't mention what units of length made me figure this was indeterminate. i.e. one could claim the first triangle was inches, the second in cms or some such. Tony
Log in to reply
If units are not specified, then the (unwritten) assumption is that they are in the same units.
Wow it take me so long to get the hag of this
actually, it should be 5*12 divided by 2, which is 30
Log in to reply
Remember that each original triangle comprises 2 of these 5-12-13 right triangles, which is why the formula wasn't divided by 2.
"S" means "semi-perimeter", not "squared area" or something, as it may look.
By Heron's formula:
Triangle A:
S 1 = 2 1 3 + 1 3 + 1 0 = 2 3 6 = 1 8
Area ( A 1 ) = S ( S − a ) ( S − b ) ( S − c ) = 1 8 ( 1 8 − 1 3 ) ( 1 8 − 1 3 ) ( 1 8 − 1 0 )
= 1 8 × 5 × 5 × 8
= 2 × 3 2 × 5 2 × 2 3
= 2 4 × 3 2 × 5 2
= 2 2 × 3 × 5 = 4 × 1 5 = 6 0
Triangle B:
S 2 = 2 1 3 + 1 3 + 2 4 = 2 5 0 = 2 5
Area ( A 2 ) = S ( S − a ) ( S − b ) ( S − c ) = 2 5 ( 2 5 − 1 3 ) ( 2 5 − 1 3 ) ( 2 5 − 2 4 )
= 2 5 × 1 2 × 1 2 × 1
= 5 2 × 1 2 2 × 1 2
= 5 × 1 2 × 1 = 6 0
A 1 = A 2 = 6 0
Thus, the answer is E q u a l
Yeah I use the same method with you, it is easy!
Exactly the way I have done! It is the best way
Log in to reply
Hardly the best way.
Log in to reply
Yeah come on that was me 2 years ago; (I think it was when I started learning to solve problems in a beautiful way) :)
The first method is easy the triangles are both right triangles with side lengths (5,12,13).But if you didn't realize that First find the length of the height and then you are going to realize that the base and the height are the same for the two triangles proving that the area would be same.The length and base should be be 12 and 5 in both triangles. In advance you could use herons formula
I click wrong lol...but using logical thinking it's equal....no need calculation at all....
Log in to reply
hello, can u explain it? ..I used Heron's formula, but logical way is most interesting, so please. :)
Log in to reply
I don't know what is herons' formula haha....triangle's formula is 1/2 times base times height ....you draw it out or imagine it using 13 as base and height....sub into formula it would be just the same.....because hypothenuse isnt the main point in the formula i guess...
no it is correct
using heron's formula it would be simple
Log in to reply
I disagree. This method is obviously faster, more elegant and relies on less calculation.
how it is? please explain it briefly
Log in to reply
Heron's formula:
Area of a triangle = under root of s(s - a) (s - b) (s - c)
where S is half the perimeter of the triangle and a, b, c are sides of the triangle. Use this on both the triangles and you'll see that both areas are equal to 60
You can refer my solution.
This solution by Mardokay is good. Only, it doesn't always strike us that we should probably see if the sides happen to be a pythagorean triplet. Heron's formula strikes first.
Dont understand fully. As far as i know, the area of triangle is 0.5 x width x height.
And normally the numbers given are l x w x h ....so height would be 10 and 24 and therefore not the same area ?
What am i missing/overseeing in this assumption ?
Thanks, Bent
But how can you figure out the height?
Check out the 5:12:13 right triangle in both cases.
Michael Mendrin : Yours is by far the easiest and shortest method. Pooja Nath's solution - by using diagrams - explains where the 5:12:13 triangles come from.
Thumbs up!
You should send your peers over to Brilliant so that they can learn from the community!
Log in to reply
I sent some already on here and others...well...if math was a person, they would run away from it.
Log in to reply
I promise I won't bite.
Yea I understand. But that's cos they haven't done been on Brilliant :)
Log in to reply
@Calvin Lin – I know you don't bite. A few of my peers did practice from my EOC sets that I did. I will be finishing the Geometry EOC set though since I have gotten some notices from people to finish it.
Log in to reply
@Lew Sterling Jr – That's really exciting!
Log in to reply
@Calvin Lin – Yeah. I have about 30-40 questions I got to do for the Geometry EOC set.
I cant picture it because the with is 24, much wider than 10. since they have two 13 side i can picture out that they are not equal. so cool.
isn't that a semiperimeter not a perimeter ?
Very easy use herons formula
Triangle A. (Semi perimeter=18) area=√18(18-13)(18-13)(18-10) =√18 5 5*8 =√3600 =60
Triangle B (semi perimeter =25) Area=√25(25-13)(25-13)(25-24) =√25 12 12*1 =√3600 =60
- draw a construction line perp from mid of the base of the triangles,
- find the height of a triangle and simply
-
then apply formula of area of triangle, as A= (Height x Base)/2
for both the triangle the procedure used is same and then - campare the both Areas of a Traingle
The height of an isosceles triangle can be calculated by using pythagoras theorem. Consider the unequal side as the base. One of the equal sides and half of the length of the unequal side and the height form a right triangle. The equal side serves as the hypotenuse.
Hence, Square(Equal Side)= Square(Height) + Square(Half of Base or Unequal Side)
Thus, for each of the triangles, Height = 12 , Base = 10 and area = 60 (Triangle 1) [square(13)=square(12-height)+square(5-half of base)] Height = 5, Base=24 and area=60 (Triangle 2).[square(13)=square(5-height)+square(12-half of base)]
Therefore the triangles have equal area.
In an isosceles triangle the altitude bisects the dissimilar base.
Use c^2 = a^2 + b^2 to solve for the altitudes.
Then find the areas. They both equal 60.
only one property of an isosceles triangle can make this just a two lines sum........that is the perpendicular when dropped on the base divides the base into two equal parts.............in the first triangle.half of the base is 5 and its ht is 12.............in second triangle.half of the base is 12 and its ht is 5............now area of a triange is 1/2.base .altitude value of whose is same for both triangles ........thats it...........!!!!!!!!
In the figure below, the vertical to the base of the isosceles triangle,
h
= sqrt(a^2-(b/2)^2).
The area of the triangle is (h * b) / 2 = (sqrt(a^2-(b/2)^2) * b) / 2.
Replacing
a
with 13 and
b
with either 10 or 24, the result is always 60.
Think about Pythagorean triples! (5,12,13) is a triple so it immediately gives the answer.
I want calculus language.
Bisect them and you get two triangles, 5-12-13 on the sides.
Both are isosceles triangle. For triangle A find height =sqrt(13^2 - 5^2) =12, so area of triangle 'A'= 1/2 (base)(height)=1/2 (10)(12)=60; for triangle 'B' height= sqrt(13^2 - 12^2)=5, hence area of 'B'=1/2(24)(5)=60.
Use heron's formula and find out
Use Heron's Formula. Most Mathematical to Prove!!
it is very is problem with some calculation by determine area using heron's formula. s=\frac{a+b+c}{2}. A = \sqrt{s(s-a)(s-b)(s-c)},
Heron's Formula
Bashed it out with Heron's. I'm not sure exactly why, but somehow they are equal. :D
Take two 5-12-13 triangles. Put them together on the 5 face.
Take two more 5-12-13 triangles. Put them together on the 12 face.
Do you see now?
Another [cryptic] hint on why they are equal sin θ = sin ( π − θ ) .
Both the triangles are isosceles triangles, which means that median of the triangle on the non-equal side is also the normal. We have two pictures now: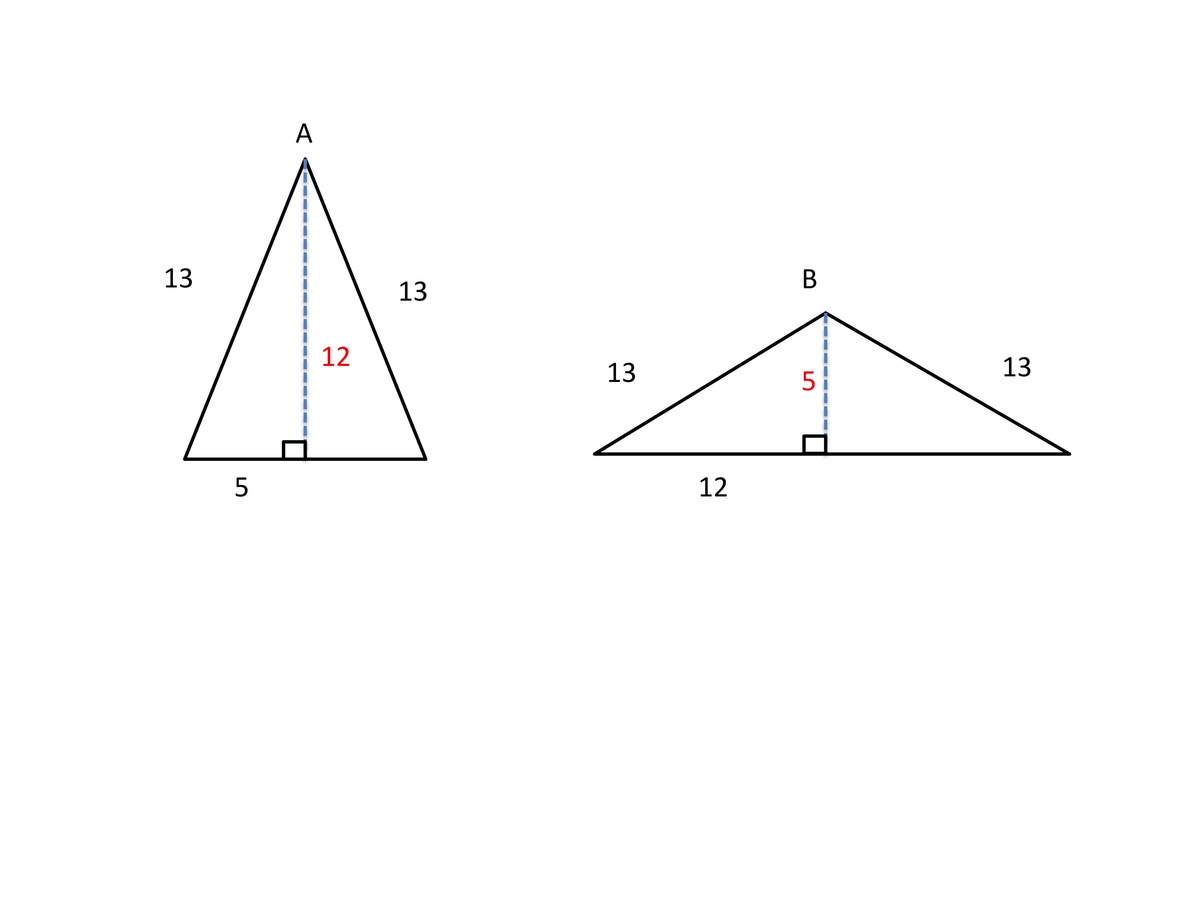
Thus both the triangles have the same area now, which 12*5 = 60 sq units.