Largest Square in Triangle
Given a triangle with vertices ( 0 , 0 ) , ( 1 6 , 0 ) , ( 6 , 8 ) , find the length of the side of the largest square which can be inscribed in it. If the length is expressed as q p where p and q are coprime positive integers, submit p + q .
The answer is 377.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Let
s
a
,
s
b
and
s
c
be the sides of the squares inscribed in the triangle and having one side on
B
C
=
a
,
C
A
=
b
and
A
B
=
c
, respectively.
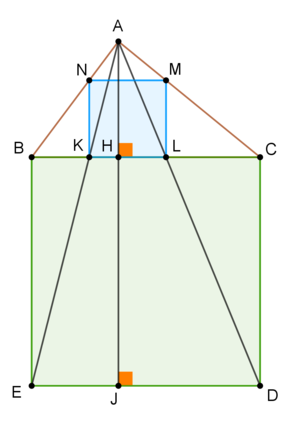Referring to the figure, triangles
△
A
K
L
and
△
A
E
D
are similar, hence the ratio of their sides equals the ratio of their respective altitudes, i.e.
E D K L = A J A H ⇒ a s a = h a + a h a ⇒ s a = h a + a a h a ⇒ s a = a 2 A + a 2 A
Likewise, s b = b 2 A + b 2 A Comparing the sides of the two squares we have
s a ≥ s b ⇔ a 2 A + a 2 A ≥ b 2 A + b 2 A ⇔ a 2 A + a ≤ b 2 A + b ⇔ ( b − a ) ( a b 2 A − 1 ) ≤ 0 ⇔ ( b − a ) ( a b a b sin C − 1 ) ≤ 0 ⇔ ( b − a ) ≤ 0 ( sin C − 1 ) ≤ 0 ⇔ b ≥ a This means that the biggest square is the one that lays on the smallest side of the triangle. In our case, it is the square on the side of length 10.
Log in to reply
Let s a , s b and s c be the sides of the squares inscribed in the triangle and having one side on B C = a , C A = b and A B = c , respectively.
But that's the thing: How do we know that the largest possible square inscribed has all 4 of its vertices touching the edges of the triangle? Why can't it be 3?
This means that the biggest square is the one that lays on the smallest side of the triangle. In our case, it is the square on the side of length 10.
Wouldn't this disprove your claim?
Also, what app did you use to design such lovely geometry figures?
Log in to reply
A quick answer to your second comment (I had to expect you would notice it): Yes, my claim holds just for the case of an acute triangle, like the one Fletcher gave. Otherwise there is no square inscribed in the triangle having all four vertices on the sides of the triangle, with two of them on one of the sides of the obtuse angle. For the figuresI use Geogebra. For your first comment, I need some time...
@Pi Han Goh - Hi! I think you might be interested in this . I have posted a solution there, that gives the answer to your question about the posisioning of the largest square in the triangle.
Log in to reply
Wow, I'm going to spend at least an entire afternoon reading your essay. Thanks!
Log in to reply
I couldn't make it shorter :) At least I hope my response to your challenge settles things out.
Log in to reply
@Thanos Petropoulos – Yay! You're now my 3rd favorite person on this site!
Log in to reply
@Pi Han Goh – @Pi Han Goh - Oh, I'm trully honored! Thank you!
Disclaimer: This solution is incomplete. I did not prove that "The largest square inscribed must have one entire side touching a side length of a triangle."
Suppose the largest square lies flat on the base of this triangle. A simple plot on Desmos tells us that the side length of the inscribed square is 5 3 1 . But can this be beaten?
If we use this tool , we will see that the side length of the largest square is not parallel to the x -axis.
In fact, the coordinates of the triangle do not actually matter. Using the distance formula, the triangle has side lengths 1 0 , 1 6 , 1 6 4 .
Without the loss of generality, I can replot the coordinates of the triangle as ( 0 , 0 ) , ( 1 0 , 0 ) , ( 5 4 8 , 5 6 4 ) .
Since I'm lazy to redo the same approach in the Desmos above, I used Calvin Lin's 2nd way to draw squares Inside triangles here (with the timestamp attached) . We have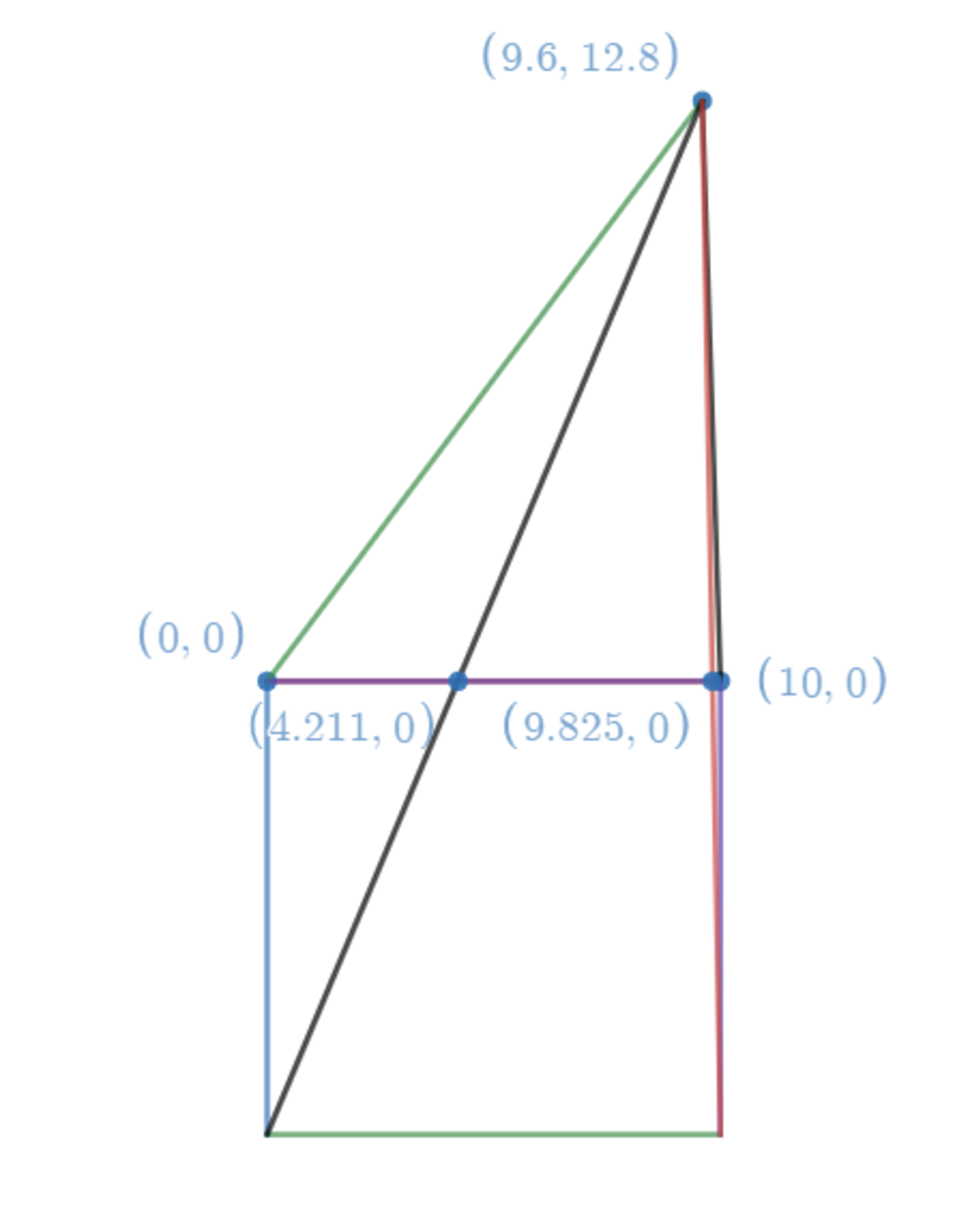
as shown in my other Desmos mini project .
And the side length of this square is 5 7 5 6 0 − 1 7 8 0 = 5 + 3 7 3 5 = 5 7 3 2 0 which makes the answer 3 2 0 + 5 7 = 3 7 7 .
Now, can someone prove that the square we've found is indeed the largest?