Last problem of the year!
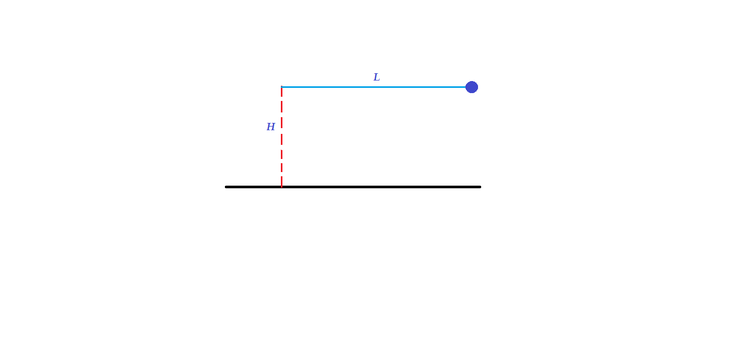 is a fixed point at a height
above a perfectly inelastic smooth horizontal plane. A light string of length
(
) has one end attached to
and other to a heavy particle. The particle is held at the level of
with string just taut and released from rest. Find the height of the particle above the plane when it is next instantaneously at rest.
is a fixed point at a height
above a perfectly inelastic smooth horizontal plane. A light string of length
(
) has one end attached to
and other to a heavy particle. The particle is held at the level of
with string just taut and released from rest. Find the height of the particle above the plane when it is next instantaneously at rest.
This question is from the book DC Pandey .
Also try this . :)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Just before the particle collides with the ground, it will have a speed 2 g H and the string will make an angle
θ = arcsin ( L H )
Since the ground is inelastic and horizontal, the vertical component of that speed will be lost, and the particle will then be traveling along the ground with a speed of
V g r o u n d = 2 g H sin ( θ ) = L H 2 g H
The particle will travel along the ground to the other side of A and eventually the string will again make an angle θ with the ground. Since the string is presumably inextensible, the particle will lose all of it's speed in the direction parallel to the string. Therefore immediately after the string becomes taut and the particle begins to leave the ground, it will have a speed of
V g r o u n d sin ( θ ) = ( L H ) 2 2 g H
From now on, the string only applies a force perpendicular to the particle's motion, so energy is conserved and we can write the equation
2 m ( ( L H ) 2 2 g H ) 2 = m g x
Which means
x = L 4 H 5