Last Whole Piece

The animation to the right implies that we can eat an infinite amount of chocolate from the same chocolate bar, but it is misleading—after each reassembly of the chocolate bar, the height of the chocolate bar actually decreases slightly.
Suppose you kept on cutting, taking out one whole piece while reassembling the remaining pieces into a solid rectangular bar without holes . How many whole pieces can be taken out in this way?
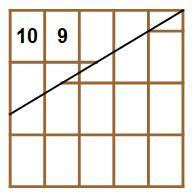
Let the number of whole pieces removed from the bar—out of the ten pieces labeled 1 to 10 below—be n , and let the number written on the last piece removed be x .
What is n x ?
Details and Assumptions:
- At the start, the sloping cut passes through the bottom right corner of piece 9, so that all the pieces below it stays the same each time the cut pieces are reassembled.
- Each reassembly is done with 3 cut pieces (out of 4), as in the animation, along and above the red, dotted line. Remember, 1 labeled piece is always eaten up after each reassembly.
- If after taking out a whole piece, the remaining pieces cannot be reassembled into a solid bar without holes, that piece does not count.
The answer is 64.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The idea of stopping at stage 8 is hoping the kids won't notice.
Thanks for sharing that drawing of the whole thing. Clear cut, you might say.
Log in to reply
I saw this problem in the Community section last week and your questions confused the heck out of me so I didn't touch it. I've seen this type of geometry trick many times so that wasn't a problem. It was only when I started drawing it that I realized what you were asking.
The problem itself is great and I think the wording is fine. It's just a tough challenge.
Log in to reply
Jeremy, your contributions to Brilliant.org have been valuable and I appreciate the input you've provided in some of my problems. Is there a way you can contact me to ask about the wording of my posted problems? I'm alway concerned about how understandable my problems are.
Log in to reply
@Michael Mendrin – What we need is a better way to comment on problems without having to "report" them. Sometimes a problem is ok but could be worded better.
Log in to reply
@Jeremy Galvagni – I completely agree with you. What if we created a Note for discussion on wording of posted problems?
Log in to reply
@Michael Mendrin – Precisely. when you click the "more ..." at the lower right of a posted problem there could be a "note" or "suggestion" along with "report." This could be a private note, since a report is public.
u ruined my dreams of infinite chocolate :-(
There is a magic unnumbered, but full width piece of chocolate next to block #10 that appears then disappears then appears again and then another unnumbered full width piece is added, so what does "without holes" mean?
Log in to reply
Jeremy is re-coloring the pieces before they are moved around. Only in the last stage does a hole appear. None of the pieces themselves are cut up, they're just moved around.
All of the pieces move around a bit. That particular one with the tiny corner missing starts next to the 10, but after cutting and reshuffling, it is under 7 in stage 2. It ends up next to 10 again in step s 3. (Interesting) It stays next to the 10 until stage 7 where it's under the 8. Then it's next to the 9 again. In the last picture, it is the one that forms the hole.
We can see how many times we can cut out a piece by looking at how much each rearrangement shortens the height. We will label the amount that the diagonal line rises (per square)
x
as shown in the first picture.
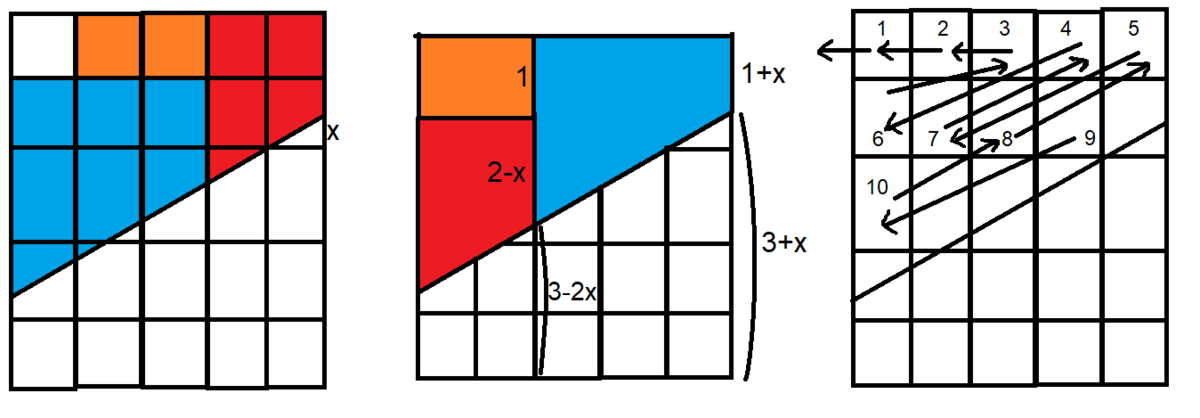
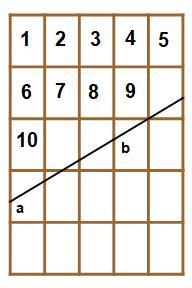
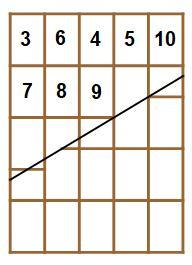
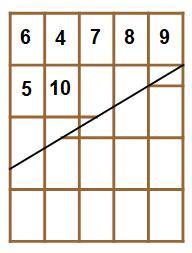
As we can see from the second picture, in order for the resulting rearrangement to form a rectangle we must have 1 + 2 − x + 3 − 2 x = 1 + x + 3 + x ⟹ x = 5 2 . We can also see that the section on the top of the right edge changes from 2 − x to 1 + x , a loss of 5 1 each rearrangement. We started with an available height (on the top section of the right edge) of 5 8 , and we lose 5 1 each rearrangement, so we can rearrange 8 times. The third picture is a graph of what happens to each piece every rearrangement. Thus we just need to count backwards around the graph 8 steps (starting with the first piece) to find out which piece is the last one removed. The pieces are removed in this order: 1 , 2 , 3 , 6 , 4 , 7 , 5 , 8 so we have square 8 removed after 8 steps giving an answer of 6 4
The sequence of whole pieces that can be cut from this is 1 , 2 , 3 , 6 , 4 , 7 , 5 , 8 and still leave behind a solid rectangle.
If the dimensions of one of the chocolate pieces are
1
wide by
2
3
high, then the slope of the cut in black has to be
5
3
.
Notice that corner b of one of the pieces is going to move to corner a , while the top of that piece must drop by 2 3 + 1 0 3 = 5 9 in order to drop the height of the reassembled bar by 1 0 3 which results an area deficit of 2 3 , the area of one piece. This is the reason why the slope must be 5 3 . See the following figures, each time the height of the reassembled bar dropping by 1 0 3 . None of the whole pieces and the partial pieces at the start are ever themselves divided in subsequent cuttings, they are just rearranged. The partial pieces are rotated cyclically by 2 with each reassembly.

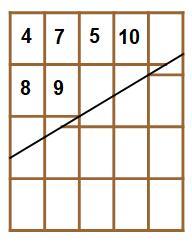
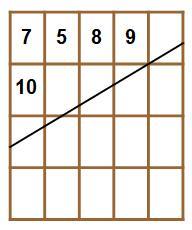
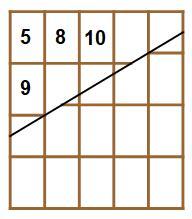
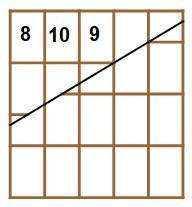
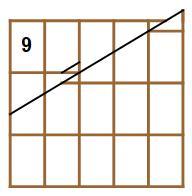
Based on the question, "a solid rectangle without holes", we know:
1.It can't have holes (which the animation gives us a good way to avoid that)
2.It has to be a rectangle.
So when does it stop being a rectangle?
It will seem good UNTIL the Right most side of the top section is Gone and the Top Line of the top section is below the top right corner of the bottom section, like the stage 9 picture that another good answer illustrates.
One Key thing in order to solve the problem: When the you reassemble it, notice that the left edge of the left big chunk and right side of the right big chunk has to match, otherwise they will have a height dismatch, therefore not a rectangle any more.
Therefore the left most of red dotted line and the right has exactly a two-row-of-chocolate difference,
Therefore the intersection between red line and the chocolate row line should be in the about-center of the chocolate horizontally, AKA the about-center of the third column WHEN the top section becomes a triangle or almost-triangle,
Therefore there would be 2 bars left(the top left two)
Then you can count the order of eating.
OVER
I started drawing successive stages to get a feel for how the pieces moved. Even though I had it figured out before drawing the whole thing, I thought it would be a nice picture to share. So I finished it and here it is.
After each stage I recolored the pieces before shuffling and removing a bite of chocolate.
On stage n = 8 we remove the piece x = 8 so n x = 6 4