Lattice Fog

Relevant wiki: Riemann Zeta Function

First imagine that we are standing at the origin, and that the grid is that of the lattice (integer) points.

The point $(4,6,2)$ is not visible because the point $(2,3,1)$ is "in the way", and the point $(6,3,9)$ is not visible because the point $(2,1,3)$ obscures it.

We see that a point $(x,y,z)$ is not visible precisely when there is another lattice point blocking it, which is when there is an integer triplet $(x',y',z')$ such that $(x,y,z)=(kx',ky',kz')$ .

Equivalently, $(x,y,z)$ is not visible precisely when there is an integer $k$ dividing the trio $x$ , $y$ and $z$ , and is visible when there is no such integer, i.e. when $x$ , $y$ and $z$ have no common factor.

We can now state our question differently: For three random integers $x$ , $y$ and $z$ , what is the probability that they have no common factor?

For this to happen, it must be the case that no prime number $p$ divides $x$ , $y$ and $z$ . For a particular prime $p$ , the probability that $x$ is divisible by $p$ is $\dfrac{1}{p}$ , and the same for $y$ and $z$ , so the probability that the trio are divisible by $p$ is $\dfrac{1}{p^3}$ , and so the probability that $p$ does not divide the trio is $1-\dfrac{1}{p^3}$ .

The probability that no prime divides the trio $x$ , $y$ , $z$ is therefore

$\begin{aligned} \displaystyle & =\left(1-\dfrac{1}{2^3}\right)\times\left(1-\dfrac{1}{3^3}\right)\times\left(1-\dfrac{1}{5^3}\right)\times\left(1-\dfrac{1}{7^3}\right)\times\left(1-\dfrac{1}{11^3}\right)\times\cdots \\ & =\prod_{p \text{ prime}}\left({1-\dfrac1{p^3}}\right) \\ & =\left(\prod_{p \text{ prime}}{\dfrac1{1-p^{-3}}}\right)^{-1} \\ & =\left(\sum_{n=1}^\infty{\dfrac1{n^3}}\right)^{-1} \\ & =\boxed{\dfrac{1}{\zeta(3)}\approx 83\,\%}\end{aligned}$

---

Click here to see the proof that ${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\prod _{p{\text{ prime}}}{\frac {1}{1-p^{-s}}}}$

Related numberphile video:
https://www.youtube.com/watch?v=p-xa-3V5KO8

you can start at 9:35 to skip to the relevant section

First, considering the 2-D case. Fix a point e consider this as the origin $O$ of a cartesian reference frame. A point $P = (x,y)$ is visible from the origin $O$ only if the $GCD(x,y) = 1$ or equivalent $x$ and $y$ are co-prime. If the $GCD(x,y) = m > 1$ then there are other m-1 points on the same direction of P that are less distant from O than P (see figure below)

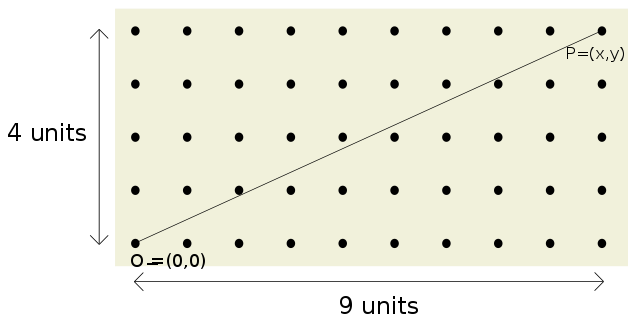
In the 2-D case the frequency of 2 coprime numbers can be calculated in the following way

Given a number $x$ , the probability that can be divisible by a prime number $p$ is $1/p$ . Since x and y are chosen indipendetly, the combined probability that x and y are divisible for p is the product of the single probability. Then

$P(x|p \cap y|p ) = P(x|p)P(y|p)= 1/p^{2}$

so the probability that x and y are not divisible by p is $1-1/p^{2}$ .

The probability that x,y are coprime is the probability that both x and y are not divisible by any prime number $p$ then

$P( x \text{ and } y \text{ are coprime}) = \prod_{\text{prime } p }^{} \left (1- \frac{1}{p^{2}} \right )$

This infinite production is equal to $1/ \zeta(2) = 6/\pi^{2}$ where $\zeta (z)$ is the Riemann zeta function (see Coprime Numbers )

Since for a infinite number of trials, the probability of a event tend to be the frequency that this event happen (see [Law of large numbers] )(https://en.wikipedia.org/wiki/Law of large_numbers)

In the 3-D case the condition that given a point $O=(0,0,0)$ , another point $P =(x,y,z)$ is visible from O is that the x,y and z are coprime. So generaling the formula above the probability that x,y and z are coprime is

$P( x, y \text{ and } z \text{ are coprime }) = \prod_{\text{prime } p }^{} \left (1- \frac{1}{p^{3}} \right )$

This infinite production is equal to

$\frac{1}{\zeta(3)} = \frac{1}{\text{1.202056....}} = \text{0.83}$ *

Then the percentage of points that are visible from a given point in the infinite lattice is $\boxed { \textbf{83\%} }$

paragraph 1

see Apery constant for more details about $\zeta(3)$