Let it roll
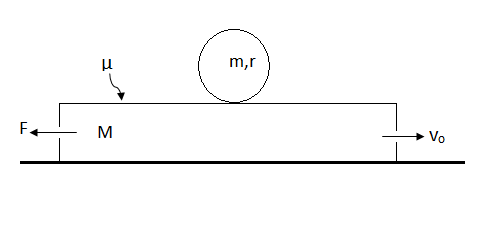
A plank of mass is moving on a smooth horizontal surface with speed . At time , a sphere of mass and radius is gently placed on it and simultaneously. A constant horizontal force is applied on the plank in the opposite direction of . Find the time at which sphere starts pure rolling on the plank . The coefficient of friction between the plank and sphere is .
, , , , , .
The answer is 0.147.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
F.B.D of sphere for no vertical acceleration N = m g
⇒ f = μ m g (as f = μ N )
⇒ a = μ g
v = μ g t , Also α = I μ m g r ⇒ ω = I μ m g r t where I is moment of inertia.
The velocity of the lower most point of the sphere at time t is
v s = v + ω r
v s = μ g t + I μ m g r 2 t
From F.B.D of plank
⇒ a p = − ( M F + f ) = − ( M F + μ m g )
v p = v o − ( M F + μ m g ) t
For no slipping v s = v p
⇒ μ g t + I μ m g r 2 t = v o − ( M F + μ m g ) t
as I = 5 2 m r 2
⇒ t = 2 7 μ g + ( M F + μ m g ) v o