Let's circulate again
How many real numbers I are there such that I = ∮ C x 2 + y 2 y d x − x 2 + y 2 x d y
for some simple closed curve C that does not run through the origin?
If you come to the conclusion that there are infinitely many such I , enter 666.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
This is the right explanation for those of us who have taken a first course in complex calculus (+1); see the relevant facts here . But how are we going to explain this to the majority of our young friends at Brilliant who have not taken such a course yet (assuming that they have studied multivariate calculus through Stokes' Theorem)?
Small correction: I is negative 2 π times the winding number.
Log in to reply
Thanks for spotting the typo...
Given the abilities of our friends, it is odd that assuming a knowledge of Stokes' Theorem is acceptable, while assuming knowledge of Cauchy's Theorem is not. I learnt both in the same year when I was a student, many years ago. I do recommend learning some Complex Analysis to all serious analysts; it gives a new insight into many of the integration problems that this website produces, for example.
Anyway, to look at this problem without Complex Analysis...
If C is a curve in the plane, we can define I C = ∫ C ( x 2 + y 2 y d x − x 2 + y 2 x d y ) = ∮ C ^ F ⋅ d s where F is the function F ( x , y , z ) = ( x 2 + y 2 y , − x 2 + y 2 x , 0 ) and C ^ is the embedding of the 2 -dimensional curve C into R 3 achieved by putting C into the z = 0 plane.
Since ∇ × F = 0 away from the z -axis, we deduce that I C 1 − I C 2 = ∮ C ^ 1 F ⋅ d s − ∮ C ^ 2 F ⋅ d s = 0 for any two simple planar closed curves, provided that C 2 can be derived from C 1 by a homotopy in R 2 \ { ( 0 , 0 ) } . This means that one curve can be continuously deformed to the other, without passing through the point ( 0 , 0 ) .
For easy examples this can be seen by drawing an extra line, in that ∮ C ^ 2 F ⋅ d s − ∮ C ^ 1 F ⋅ d s = ∫ ∫ S ∇ × F ⋅ d S = 0 when it is possible to define (basically) C ^ 2 − C ^ 1 as the boundary of the region S between them (the actual boundary is C ^ 2 − C ^ 1 , plus the straight line segment in both directions), in which case the above formula is simply an application of Stokes' Theorem:
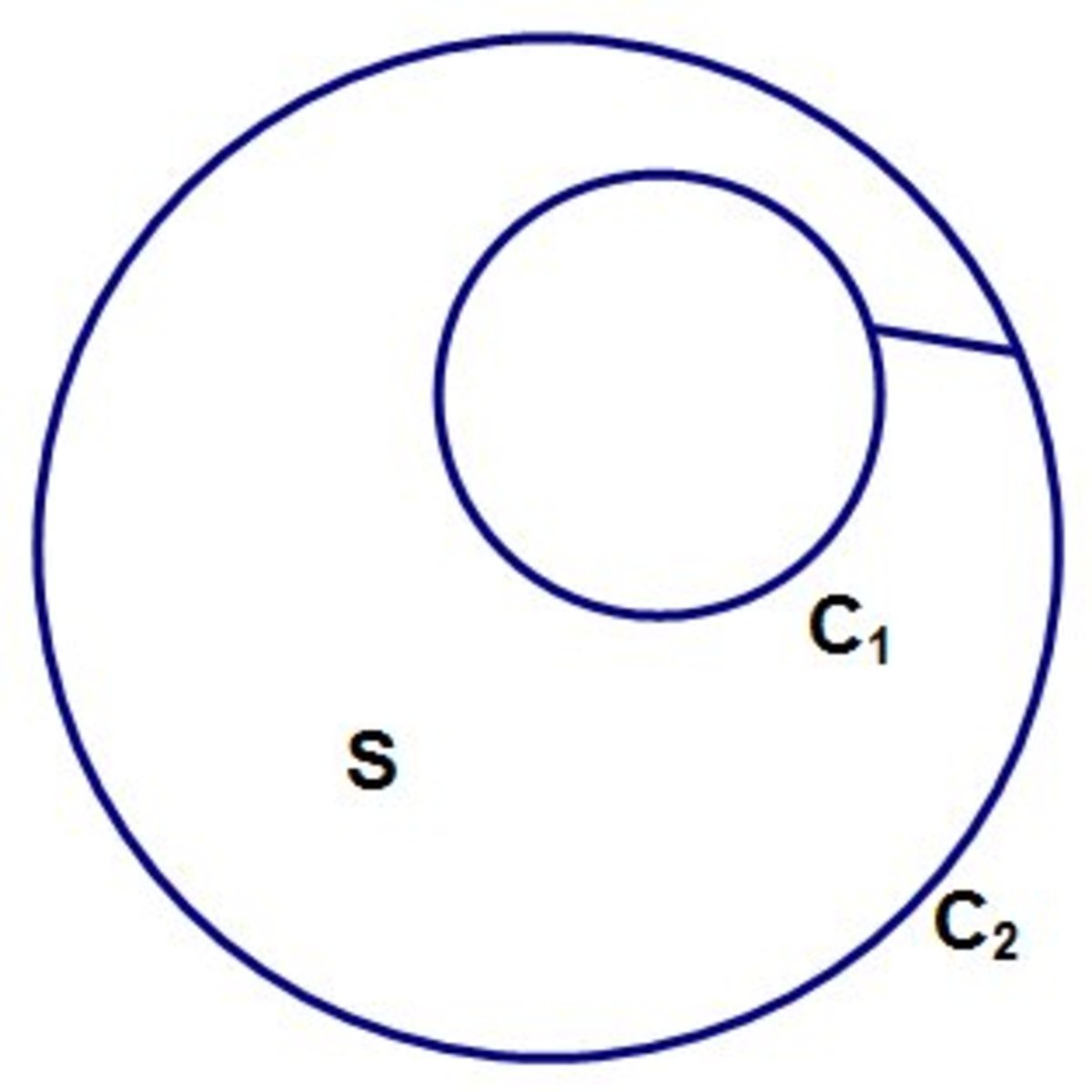
The details which are necessary to go between the easy and the general cases are substantial, and I will leave it to you to present them!
Given this result, however, it is clear that all simple closed curves C which do not contain 0 are homotopic to each other, and so have the same value of I C . Similarly, the simple closed curves which do have 0 in their interior are split into two groups, depending on whether the curve goes around 0 clockwise or counter-clockwise. Any two curves in the same group are homotopic, and so have the same value of I C .
Thus there are three classes of simple closed curves: ones that miss 0 , ones that encircle 0 clockwise, and ones that encircle 0 counter-clockwise. It simply takes working out the integral for an easy representative (a circle) of each class to discover that the corresponding values of I C are 0 , 2 π and − 2 π .
Log in to reply
Thank you for this very detailed analysis... I trust that it will help some of our "young friends".
At this stage, I avoid talking about homotopy. Instead, I argue as follows. (I always spend a whole hour on this important example in my classes.).
To make sure that we don't have to deal with too many issues at once, let's assume our students have studied Green's Theorem well and they know how to orient the boundary of their region in the case of "holes" (in the case of one hole, I usually explain this issue by cutting the region into two simply connected regions with a cut "through the hole").
Let's say we have two non-intersecting curves C 1 and C 2 with the origin being enclosed by both. Applying Green's Theorem to the region between them, we see that the counterclockwise circulation around C 1 plus the clockwise circulation around C 2 is zero, so that the two counterclockwise circulations are equal. The rest then follows trivially: We have a common circulation for all curves with winding number 1, the opposite circulation for those with winding number -1, and circulation 0 in the case of winding number 0 by Green's Theorem.
Log in to reply
@Otto Bretscher – The two non-intersecting curves case is basically the one I described, handling the nonzero and zero winding number cases according as 0 in either inside C 1 or outside C 2 .
If we are going to handle the other simple case, we need to consider curves C 1 and C 2 which intersect (like two Venn diagram circles), with 0 either in the intersection region or else in the complement of the union region. A different, but similar, argument shows that I C 1 = I C 2 in this case as well.
The problem, if we are not going to mention homotopy, is how to move from these easy pictures to the general result. One approach is to turn each curve into a mesh. Imagine covering the plane with narrow-gauge chicken-wire. Every loop integral can be seen as a sum of loop integrals over the many loops formed by the intersection of the chicken-wire with the original loop. If we now consider two different loops, then (provided the gauge of the chicken-wire is small enough) the mesh loops forming the two big loops are either disjoint or else intersect trivially, and so the "easy" arguments can be used to justify the general result.
If we are being picky, then this technique quietly ignores a large number of technical details about the nature of the types of curves we are interested in. We can get the "big picture" without the details, but only a discussion of homotopy can really handle the problem fully.
Log in to reply
@Mark Hennings – I handle the case of two intersecting curves C 1 , C 2 (with the origin being enclosed by both) as follows: Consider a third curve C 3 that intersects neither, perhaps a sufficiently large circle... and you are done: I C 1 = I C 3 = I C 2 if all have the same orientation.
What do you mean by "the general result"? I'm not quite seeing what we are trying to prove.
Log in to reply
@Otto Bretscher – Two simple closed curves could intersect each other many times, not just twice; how can we be sure that the two simple cases are enough to deal with all of the possibilities? We can deal with this by a mesh argument provided that there are only finitely many intersections, which ensures that two mesh subcontours, one from each contour, will intersect at most twice (for a small enough mesh). We basically need to ensure thst there is no accumulation point in the set of intersections - the simple cases would not handle really pathological examples.
There are still special cases to consider. What if two curves coincide for a while? Again, this can only happen a finite number of times for us to be able to cope.
I am certainly not setting this out precisely - that is what textbooks are for - but am highlighting the issues that exist between the simple and the general.
Some form of "nice" differentiability of the contours is enough to exclude such exotica, or else to ensure that problem spots only occur finitely often, and a certain degree of differentiability is needed to be able to define the contour integrals, anyway.
Log in to reply
@Mark Hennings – Can't we avoid all this by considering a third curve that does not intersect either? See my last post. Maybe you are overthinking this?!
Log in to reply
@Otto Bretscher – Somewhere along the line you have to address these issues. With care, your argument will handle the nonzero winding number case, yes. But you are then consigning the problems I am highlighting to Stokes' Theorem. Any proof of this result has to handle these problems, and most textbook proofs do no go into the details of the levels of complication possible. ideas like homotopy are what are needed to enable the simple cases to deal with the more general.
Log in to reply
@Mark Hennings – I don't think we need to deal with this messy issue of intersecting curves if we have a sufficiently robust version of Green's Theorem (a big "if" though).
The way things are done in the US, we usually don't prove all the technical details in a first course. If the students get far enough, they will eventually see the short and neat proof of Stokes' Theorem on manifolds... by then the definitions and notations are so strong that there is almost nothing left to prove, as in Spivak's beautiful booklet "Calculus on Manifolds."
Log in to reply
@Otto Bretscher – Stokes' Theorem on manifolds is, as you say, beautiful and elegant. It also contains all the nitty-gritty that I have been referring to (not so much in the proof itself as in the setting-up exercises which define the various elements of the result). The whole business of local charts corresponds to finding a suitable mesh for our problem.
Throwing such a big gun at the problem is requiring about the same level of sophistication (perhaps more) as invoking winding numbers, though.
As you say, a hand-waving argument, assuming that all curves are moderately well-behaved, satisfies most students to begin with.
The integral I is just − 2 π times the winding number of the oriented closed curve C about the origin 0 . In complex number terms, I is the contour integral I = − i 1 ∫ C z d z , making the obvious identification between the Argand diagram and the plane via the formula z = x + i y .
An oriented simple closed curve will either have 0 in its interior (and hence will have winding number ± 1 according as it goes around the point 0 in a counter-clockwise or clockwise direction) or else will not have 0 in its interior (and hence will have winding number 0 ). Thus the only possible values of I are ± 2 π and 0 . The answer is 3 .