Hey ant, I just want a word for you: the word is stop!
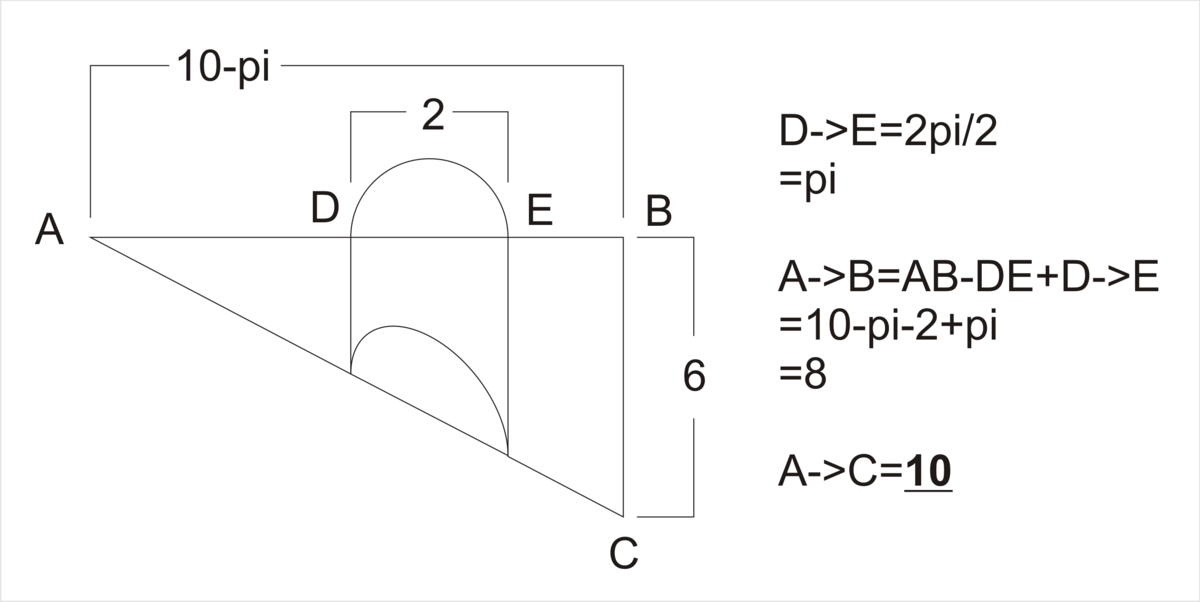
 In the figure shown above
is a right triangle with
,
and
. There is a semi-cylinder with radius
and its axis is perpendicular to
. That little ant in point
must scape to point
soon! What is the length of shortest way for him to going to his nest in point
?
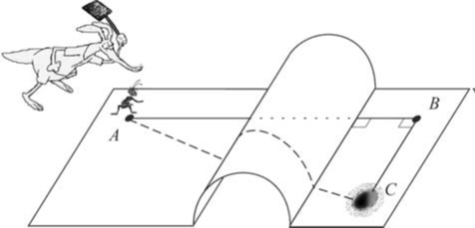
In the figure shown above
is a right triangle with
,
and
. There is a semi-cylinder with radius
and its axis is perpendicular to
. That little ant in point
must scape to point
soon! What is the length of shortest way for him to going to his nest in point
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.