Let's have some trivialities!
In Δ A B C , B C is the perpendicular (internal) bisector of the line segment joining the circumcircle and incenter . Find ∠ B A C in degrees.
This problem is part of my set: Geometry
The answer is 108.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
Great synthetic approach with simple angle chasing! Wasn't expecting it. Thanks for sharing :)
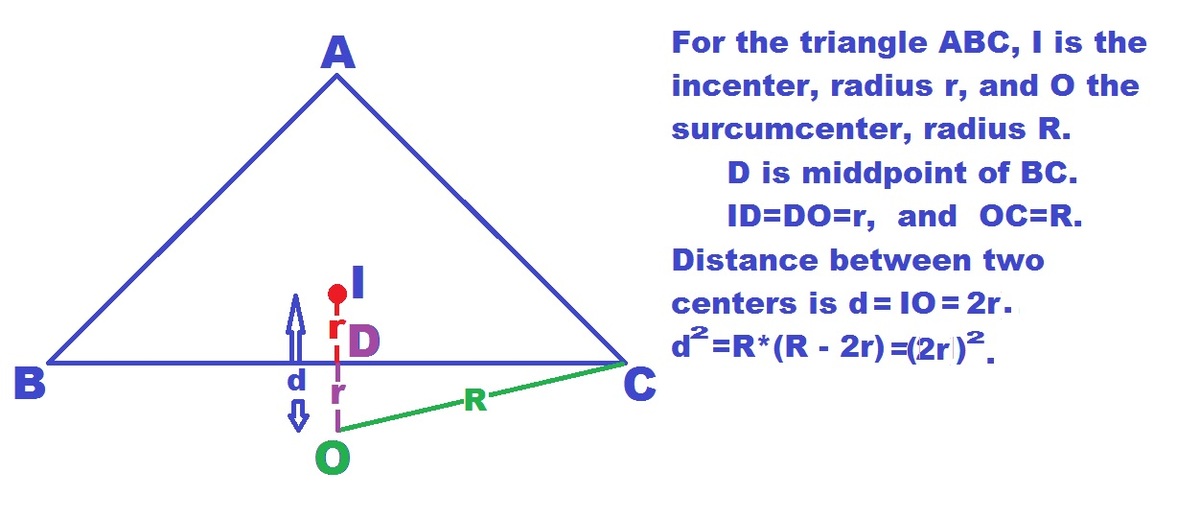 Refer to the sketch. I is always within the triangle. But BC is INTERNAL perpendicular
bisector of IO.
∴
(1) O is outside, (2) ID=DO=r
.
⟹
(
1
)
∠
A
>
9
0
o
,
(
2
)
d
=
2
r
.
Refer to the sketch. I is always within the triangle. But BC is INTERNAL perpendicular
bisector of IO.
∴
(1) O is outside, (2) ID=DO=r
.
⟹
(
1
)
∠
A
>
9
0
o
,
(
2
)
d
=
2
r
.
link text
d
2
=
R
∗
(
R
−
2
r
)
=
(
2
r
)
2
.
⟹
4
∗
(
R
r
)
2
+
2
∗
R
r
−
1
=
0
.
S
i
n
c
e
∠
A
>
9
0
o
,
w
e
t
a
k
e
−
t
i
v
e
s
i
g
n
a
n
d
g
e
t
R
r
=
−
4
1
+
5
=
C
o
s
E
O
C
.
∴
∠
E
O
C
=
1
0
8
o
.
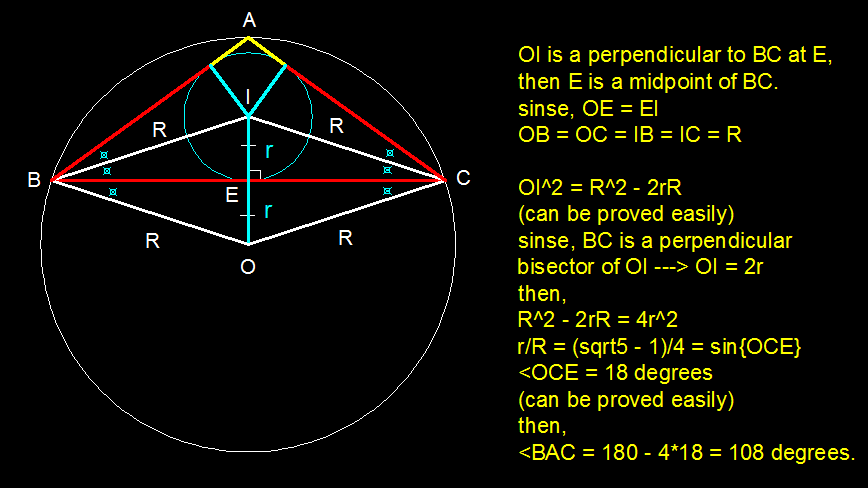
BC makes angle 2*EOC at the circumcenter while angle A at the circumference,
∴
∠
A
=
2
1
∗
2
E
O
C
⟹
∠
A
=
1
0
8
.
How is it that the ratio of lengths is negative?
Log in to reply
These are directed line segments, meaning that the signage tells you which direction the line is pointing in. IE ∣ B C ∣ = − ∣ C B ∣ .
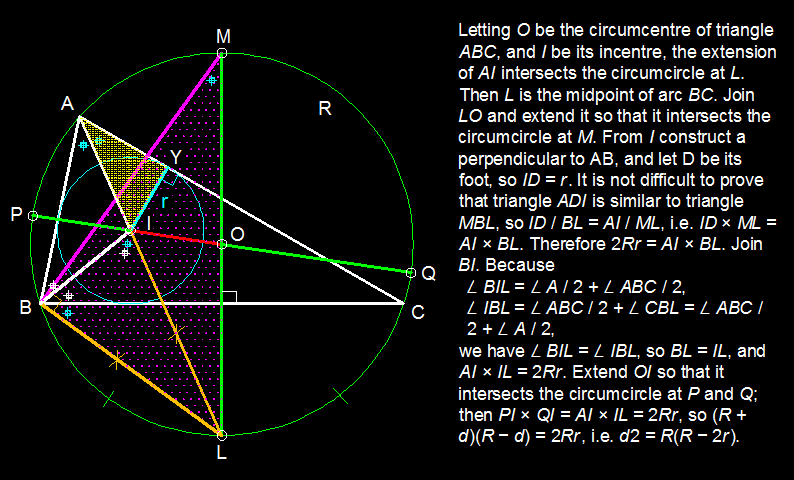
Euler's theorem in geometry
From Wikipedia, the free encyclopedia
[https://en.wikipedia.org/wiki/Euler'stheoremin_geometry)
I think we can improve your solution: After you've proved that B I C O is a rhombus, ∠ B I C = ∠ B O C . But ∠ B I C = 9 0 ∘ + 2 ∠ B A C , and ∠ B O C = 2 ( 1 8 0 ∘ − ∠ B A C ) , we have this equation:
2 ∠ B A C + 9 0 ∘ = 2 ( 1 8 0 ∘ − ∠ B A C ) ⇒ ∠ B A C = 1 0 8 ∘ .
Log in to reply
Hadn't thought of it that way. Thanks for sharing!
Yeah that is faster ^^
Exactly! But, you could've either added some wiki links, an outline or a small comment about the proof for I O 2 = R 2 − 2 r R
Log in to reply
Euler's theorem in geometry
[https://en.wikipedia.org/wiki/Euler's theorem in_geometry]
Log in to reply
Euler's theorem Here's the link.
Log in to reply
@A Former Brilliant Member – Thanks, appreciate your assistance.
Let O and I be perpendicular to BC meet BC at D.So in triangle IOD , angle IBD=B/2,ID=r(inradius),BD=a/2(OD perpendicular bisector).So r= 2 a tan( 2 B ).Also we know r=(s-b)tan( 2 B ).Equating we get b=c. Now O is outside and I inside the triangle.angle OBD=angleIOD(since ID=OD given)=B/2.And angleBOD=angleBOA=2C.Alao C=B.Now angle chasing in triangle OBD yields B=B=36.Hence A=108.
Let ∠ B A C = x .
For B C to be the perpendicular biscetor of O I , it follows that the midpoint of O I must be the midpoint of B C as O is on the perpendicular biscetor of B C .
By symettry, △ B I C is similar to △ B O C by reflecting across B C .
∠ O B C = ∠ I B C = 2 ∠ B because I is on the bisector of ∠ B . We have a similar result for ∠ O C B .
∠ B O C = 1 8 0 ∘ − 2 ∠ B − 2 ∠ C = 1 8 0 ∘ − ( 2 ∠ B + ∠ C ) = 1 8 0 ∘ − 2 1 8 0 ∘ − ∠ A ) = 9 0 ∘ + 2 x
Let D be a point on the circumcircle of △ A B C on the opposite side of B C to A .
∠ B D C = 2 9 0 ∘ + 2 x = 4 5 ∘ + 4 x because angle at circumference is half angle at center.
A B D C is cyclic gives:
∠ B A C + ∠ B D C = 1 8 0 ∘ ⇒ x + 4 5 ∘ + 4 x = 1 8 0 ∘ ⇒ 4 5 x = 1 3 5 ∘
x = 1 0 8 ∘