Incenters Are Important
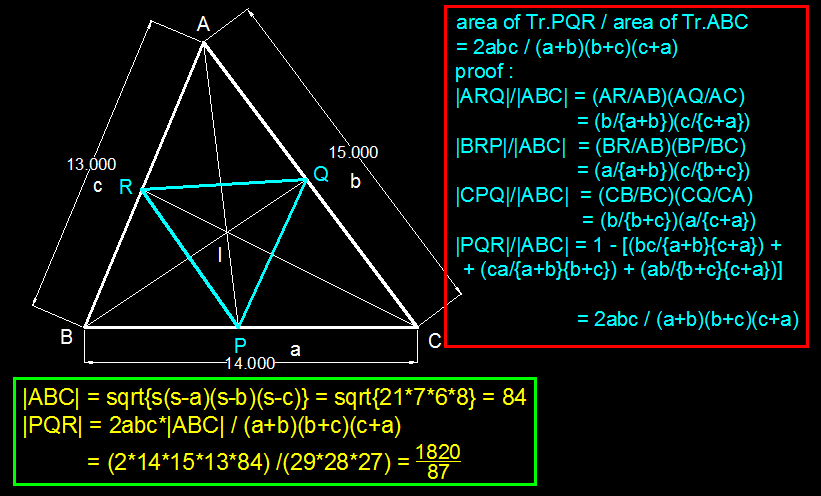
The internal bisectors of the angles of the Δ A B C meet the sides B C , C A and A B at the points P , Q and R respectively. If A B = 1 3 , B C = 1 4 , C A = 1 5 , find the area of △ P Q R .
If this area can be expressed as N M , where M and N are coprime positive integers, find M + N .
The answer is 1907.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Akshay Yadav Nice solution.....but it would be great if we could generalise it for all triangles with sides a,b,c.
Log in to reply
Mohit here is the generalized formula (I won't be providing its proof as its very long)-
a r ( △ P Q R ) = ( a + b ) ( b + c ) ( c + a ) 2 a b c × a r ( △ A B C )
Where a , b and c are sides of △ A B C .
Log in to reply
Ya correct!!!!!!!!absolutely......i also derived the same :)
is there any link on google from where i can get the proof of this
Log in to reply
@Deepansh Jindal – The proof of the formula comes from what I did in the solution, just try to generalize it.
Log in to reply
@Akshay Yadav – i am not getting it it would be better if you provide a particular solution of the derivation
Log in to reply
@Deepansh Jindal – I will give you a short insight of the proof-
Consider the same triangle as I used in the generalized formula and my solution. We know that angle bisectors divide the side on which fall into the same ratio of other two sides (see solution).
So,
A P = a + b b c , P B = a + b a c , B Q = b + c a c , Q C = b + c a b , C R = a + c a b and R A = a + c b c .
Also,
sin ∠ A = b c 2 × a r ( △ A B C ), sin ∠ B = c a 2 × a r ( △ A B C ) and sin ∠ C = a b 2 × a r ( △ A B C ).
Now using this information to calculate area of △ A P R , △ B Q P and △ C R Q .
a r ( △ A P R ) = ( a + b ) ( b + c ) b c × a r ( △ A B C )
a r ( △ B Q P ) = ( b + c ) ( a + b ) c a × a r ( △ A B C )
a r ( △ C R Q ) = ( c + a ) ( b + c ) a b × a r ( △ A B C )
Now I leave the rest to you, you just need to subtract these areas with the area of △ A B C (as done in the solution), after lots of algebra and simplification you will get the answer.
Log in to reply
@Akshay Yadav – Proof is not at all long if you try using vectors.
Log in to reply
@Manish Maharaj – I am using simple geometry here! :)
@Deepansh Jindal – @Deepansh Jindal I have tried my best to explain the proof to you.
It was foolish of me apply cosine rule and then calculating sine of each angle by indentity, isn't it? I should have rather calculated that directly.
@ahmad saad which software do you use for these geometrical diagrams?
Log in to reply
AutoCAD software.
It's used across a wide range of industries, by architects, project managers, engineers, graphic designers, and other professionals.
You can get it from Web sites.
AutoCAD is licensed, for free, to qualifying students and teachers, with a 18-month renewable license available.
Good and simple question. I enjoyed it thoroughly!
We know that angle bisectors divide the side on which fall into the same ratio of other two sides,
Here x a = y b .
Using the following theorem we get,
A P = 2 9 1 9 5 cm, P B = 2 9 1 8 2 cm, B Q = 2 1 3 cm, Q C = 2 1 5 cm, C R = 9 7 0 cm and R A = 9 6 5 cm .
Also by cosine rule,
cos ∠ C A B = 6 5 3 3 , cos ∠ A B C = 1 3 5 and cos ∠ B C A = 5 3 .
Hence we can find the sine of each angle.
sin ∠ C A B = 6 5 5 6 , sin ∠ A B C = 1 3 1 2 and sin ∠ B C A = 5 4 .
Now,
a r ( △ A P R ) = 2 1 × 2 9 1 9 5 × 9 6 5 × 6 5 5 6 = 8 7 1 8 2 0 cm²
a r ( △ B Q P ) = 2 1 × 2 9 1 8 2 × 2 1 3 × 1 3 1 2 = 2 9 5 4 6 cm²
a r ( △ C R Q ) = 2 1 × 2 1 5 × 9 7 0 × 5 4 = 3 7 0 cm²
So,
a r ( △ P Q R ) = a r ( △ A B C ) − a r ( △ A P R ) − a r ( △ B P Q ) − a r ( △ C Q R )
a r ( △ P Q R ) = 8 4 − 8 7 1 8 2 0 − 2 9 5 4 6 − 3 7 0
a r ( △ P Q R ) = 8 7 1 8 2 0 cm².