Let's try with Electrostatics

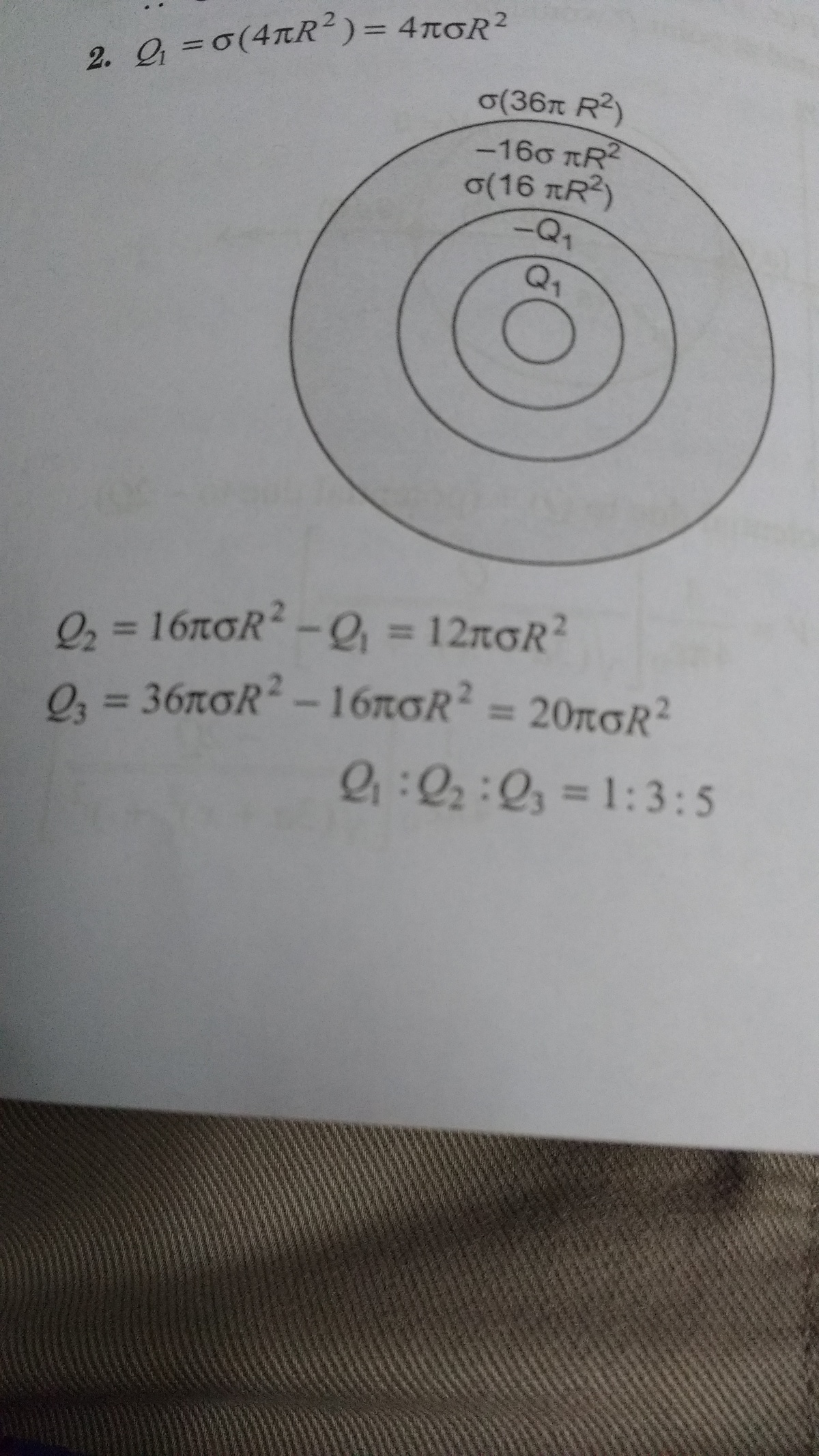
Similar to Md Zuhair's approach but explained a bit differently.

---

Using Gauss's Law, we have

$\Phi_E = \oint_S {\displaystyle \overrightarrow{\mathbf {E}} \cdot \mathrm {d} \overrightarrow{\mathbf {S}} } = \frac{Q}{\varepsilon_0}$

where

• $\Phi_E$ denotes the total electric flux present on a closed surface $S$ enclosing a volume $V$ .
• $Q$ is the total charge enclosed within $V$ .
• $\mathbf {E}$ is the electric field.
• $\varepsilon_0$ is the vacuum permittivity constant $(\varepsilon_0 = 8.85 \times 10^{-12} \text{ F⋅m}^{-1} )$ .

So for our three spherical shells, the respective total charges are

• $Q_1$ for shell with radius $R$ .
• $Q_1 + Q_2$ for shell with radius $2R$ .
• $Q_1 + Q_2 + Q_3$ for shell with radius $3R$ .

Since the respective surface charge densities are equal, we have

$\dfrac{Q_1}{4 \pi R^2} = \dfrac{Q_1 + Q_2}{4 \pi {(2R)}^2} = \dfrac{Q_1 + Q_2 + Q_3}{4 \pi {(3R)}^2}$

Solving this system of equalities, we get

$Q_1 = \dfrac{Q_2}{3} = \dfrac{Q_3}{5}$

Thus, $Q_1 : Q_2 : Q_3 = 1 : 3 : 5 \implies a+b+c = \boxed{9}$ .

---

Generalization:

For shells with radii $m$ , $n$ and $k$ (from the innermost being $m$ and outermost being $k$ ), we have

$\dfrac{Q_1}{4 \pi m^2} = \dfrac{Q_1 + Q_2}{4 \pi n^2} = \dfrac{Q_1 + Q_2 + Q_3}{4 \pi k^2}$

Solving this system of equalities, we get

$Q_1 = \dfrac{Q_2 \ m^2}{n^2 - m^2} = \dfrac{Q_3 \ m^2}{k^2 - n^2}$

Thus, $Q_1 : Q_2 : Q_3 = m^2 : (n^2 - m^2) : (k^2 - n^2)$ .