Levitating Pentagon
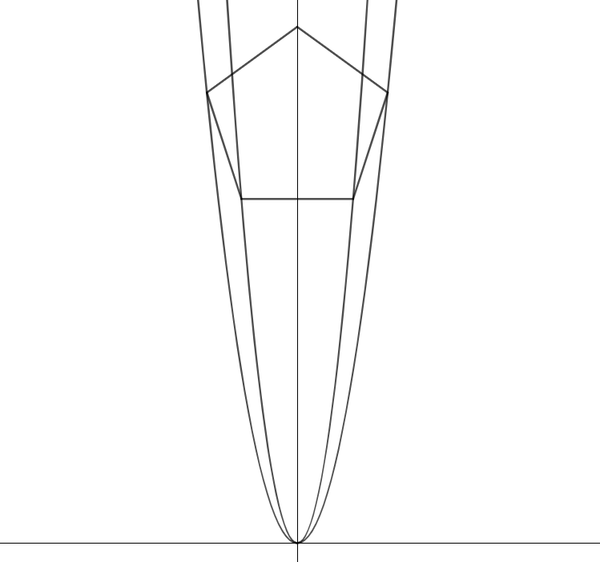
In the Cartesian plane, the regular pentagon is formed by the vertical axis and two graphs y = x 2 and y = 2 x 2 , where two pairs of common vertices are symmetric about the vertical axis.
If the area of the pentagon can be expressed as A B + C D where A , B , C , and D are positive integers and D is square-free, input A + B + C + D as your answer.
The answer is 133.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
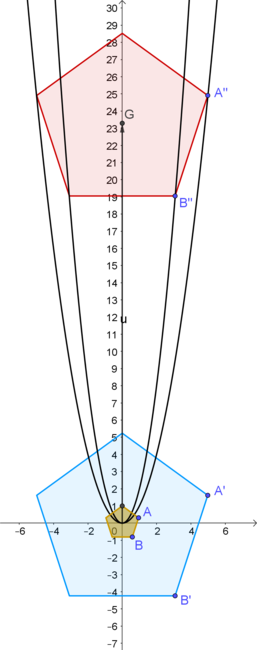 In the figure, the small yellow regular pentagon has circumradius 1, its center is at the origin and the y-axis is an axis of symmetry.
A
and
B
are two of its vertices. As we can see
here
, the coordinate of these vertices are
x
A
=
4
1
0
+
2
5
y
A
=
4
5
−
1
x
B
=
4
1
0
−
2
5
y
B
=
4
5
+
1
If we enlarge the pentagon to get the blue one with circumradius
R
, the corresponding vertices are
A
′
(
R
x
A
,
R
y
A
)
and
B
′
(
R
x
B
,
R
y
B
)
“Levitating” this pentagon to the desired place by a vector
(
0
c
)
, the vertices become
A
′
′
(
R
x
A
,
R
y
A
+
c
)
and
B
′
′
(
R
x
B
,
R
y
B
+
c
)
for some positive real number
c
.
In the figure, the small yellow regular pentagon has circumradius 1, its center is at the origin and the y-axis is an axis of symmetry.
A
and
B
are two of its vertices. As we can see
here
, the coordinate of these vertices are
x
A
=
4
1
0
+
2
5
y
A
=
4
5
−
1
x
B
=
4
1
0
−
2
5
y
B
=
4
5
+
1
If we enlarge the pentagon to get the blue one with circumradius
R
, the corresponding vertices are
A
′
(
R
x
A
,
R
y
A
)
and
B
′
(
R
x
B
,
R
y
B
)
“Levitating” this pentagon to the desired place by a vector
(
0
c
)
, the vertices become
A
′
′
(
R
x
A
,
R
y
A
+
c
)
and
B
′
′
(
R
x
B
,
R
y
B
+
c
)
for some positive real number
c
.
Since
A
′
′
and
B
′
′
belong to the parabolas
y
=
x
2
and
y
=
2
x
2
respectively, we have the following system of equations
R
y
A
+
c
=
(
R
x
A
)
2
R
y
B
+
c
=
2
(
R
x
B
)
2
Combining we get
R
(
y
A
−
y
B
)
=
R
2
[
(
x
A
)
2
−
2
(
x
B
)
2
]
⇒
R
=
(
x
A
)
2
−
2
(
x
B
)
2
y
A
−
y
B
Plugging the corresponding values we find
R
=
3
+
5
Using the
formula for the area
of a regular pentagon with circumradius
R
, we have
A
=
4
5
R
2
2
5
+
5
=
4
5
(
3
+
5
)
2
2
5
+
5
=
…
=
5
8
5
+
3
8
5
For the answer,
a
=
5
,
b
=
8
5
,
c
=
3
8
,
d
=
5
, thus,
a
+
b
+
c
+
d
=
1
3
3
Gahhhhhhhh, using Cartesian geometry, I've found the two coordinates of the regular polygon in the first quadrant to be ( a , 2 a 2 ) , ( b , b 2 ) , where
And I got the area denoted as
c
in WolframAlpha. But it doesn't let me simplify to a simple radical... Mathematica couldn't help either!!!

Log in to reply
That's weird. The values match mine, by the way. I've found Wolfram|Alpha can sometimes struggle with what should be relatively simple calculations for it. Sometimes weird things like just changing the order of the terms, or relabelling variables seems to help, but it would be nice to know exactly why it stops working. Have you found this issue?
(by the way, your link to Alpha doesn't match the screenshot)
Log in to reply
found the issue? Well yeah, but i don't know how to resolve it... yet
Log in to reply
@Pi Han Goh – I mean more in general. It comes up a lot for me with Alpha; the most annoying thing is when I use Alpha's own output as an input and it's not recognised.
Log in to reply
@Chris Lewis – I'm still a newbie in Mathematica so I don't know the answer....

](../../brioche/uploads/MTj3IwB5IJ-image-15.png?width=1200)
Note that the curve y = x 2 is red and y = 2 x 2 is blue. Let A = ( u , 2 u 2 ) and B = ( v , v 2 ) . Then the side length of the regular pentagon is 2 u . Then we have:
v = u + 2 u sin 1 8 ∘ = u + 2 u ( 4 5 − 1 ) = ( 2 1 + 5 ) u = φ u
where φ denotes the golden ratio . And:
v 2 = 2 u 2 + 2 u cos 1 8 ∘ = 2 u 2 + 2 u 8 5 + 5 = 2 u 2 + u 5 φ
Therefore,
φ 2 u 2 ( φ 2 − 2 ) u ( φ + 1 − 2 ) 2 u 2 φ 2 u 2 ⟹ u 2 = 2 u 2 + u 5 φ = 5 φ = 5 φ = 5 φ = 5 φ 3 Note that φ − 1 = φ 1
The area of regular pentagon:
A 5 g o n = 5 u 2 tan 5 4 ∘ = 5 5 φ 3 1 + 5 2 = 5 5 φ 3 5 5 + 1 + 1 = 5 5 φ 3 5 2 φ + 1 = 5 5 φ 3 5 φ 3 = 5 5 φ 9 = 5 5 ( 3 4 φ + 2 1 ) = 5 5 ⋅ 1 7 + 1 7 5 + 2 1 5 = 5 8 5 + 3 8 5 Note that φ n = F n φ + F n − 1 , where F n denotes the n th Fibonacci number.
Therefore A + B + C + D = 5 + 8 5 + 3 8 + 5 = 1 3 3 .