Lick Stick
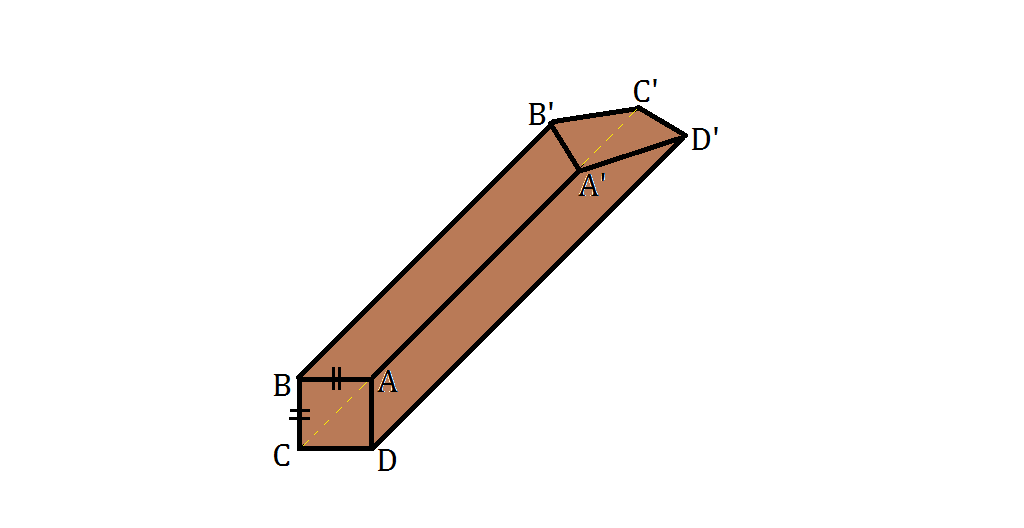
Charlie was aiming to launch the new chocolate bar products in the name of "Lick Stick". Originally, he designed it as a common cuboid shape, but due to unexpected manufacturing error, it resulted in a bizarre square-based polyhedron with quadrilateral faces. As shown above, A B C D is a square of 2 cm. length with varying heights of AA' = 11 cm.; BB' = 12 cm.; CC' = 14 cm.; DD' = 13 cm.
In desperation, he released the products out anyway to cut the loss, but to his surprise, all the Lick Sticks were sold out in popularity and, thus, became one of his top sales ever since.
What is the volume of each Lick Stick in c m . 3 ?
Note : Figure not drawn to scale.
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The face A'B'C'D' isn't a plane, since AA'+CC' = 24 is not the same as BB' + DD' = 26. Hence, there's ambiguity about what kind of a surface A'B'C'D' is. When a duplicate piece is joined with the original end-to-end as shown, the surfaces may not necessarily match as to make a solid long piece. Think of folding a square piece of paper along its diagonal somewhat, and then have a duplicate of it, turn it around, and try to match them.
One way to resolve this would be to make A'B'C'D' a ruled surface, i.e. every point on it has its distance from the other end expressed as follows
( A ′ ( 2 1 − x ) + C ′ ( 2 1 + x ) ) ( 2 1 − y ) + ( B ′ ( 2 1 − x ) + D ′ ( 2 1 + x ) ) ( 2 1 + y ) , where x , y are variables from − 2 1 to 2 1 .
Then the two faces will mesh perfectly.
Anoither way to fix the problem is to switch the lengths of CC' and DD', so that AA'+CC' = BB' + DD' = 25, and A'B'C'D' would be a planar face.
Log in to reply
Can't we connect AA' to another DD' and CC' to another BB', as shown in my solution?
Log in to reply
The original and the duplicate will match at points A', B', C', D', but what about the center of A'B'C'D'? The center may not actually be at (1/4)(A'+B'+C'+D') if A'B'C'D' is not a planar surface. See the problem?
Log in to reply
@Michael Mendrin – OK. Now it's changed as you've suggested. :)
As far as I can tell, ABD and CBD are coplanar, but the four points are not. I did a piece-wise double integral to solve, and ended up with 44 + 6.67 = 50.67.
But it looks like the numbers have been changed, presumably to make them coplanar
As shown above, if we join 2 Lick Sticks, it will result in a typical square-based cuboid. According to Cavalieri's principle, the overall cuboid's height = AA' + CC' = BB' + DD' = 11+14 = 12+13 = 25.
Hence, the volume of each Lick Stick equals to half of the cuboid: 2 1 × 2 × 2 × 2 5 = 5 0 .