Lift Weight
Pam normally weighs 6 0 k g , but one day she measured her weight in an elevator as 7 0 k g .
Can we say for sure whether the elevator was moving up or down at the moment she measured her weight?
The red arrows indicate the direction of motion.
Hint: Consider not just the velocity, but the acceleration of the elevator. Do velocity and acceleration always have the same direction?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Nice solution, +1 from me.
However I think your proof would be clearer if you replaced 'the elevator' with 'Pam' .
Arjen -- I agree with Peter (not that it probably means anything to you). Did you have a reason to use 'elevator' instead of 'Pam' ? In that same sentence you refer to the scale; the elevator is not on a scale - Pam is.
Log in to reply
Correct. I'll make the change.
Log in to reply
I continue to love your work. Not only does it have mathematical rigor, it is laid out neatly. You are the man.
At acceleration just like in a train you feel a force of artificial gravity pushing you back, with oil on the ground heavier ovjects will go to the back and lighter gasses and stuff will move to the front of the train(this is onlu during accelaration). When increasing speed going up, gravity is higher as it is working against pam weight that was stationary and now must be moved to reach acceleration in a other direction. The lift is working against her weight pushing her down+ the aditional force to move her around so it has to move her 10kg extra which is being translated into movement. At first pan is heavier, when pam reaches the same velocity/speed as the lift then her weight will become normal. So it is possible to become heavier. Its just during the acceleration. Nothing is said about pams velocity direction and that why precisly it is possible in some scenarios.
Log in to reply
Also acceleration = force over time(some form of constant force). If you gave 20kg push against something and 2 seconds later another one its accelerating. And then it will eventually reaches its max its just as children playing with a playground rad(rotating circle platform) they keep pushing accelerating the rotation speed, but it doesnt stay increasing the speed till its becoming a serious spinning sportscarwheel flinging all the kids of it and injuring them, it stops speeding eventually, this is due the particles(children) that were pushing it with speeded/mass (their hands) till the wheel reaches the same kind of acceleration speed as the children could. If something doesnt accelerate more it means it has reached same the power/speed of the things that kep pushing it. If you want to increase the speed more, it only will go faster when you have something that has a higher speed like putting the wheels of a motorcycle against that playground rad/rotating circle platform/(idk how to call it excuse me) it will radically increase the speed and become dangerous to stand on.
How does the velocity affect this question? And why is 'a' shown to be positive by virtue of m' being greater than m?
Log in to reply
Because even with the lift moving up, it could be decelerating or vice versa. They haven't given the direction of a.
The proposed solutions are no solutions, there is no such thing as an apparent mass in your equations, you are suggesting mass is created by a convulated way of misusing Newtown's laws. You are also not proving anything here. All the suggested answers are wrong, as the question is wrong, her weight did not measure 70 kg as mass is not equal to weight. The question should have read along the lines ".. Pam's weight is 70 x 9.81 N(ewton) ", the 9.81 m/s^2 the acceleration due to Earth's gravity. The suggested answer is also incorrect as both situations are certainly not the same, as in A Pam is increasing in potential energy and in B decreasing in potential energy.
Log in to reply
You are right that mass and weight are different concepts. When we say "her weight measured 70 kg", we mean that the scale was subjected to a normal force that normally would produced by a 70-kg object. In other words, F n = m ′ g , where m ′ is the "apparent mass" read off the scale.
A quick workaround is to say that "her weight measured 70 kgf (kilogram-force)", where 1 k g f : = 1 k g ⋅ g ≈ 9 . 8 1 N .
You bring up the concept of energy: it is true that in A Pam's potential energy is increasing, and in B her potential energy is decreasing. But that does not mean that the reading of the scale is the same. To do an energy analysis here, you should also account for the change in kinetic energy.
Log in to reply
Arjan, no, you are approaching this all wrong. The mass m remains the mass m, there is no m'. There could be an acceleration a' resulting in an extra force, resulting in a different reading of the scale.
At the instant the elevator is moving, it accelerated, resulting in a force which will be picked up by the scale as the force is also acting on the scale. The scale is just a measurement of how much difference in force is applied compared to the scale at "rest". You have to calibrated the scale so you can say "I weigh 70 kg" or better yet "I weigh 700 N(ewton)" (g taken to be 10 m/s^2)
Replying to your last statement, in your first answer you brought up a lot of equations, and ended with saying "...which we solve for to obtain the desired equation." You never expressed which was the correct one, which is clearly A. Now you are saying the situations are not the same, which is true. I brought up the potential energy to make clear the situations A and B are different as the proposed answer wrongly suggests that "Both situations A and B are possible" whatever that means.
We don't have to do any energy analysis for this problem, we don't even have to resort to equations, just a thought experiment : Suppose the elevator is in free fall (a = 9.8 m/s^2), how much force can Pam exert on the scale ? The scale should read zero Newton, everything inside the elevator is also in free fall and therefore weightless. Lets now suppose the elevator is accelerating in the opposite direction as in A with a = 9.8 m/s^2. What is the reading of the scale now ? It is a simple classical mechanical problem, nothing mysterious or deep and no apparent masses m'
Log in to reply
@W N – By "apparent mass" I don't mean anything profound; it simply refers to the reading of 70 kg on the scale.
The correct answer is "both A and B are possible": A when the lift is moving upward and speeding up, and B when the lift is moving downward and slowing down.
I agree that no energy-analysis is needed here. I only brought it up because you talked about potential energy.
As for the free-fall analogy: there are also two possible scenarios in which Pam would be weightless:
-
if the elevator is accelerating downward at rate g
-
if the elevator has been launched upward, and is currently still moving upward but decelerating at rate g (a projectile before it reaches its highest point)
Log in to reply
@Arjen Vreugdenhil – Your answer "The correct answer is "both A and B are possible": A when the lift is moving upward and speeding up, and B when the lift is moving downward and slowing down." is not the answer to the question. These are assumptions, the lift speeding up in A or slowing down in B.
The original question is strange : Pam normally weighs 60 kg but in an elevator, her weight measured 70 kg. What could have been happening at the instant her weight was measured?
Are we supposed to come up with wild scenario's (moving upward and speeding up, moving down ...) or do we apply the laws of Newton at that instant ? I am wondering what we are supposed to learn here ? Questions are rhetorical.
When we are standing in a lift, and it starts to move upward as in A, we can make the assumption the lift is accelerating as it starts to move, and is gaining in speed as we know from our own experiences up to the moment it reaches a certain constant velocity to make the journey pleasant. During this time or instant we feel an extra force, it is the acceleration of the lift acting on us, via the third law of Newton "For every action, there is an equal and opposite reaction." resulting in Pam not weighing 60 kg but 70 kg at that instant.
On your last comment about weightless on a projectile reaching its highest point, does not make any sense, launching upward (what is the acceleration here, or are we moving with a constant velocity) but decelerating at rate g ??? With the g of Earth's gravity also acting but transformed away somehow ?
Thaks for all the comments, but I really should concentrate on other things. I will read the replies for the coming week, but I am not going to reply, as it takes too much of my time.
Log in to reply
@W N – W N
During a launch, the projectile experiences upward acceleration. However, after the launch, while the projectile is still moving upward, it experiences acceleration due to gravity, which is downward. If the acceleration is in the opposite direction of the velocity, it describes the slowing down of an object; i.e. it is de celeration.
From inside the elevator, you cannot feel the difference between moving upward and slowing down, and moving downward and speeding up. In both cases, you experience downward acceleration.
As for Newton's Third Law: Note that the scale does not describe the upward force Pam feels, but rather the downward force the elevator experiences. This (normal-)force pair, of course, does satisfy Newton's Third Law; both forces are 70 kgf (about 700 N).
@Arjen Vreugdenhil – 'Elevator launched upward'. :-) Now THAT would be an elevator that I would NOT want to ever ride in. Talk about the elevator from he** !
Log in to reply
@Jesse Otis – W N talked about an elevator in free fall. That's just about as bad! :D
Log in to reply
@Arjen Vreugdenhil – Indeed, indeed; that would be the nightmare elevator! I well imagine that Einstein thought about that possibility in this thought experiments involving elevators.
Since A and B of question are unclear, A is correct solution, too.
Log in to reply
Fully agree. The question is not phrased well. When talking about weight in a question, I automatically assume arrows in a picture refer to acceleration and not movement. Therefore only A is correct, an upward acceleration creates more weight on a scale. The direction of movement is of course irrelevant. As in any frame of reference. BTW the elevator is also not moving straight up or down, because Earth rotation and the rotation around the sun ... you know where this is getting.
Log in to reply
Although the options do mention the diagram refers to the motion (and not the acceleration) of the elevators, I agree a little clarification wouldn't do any harm.
Also, I fail to see the impact of the rotation and revolution of the Earth around the Sun.
For the reading of the weighing machine to increase, the elevator must have an upward acceleration and it does not matter if it is at rest of going upwards or downwards.
If the elevator is going up with an increasing speed, the reading will increase
If the elevator is going down with decreasing speed, the reading will increase again.
Can you clarify what do you find unclear in the problem?
I think the question needs to be phrased a little clearer.
But why would the sum of the gravitational force and the normal force equal the subtraction and not the addition of m'g and mg? This is the only part I don't understand.
Log in to reply
The sum of the gravitational force and the normal force is a vector sum and as the gravitational force and normal force are opposite to each other, their sum equal the subtraction of m'g and mg. Suggested Reading - https://www.physicsclassroom.com/class/vectors/Lesson-3/Addition-of-Forces
Nevermind! Normal force is perpendicular to gravitational force.
Log in to reply
They are parallel, in opposite directions, in this case :)
I put C my reasoning is yes the scale will read a higher weight when she is traveling upwards, but if she was traveling downwards, the scale will read more when it slows to a stop.
nah this is dumb, this is not a real life situation. She might even have weighed 100lbs when the elevator going down stopped all of a sudden. That doesn't mean she believes she's 100lbs since the reading lasted 1 second. The only way for her to SEE it consistently and believe it's your weight is when she's going up. So this question is rather badly put.
Log in to reply
Her increase in apparent weight will only last 1 second for her reading going up as well, unless the elevator is accelerating for the ENTIRE upward trip (that would be fun but not super practical!). Otherwise, in normal elevators, she won't think she's heavier for the whole upward ride -- only for the brief 1-second acceleration upwards.
The increase in apparent weight is dependent upon the acceleration, which is momentary -- standing on a scale in an elevator going constant velocity up or down, however, will give the same reading of 60 kg.
First of all unit for weight is Newton, unit for mass is Kilogram. The question is wrong. Pam either weight 588.6 N or has a mass of 60Kg.
Arjen -- Do you know if there is an alternative method of corresponding with you? I would like to discuss physics and math with you. I know that Brilliant does not allow email addresses to be posted, so I'm out of luck there. Do you have a contact point at Trinity ? I could go to their website and contact you via that point.
Log in to reply
Search for me on Facebook. :)
The question needs a little correction, it should say 60 N and 70 N, instead of 60 kg and 70 kg, since mass remains constant everywhere.
Log in to reply
Nope......nothing wrong in it. The 'weight' measured by weighing machine does not remain constant everywhere.....
The actual mass is constant but the reading of the scale is not (depends on normal force).
Ah, I have made the mistake that going up was necessarily accelerating upward, and going down was partially falling.
Wrong, If the elevator were accelerating it wouldn't show stop on a measurement, it would go slightly up or down.
Log in to reply
I have no idea what you mean by that.
Log in to reply
Simple. If acceleration takes place.the reading would not remain constant. Period. In the description of the problem, there was no mention about reading on the scale changing "80kg during forst 3 seconds, then 70 for next 10 seconds" It said seventy kilograms. Tha's all. And knowing ONLY this result, I have my correctanswer ready. I've rght to assume that measurement is consistent and constant during some period of time. And this is guaranteed only if the lift was moving upward steadily. Abandon your mindset and loot at this from a perspective of person reading the text and only the text. You assume some extras which were not there.
Log in to reply
@Boguslaw Piskorz – If the lift were steadily moving upward (i.e. at a constant speed), the reading would be the same as when it is standing still: 60 kg.
But the reading is greater. This is only possible if there is upward acceleration, either because the elevator is going upward at an increasingly faster speed, or because it is going downward at a decreasing speed.
If the rate of acceleration is constant for a while, the reading is also constant for a while, even though the speed keeps changing.
I am challenging your "coorect solution". Namely, to make measurement with reading of 70kg, it takes some time to obtain the constant result. Since result was 70kg, it must have stay at the value for some time. Therefore, the answers "the elevator is going upward and speeding up
the elevator is going downward and slowing down" are wrong because in those circumstances, the value would be CHANGING with time. Therefore I am of opinion that the only correct answer is the elevator was steadily going UP! I don't give a damn about impressive formulas above. If it really was correct with speeding up of slowing down, you would obtain exact weight for infinitely SHORT time interval. I would not call this reading "70kg". For in the next time interval it would not be any more of the same value. Agree?
Log in to reply
You make the mistake of associating force with speed rather than with acceleration .
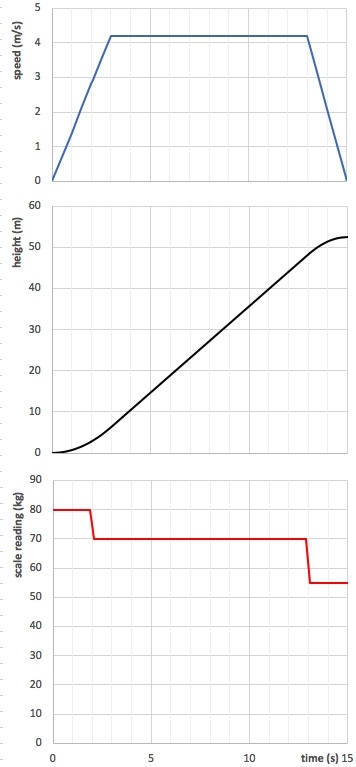
Let's take a more concrete example; the elevator moves upward and
-
first gradually speeds up from rest to 4.2 m/s in the first three seconds,
-
next keeps a speed of 4.2 m/s in the next ten seconds,
-
then gradually slows down to rest in the last two seconds.
In the case of a 70-kg person the reading of the scale will be 80 kg during the first three seconds, 70 kg during the next ten seconds, and 55 kg during the last two seconds.
The elevator could be accelerating while moving up, or decelerating while moving down.
Decelerating while going down is still an acceleration in the upward direction... the correct answer should be at the moment the measurement was taken there was an upward force applied
Log in to reply
Yeah, but I think my phrasing is still correct... after all, the upward force causes the elevator to literally decelerate
The correct answer is that the motion could be upwards, or downwards, or technically sideways. It's the acceleration that causes the change in force, but that acceleration is independent of the motion of the elevator at the time.
Log in to reply
Coming back to it, I realized my response was unclear.
Nader Hassan, I'm saying your response doesn't answer the question. Does the acceleration tell you what direction the elevator is moving? No.
Let's ask Pam. She'll say the elevator is going up because she has the reasonable expectation that acceleration, and hence her perception of up or down, is constant. If she thought she was a physics problem, someone should have told her before she got in the elevator. Poor thing. In any case, real world, the elevator - going either up or down - would be slowing. Stand in an elevator and pretend you're Pam. If it's not slowing both of you are in trouble. This is sort of a trick problem, or as Donald would say, rigged.
When you are using the elevator every time you can feel both upward and downward force independent on where you want to go. Because in any case you need to start motion with acceleration and then stop stop with deceleration. You need to specify not only a direction of elevator motion but also when measurement was done at the start or at the end.
Basically because she accelerates that means there will be force pushing her to the floor when the elevator goes up. But when the elevator slows down going down, she will not instantly slow down so she will feel a force. Hence, that will make her weigh more.
when the elevator was moving upwards all of her mass compressed the pad which made it go from 60 to 70 and if it were to go down it would made her light weight
If the elevator is moving smoothly upwards or downwards, her weight should register as 60. If the elevator is accelerating, that would alter her apparent weight, and in either case, moving up or down, the acceleration is necessarily upwards.
The answers ignore acceleration; the key is to realize that that instantaneous acceleration can occur during upwards or downwards motion of the elevator.
Yes exactly right!
Based on the way the answers were worded, I disagree with the "correct" answer. "Was moving up" or "was moving down" does not say anything about acceleration or deceleration.
Log in to reply
That's the whole point of the question though, you have to deduce that the elevator is accelerating in an upward direction from the fact that the scale shows 70kg whilst her mass is given as 60kg. You then have to realise that an upward acceleration is possible whichever direction the elevator is moving in. Incidentally it could also occur when the elevator has a velocity of zero. If we are getting really nit-picky we should really specify what we mean by upward and downward and we should also note that kg is a unit of mass not weight but, most domestic scales do in effect measure weight and display it in kg (assuming that you are not in actual fact weighing yourself in a lift as Pam has done)
Mass doesn't change.... It's constant.
What changes is our Weight(Newton)....which is related to gravity. In science, Weight is mass(constant) x acceleration due to gravity (9.8m/s2).
Now, gravity increases at the pole and decreases at the equator. why? Because of the distance between the Mass of the earth and our Body with respect to the radius.
I'm confident that as the elevator goes down and towards the center of the earth, the gravity decrease, the weight reduces and therefore your weight which should be 60kg x 9.8ms/2 reduces to maybe 60kg x 9.4m/s2 .... Due to the downward force, the result will be different.
And as the elevator moves up, the gravity increases from 9.8 to like 10.0m/s2....
so in elevator A which is going up, it will be 60N while the one going down will be 70N making you think the weight had increased which it hasn't... the mass is constant but the Gravity changed with depth!
Log in to reply
The weight change due to change in gravity is minimal, especially in what we could reasonably expect the path of the elevator to be. The correct line is that the acceleration of the elevator has changed.
I'm confident that you're misinterpreting something... Because gravitational attraction is inversely proportional to the square of the distance, so the "g" would increase towards the center of the earth, and decrease as you move away. :-B
Poor question - the answers say nothing about acceleration / deceleration. Therefore A is the correct answer - Brilliant !
Log in to reply
A lot of these puzzles are based on making rational assumptions about unprovided information. C is the BEST answer.
Log in to reply
C is the only answer, not the best answer. A and B are definitive statements that you know the elevator was either moving up or down, and both are incorrect, since it can't be determined from the data given.
The fact that the answers don't mention acceleration is the reason that C is the correct choice. Acceleration upwards would account for her weighing more, and that acceleration can occur regardless of the elevator's motion.
Only case A is possible because the observed weight has increased from normal weight. In case of B the pseudo force would be applied in opposite direction as that of gravitational force hence the observed weight should be less than normal weight in case of B. Hence only A is possible but why answer is both are possible.
Log in to reply
What matters is acceleration/deceleration not direction of movement. If the elevator is moving down and it starts to slow down, you will experience an apparent increase in weight until it stops.
1 chose C because i thought that its possible that the person gained weight. Cuz it says one day you know...
Upwards acceleration could indicate A) the elevator is moving upwards, and speeding up, or B) the elevator is moving downwards, and slowing down. Make sure you don't confuse motion in a direction with acceleration in that direction.
yeah i think that too! why isn't this correct?
Log in to reply
Because when you are going down in an elevator you feel lighter but when the elevator gets to the bottom you’ll feel suddenly as if you weigh a bunch more due to Newton’s law of inertia. This is like when you’re traveling in a car and hit your brakes and you’re thrown forward; your body is still trying to move forward as the car stops. Same with the elevator.
BUT if the elevator's speed was very fast before, and when it decreases its speed, it's possible to weight heavier, too!
Log in to reply
Think of an elevator crashing to the ground then suddenly breaking before the crash. The person in the elevator would suddenly weigh much more on the scale even though the direction of movement is always down in this case so in the end you can't be sure if the elevator is accelerating up or deaccelarating down.
When Pam steps on the scale there are two opposite forces. Gravity and Normal force n. Normal force is the reaction of stepping on the scale and pushing it downwards due to gravity. These forces are equal as they are Action-Reaction (Newton's Third Law). If n didn't exist, gravity would pull Pam straight to the Earth's core. It is the force the scale measures to measure our weight. If Pam is in an elevator that is moving upwards, the n force decreases. Thus, even though Pam's mass is the same (Lavoisier's Law Of Mass Conservation) her weight changes because the forces applied are no longer equal since the elevator is moving. Thus, the correct answer is A and not C.
Log in to reply
The normal force isn't the reaction of stepping on the scale, it's the scale's reaction to gravity accelerating Pam downward onto it.
Force is due to acceleration, not motion. If Pam is in an elevator that is "moving upwards", but not accelerating upwards, then gravity is the only force acting upon her body, thus the scale would read 60 Kg. If Pam is in an elevator that is accelerating upwards, then gravity and the force of acceleration would act upon her body, causing the scale to read higher.
If the scale is moving upwards and accelerating, then the scale would read higher. If the scale is moving downwards and decelerating, that is, accelerating upwards (against the direction of motion), the scale would also read higher. The most precise answer is that the scale would read higher as long as the elevator is accelerating upwards. Because the choices given only discuss motion, not acceleration, the correct answer is C.
The comments in this thread are posted, after two explanations have been given? All you "sceptics": Please step into an elevator and observe.
It also could have nothing to do with the acceleration of the elevator... maybe she just put on 10 kilograms since she last weighed herself.
Same conclusion I came to, thought this was a logic question.
When in an elevator going down, decelerating to a stop, mass feels heavier than normal. When in an elevator going up from standstill, mass feels heavier than normal. Also, if Pam has had 4 pizzas for breakfast, it is possible she weighs somewhat heavier than normal regardless of what the elevator is doing.
When the elevator is moving at constant velocity, whether that be up or down, the scale would read a constant weight. Since Pam’s measured weight is greater, the normal force must be greater than Pam’s weight, meaning the elevator is accelerating upward. This could mean the elevator is accelerating while moving upward and therefore speeding up, or acclerating upward while moving downward which would result in the elevator slowing down.
As long as acceleration is pointing up, it would cause gravity to have a larger force on her, and hence the scale. Acceleration is pointing up when 1.) the elevator is moving up at an increasing rate or 2.) the elevator is moving down at a decreasing rate.
Or more mundanely, the scales might be broken so we can't really say anything 'for sure'!
She could also have gained, or lost, weight!
I just thought of the fact of the moving atmosphere which should cause no change
Here’s an intuitive, easy to understand soul room without complex formulas
The elevator can be in one of 4 instances: 1) it is moving upwards and speeding up at the same time (it is accelerating positively in the direction of its velocity) 2) it is moving upwards but slowing down ( accelerating in an opposite direction to its velocity) 3) it is moving downwards and speeding up as it moves (same as instance 1 in the opposite direction i.e. the acceleration is still in a positive direction) 4)it is moving down and slowing down as it moves (same as instance 2 in the opposite direction , the accelaration is still negative)
In case 1, imagine a platform suddenly accelerating, lifting up an object. It will weigh less on the scale as it does not have lots of pressure, as gravity is not pushing the object in the scale, since it is moving up and the force of gravity is overcome. Conclusion: it will weigh less.
In case 2) not only is gravity an acting force, but object places more pressure on the scale as pushes into it, but not enough to overcome gravity. This extra force adds to the total weight: Conclusion: it will weigh more.
Case 3 follows the same conclusion as case 1, we are really Intrested in case 4. Since Pam weighs more, we could say it is possible for the elevator to be moving upward (case 2). Keep this in mind
In case 4 imagine you are in the lift and the floor slows down, the scale on the floor will slow down as well, but you kept the same velocity for a bit as the slowing down is sudden and your body wants to keep moving at the same velocity. You will then exert a force on the scale as you push into it with this extra velocity. This is similar to running into a wall, you are moving faster, so you exert more force. This force adds to the weights making you heavier.
There we go. We can see that we could be heavier moving up or down, so we are uncertain which direction it really is.
I disagree The scale marks the normal force
Log in to reply
The scale will change with weight or force of gravity which is why you will weigh less on a scale of the moon for example
Andrew -- What is a 'soul room' ? I have never heard of that before. :-)
The reading of the scale in the elevator is m ′ = m ( 1 + g a ) , where a is the acceleration in the upward direction. In the problem, the measured apparent mass m ′ is greater than the actual mass m , showing that a is positive: Pam is accelerating upward.
However, this does not tell you anything about Pam's velocity (which is equal to the elevator's velocity) There are two possible scenarios:
the elevator is going upward and speeding up
the elevator is going downward and slowing down
Proof that m ′ = m ( 1 + a / g ) :
According to Newton's Second Law, the acceleration of Pam satisfies F net = m a . The net force on Pam is the sum of the normal force, which is measured by the scale; and the downward gravitational force: F net = F n + F g = m ′ g − m g . Equating the two gives m a = m ′ g − m g , which we solve for m ′ to obtain the desired equation.