Lifting Rope.
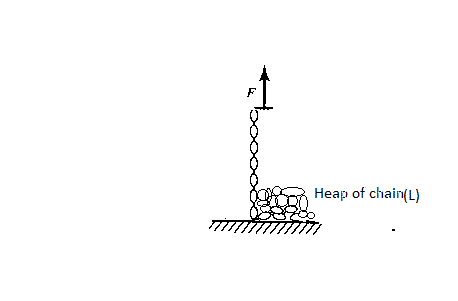
A rope of length l and mass density λ lies in a heap on a floor. You grab one end of the rope and pull upward with a non-impulsive constant force F o . Find the time period require to completely lift off the rope.
Assume that the rope is greased.
The answer is in the form T = g a ( λ F o − λ F o − c b g l )
Find a + b + c
I got this question from Deepanshu .
:D
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Nice solution bro. That diagram looks good to me. :D
Log in to reply
@satvik pandey - bro please remove pulled "slowly" from the problem, it is confusing, whether we should neglect v or not, i lost one chance thinking slowly means dv/dt = 0 as if v = 0 (my other thought) then answer was not in ur form.
Log in to reply
Sorry ,But actually I add this word "slowly" . Because I thinks when we pulled this fastly then May be Tension should not be zero at the Lower end ! what did u say ?
But Now I added That It should be " Non-Impulsive " Is it Ok Now ?
@Mvs Saketh
Log in to reply
@Deepanshu Gupta – well,i think as long as we are pulling it straight up and all the mass of the heap portion is supported fully only by the normal reaction of the ground, then speed is irrelevant, Infact pardon me if i am wrong, but tension is not 0 at base, there is an impulsive tension force due to the varying mass, i think you mean to say that tension is not created due to the mass of the heap, yes that is necessary, but its fine :)
Log in to reply
@Mvs Saketh – I have a confusion. I agree that Tension acts at the base of the chain due too sudden change in velocity of the last link but why do we neglect that in writing the equation ( F n e t = d t d p ) if the chain is heaped on the floor. We don't do so if the chain is lying straight on the floor.right?
Log in to reply
@Satvik Pandey – If chain is lying straight, then it is a must that all links lying on direction must move at the same speed along a linear direction, and hence the last link doesnt suddenly change its speed at the point where it rises (that is was moving all along), kinda like the constraing motion in pulleys ,
However if it is heaped, the links need not have velocities along the chain at all instants, they can slightly snudge to the right or left and adjust and thus for all practical purposes, (and for sake of making such a problem) (and still keep it solvable) each link in heap can be said to be at rest
Log in to reply
@Mvs Saketh – Thanks for explaining. :)
@Mvs Saketh – @Mvs Saketh , the last link dosen't suddenly change its speed but velocity is indeed changed and as the string is not massless(as in constrained motion) , a force would be required for the change in momentum. Is this right, if not, what is the counter-argument, bro?
guys, check out my solution, I got a different answer http://www.mediafire.com/view/31kw63c8dkua9ek/12mv2.docx I didn't add any explanation because my english is bad, but I think you guys can still get the idea
Truly cool problem.
i am getting different answer by energy conservation. i got same answer which nam cao got! can anybody clarify
Log in to reply
I also used conservation of energy and got the same expression as given by Nam Cao in the Word document he has linked to.
note that v is the COM velocity of the lifted portion of the rope , so v = 2 x ˙ = d t d 2 x
Let The at t=t , 'x' length of rope is pulled by us and let it be as our system which is uplift by us in presence of gravity , and at the Lower end of rope there is heap of rope so no Tension act's at the end of heap. Using Laws of motion of Newton Sir (Here F = m a does not Valid, Because it is not an closed system )
F o − λ g x = d t d ( λ x v ) F o − λ g x = λ v d t v d ( x v ) ( ∵ v d t = d x ) ( F o − λ g x ) x = λ d x x v d ( x v ) ( m u l t i p l y b y ′ x ′ b o t h s i d e ) ∫ 0 x ( F o − λ g x ) x d x = λ ∫ 0 , 0 x , v x v d ( x v ) By integrating we should get ( v = λ F o − 3 2 g x ∫ 0 l λ F o − 3 2 g x d x = ∫ 0 T d t Now Evaluate This Elementary integral we should get T = g 3 ( λ F o − λ F o − 3 2 g l )
I had added an Image to This Problem , Can you please confirm it ? Is it Ok