Blue Area?
This triangle is divided into nine parallel stripes of equal height. The total area of the red stripes is 145.
What is the total area of the blue stripes?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
41 solutions
Thank you, nice solution.
It's a really nice solution. I like it!
Learned from it! Elegant Solution.
My goodness
So damn good.
is this possible? i a also think that way
very clever!
I was able to uncover the ratio by playing with the numbers although I was not able to justify with confidence that it was correct. Your answer makes it clear. Thank you!
Why are you so genius?
Exactly how I did it.
Why does this follow the general 80/20 principle (in the alternative solution)? Is there an actual mathematical correlation?
Awesome!!! Seriously Very Good
Cool solution!
My solution was similar but slightly less elegant; I rotated the top half of the triangle 180° to form a parallelogram with stripe ratio 2 blue : 2.5 red
Log in to reply
I wouldn't call it "less elegant". Your solution keeps both colored areas unchanged.
If we have 9 total equally divided horizontal sections ... and four of them one color and five of them a different color, then the ratio of the the horizontal sections should be 4/5 of the total area. 145 x 4/5 = 116. This applies equally well to two triangles to form a parallelogram as well as one triangle. I really like the parallelogram visualization because it makes the partitioning of the trapezoids into congruent sub-parallelogram much easier to visualize.
blew my minds dude!
Ok, it works with an odd number of strips, but what if there was an even number?
Log in to reply
With an even number of strips, no parallelograms would be formed. For that problem I would figure out a different approach!
Genius! These are always amazing solutions!
Thanks for the solution
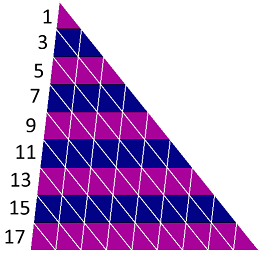
Just for the variety of approach, the strips are forming an AP 1, 3, 5, 7, 9, 11, 13, 15, 17 To see this more clearly, draw lines parallel to the two sides, dividing the large triangle into little triangles congruent to the top red triangle!
The red are terms 1, 5, 9, 13, 17 adding up to 45 and blue 3, 7, 11, 15 adding up to 36
So the blue area = 36 x 145 / 45 = 116
This is how I did it.
wow. how though.
used the same method ;)
Triangules' ratio = (number of strips + 1)/(number of strips - 1) >> (9 + 1)/(9 - 1) = 1.25 >> 145 / 1.25 = 116.
The diagram shows nine overlapping triangles that share the same top vertex with all of their bases parallel. These nine triangles are similar to each other, so their areas are proportional to the squares of their heights. Suppose the smallest triangle has area A.
Then the triangles have area:
1 2 A , 2 2 A , 3 2 A , 4 2 A , 5 2 A , 6 2 A , 7 2 A , 8 2 A and 9 2 A .
Thus, the area of the red stripes is A ( 1 + 3 2 − 2 2 + 5 2 − 4 2 + 7 2 − 6 2 + 9 2 − 8 2 ) = 4 5 A .
Similarly, the area of the blue colored stripes is A ( 2 2 − 1 2 + 4 2 − 3 2 + 6 2 − 5 2 + 8 2 − 7 2 ) = 3 6 A .
Therefore; the ratio of the area of the red stripes to the area of the blue stripes is 3 6 A 4 5 A = 4 5 .
Thus,the total area of the blue colored stripes is 5 4 × 1 4 5 = 1 1 6 .
This is the way I did it. I'll admit it's less elegamt than the top solution but it definitely works well
Ugh. I’m so not into math. 😖
Each of these triangles have heights h/9, 2h/9, 3h/9, 4h/9......9h/9. so the Area of the first triangle is 0.5 * b1 * h//9 the second is 0.5 * b2 * 2h/9. So how are these areas propotional to the squares of the heights...Is it a corollary of any known properties of Similar triangles ?
Log in to reply
Since triangles are similar, for first two triangles for example, b2 is twice of b1. That will introduce a factor of 2 and hence it will be 0.5 * 2 * b1 * 2h/9. This will give the factor of 4 when compared to area of smallest triangle. if you do it so on and so forth, comparing why smallest triangle every time you will realize it will come to being proportional to square of 3, 4, etc
Log in to reply
Okay got it mid point theorm. Thanks for the explanation.
Log in to reply
@Srinivasa Gopal – @Rishabh Biyani Thank you for the explanation. @Srinivasa Gopal , l hope is it clear now and I apologize for missing your comment.
I thought you had to count the number of red strips in the denominator making it 4/9...
Log in to reply
We are taking into account the red strips number in some way.
you completely lost me as soon as you started calculating the triangles' areas. what is happening?
Log in to reply
I wanted to come with a different approach so l took the areas of triangles. We know all the triangles are similar and if we consider the ratio of proportionality, we obtain the above scenario. I hope this was helpful.
I did this in a whole different and,admittedly, long way. I first took out all the
5
red stripes and arranged them to make a triangle and then the
4
blue stripes to make a trapezium.
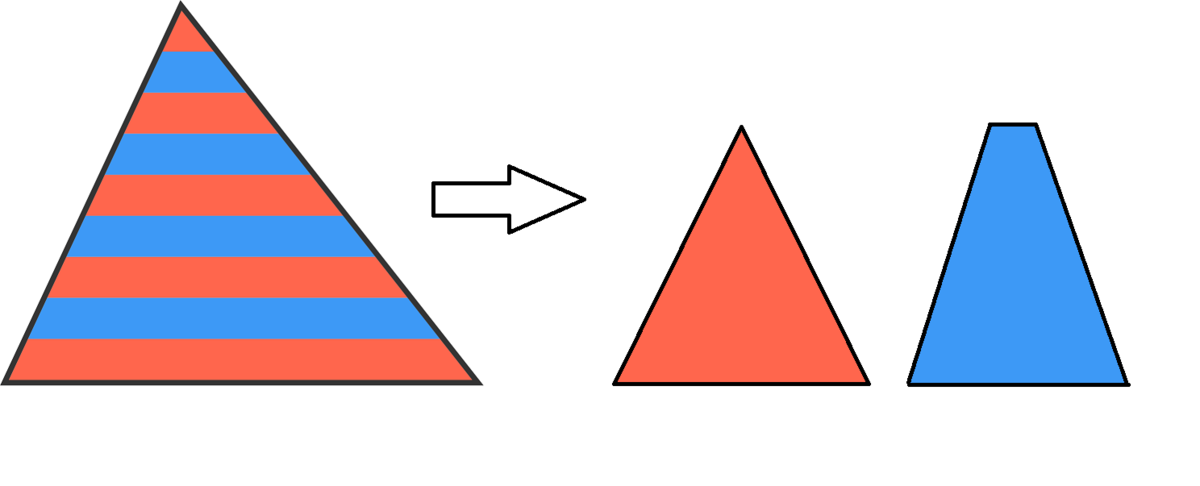
Now, we have two shapes to work with. All we need to do is to find the area of the trapezium.We also know that the total area of these shapes is that of a triangle with base equal to the base of the red triangle (Let's say " b ") and height equal to nine times the width of a single stripe (Let's say " h ").
Basically, we have, 2 1 x b x 9h = 2 1 x b x 5h + Area of the Trapezium. ...........(i)
Now, we know, 2 1 x b x 5h = 145 .....................(ii)
Therefore, b x h = 145 x 5 2 = 58
Now taking this in account, in the equation (i),
0.5 x 9 x 58 = 145 + Area of the Trapezium
Area of trapezium = 261 - 145 = 116
Therefore, Area of all the Blue stripes = Area of the Trapezium = 116
Triangules' ratio = (number of strips + 1)/(number of strips - 1) >> (9 + 1)/(9 - 1) = 1.25 >> 145 / 1.25 = 116.
Log in to reply
You're right.I just took a "good enough" approximation of that. I'm sorry that I forgot to mention that fact earlier.
Similar to @Arjen Vreugdenhil 's Solution:
I converted the triangle into two right triangles . From there, by doubling both the right triangles, then flipping then vertically, a rectangle is formed. This allows you to confidently determine that the red makes up 9 5 of the total area, where as the blue makes up 9 4 . Diving the red portion by 5 ( 5 1 4 5 ) gives you 2 9 , which makes up 9 1 of the total area. Multiplying 29 by 4 then gives you the total area of the blue stripes.
Triangules' ratio = (number of strips + 1)/(number of strips - 1) >> (9 + 1)/(9 - 1) = 1.25 >> 145 / 1.25 = 116.
Threre's 4 blue stripes to 5 red stripes, so therefore 5 4 ⋅ 1 4 5 = 1 1 6 What's wrong with that?
Makes sense to me.
Cool. It works as long as the stripes have equal width and the order of the colors is palindromic. It's a nice relation, even if I had to think a bit about why it works.
Yes, what's wrong with that reasoning?
This reasoning is wrong, because each stripe has a different surface area. But by doubling in the way shown, the area of all stripes are equalized in a valid way...
ha ha ur right
Log in to reply
never mind, the surface area is a BIG difference the stripes are not equal though
So if you add one more blue stripe at the end the total blue will be 145 as there are equal count?
Log in to reply
Then the order of the colors wouldn't be palindromic.
Log in to reply
Yes and the statement will not be true. It is true only for odd amount of stripes - and this is what is "wrong" (missing). * Sorry i did not see your answer! :(
Log in to reply
@Milko Dyakov – That's a little too restrictive for me, all that is necessary in general is the sequence is palindromic. There's no reason I see to disallow two consecutive stripes having the same color or the triangle having more than two colors, when we're already generalizing.
Log in to reply
@Brian Moehring – And this is very true. I can see that I am wrong - palindromic color sequence fits much better. I am already double sorry for my comment :/ Thanks for the note !
Triangules' ratio = (number of strips + 1)/(number of strips - 1) >> (9 + 1)/(9 - 1) = 1.25 >> 145 / 1.25 = 116.
It's wrong: supposed there were 2 and 3 strips, the ratio would be 2/4, not 2/3.
Log in to reply
Sorry, Andre, but by your own formula, the ratio = (number of strips + 1)/(number of strips - 1) >> (5+1)/(5-1) = 1.5 so it is indeed 2/3 not 2/4. :-|
Log in to reply
Sorry, you're right. For some reason I made that mistake. My formula is correct, and works with both odd and even numbers of stripes (of course, would the number of stripes be odd, you'd just divide it by it-1). Using the same triangle: knowing that the blue area=116, the area of the first 4 red stripes is 116 * (7/9) = 90.2222222.
easiest and simplest way , good job bro
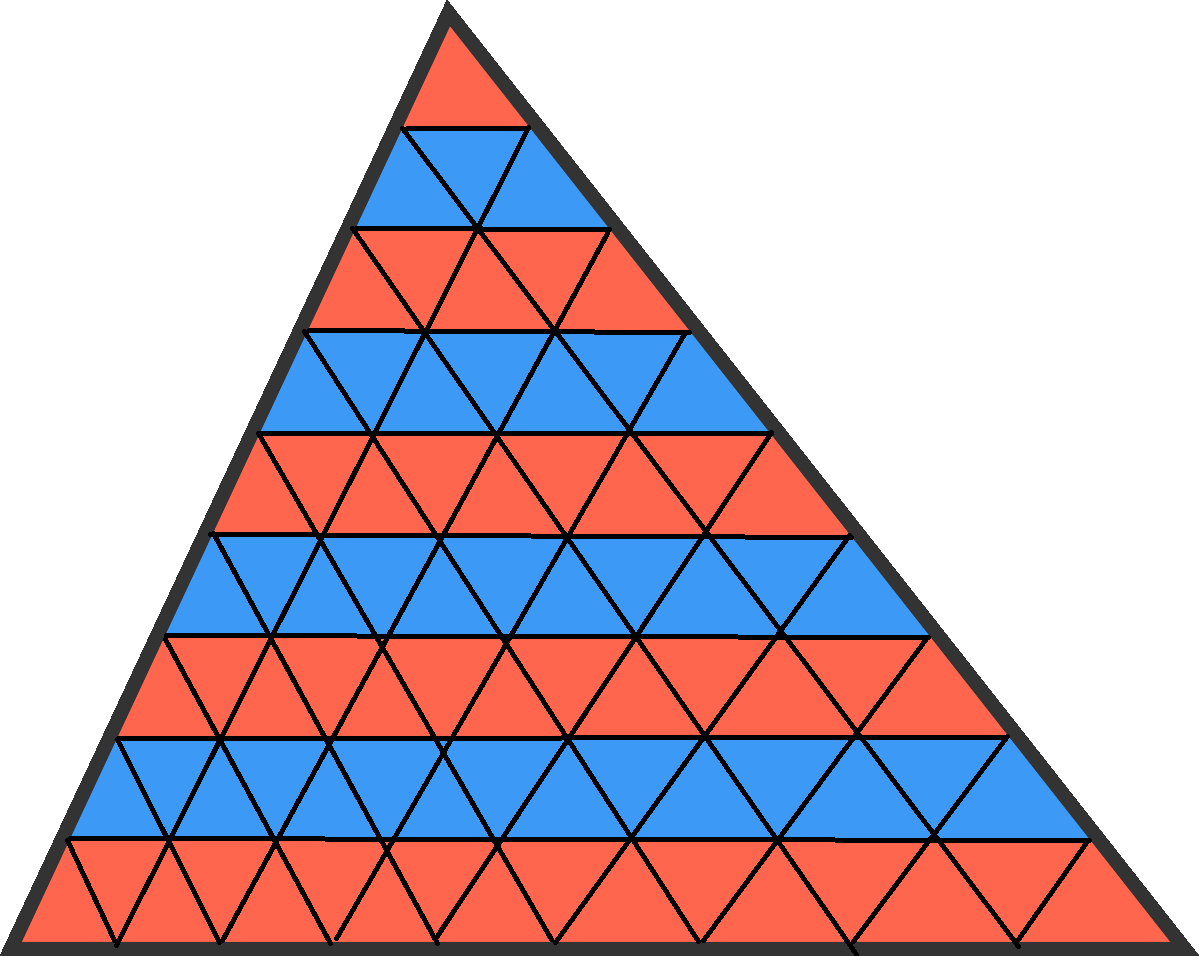
Using all congruent triangles, we have 45 red triangles, to 36 blue triangles. Proportionally 1 4 5 ⋅ 4 5 3 6 = 1 1 6
Triangules' ratio = (number of strips + 1)/(number of strips - 1) >> (9 + 1)/(9 - 1) = 1.25 >> 145 / 1.25 = 116.
It can be solved by simple use of average. The area of middle strip among the red colour is the average of all strips of red colour. So the area of middle red strip is 145/5 = 29. Also , area of every blue strip is the average of those red strips in between it is placed. Thus , using this approach we get the answer as 145/2 + 3×29/2 = 116
Extend the stripes to make a rectangle, which is made up of 9 equal stripes. Here is the following working: 145•2=290 290/5=58 58•9=522 522/2=261 261-145=116 So the area of blue stripes is 116.
The total area of the red stripes is 145, which means that if partitioned into equal areas, each would represent an area of 29. 145/5 = 29. You could think about the blue areas as being equal to the red areas except one of the blue areas is missing so 145 - 29 = 116.
The solution is very simple, all you have to do is divide the area of the red stripes by how many red stripes there are. Get the answer, which is 29, and times it by four OR take away 29 from the area of the red stripes. (Becuase there are 5 red stripes and 4 blue stripes.)
Lengths of horizontal lines are in proportion, being bases of similar triangles, so if the first one on top is a , next is 2 a , etc.
Heights of triangles with those bases are also proportional, b , 2 b , etc.
So the red area is: 2 1 ( a ⋅ b + ( 3 a ⋅ 3 b − 2 a ⋅ 2 b ) + ( 5 a ⋅ 5 b − 4 a ⋅ 4 b ) + ( 7 a ⋅ 7 b − 6 a ⋅ 6 b ) + ( 9 a ⋅ 9 b − 8 a ⋅ 8 b ) ) = 2 4 5 a b = 1 4 5
Therefore a b = 9 5 8
The blue area is: 2 1 ( ( 2 a ⋅ 2 b − a ⋅ b ) + ( 4 a ⋅ 4 b − 3 a ⋅ 3 b ) + ( 6 a ⋅ 6 b − 5 a ⋅ 5 b ) + ( 8 a ⋅ 8 b − 7 a ⋅ 7 b ) ) = 2 3 6 a b = 1 8 a b = 1 8 ⋅ 9 5 8 = 1 1 6
Thank you, nice solution.
The stripes are congruent; they are in the same ratio throughout the triangle. There are 5 red stripes to 4 blue stripes, thus they are in the ratio of 5 to 4. If the area of the red stripes is 145, then the area of the blue stripes would be 145/5 x 4= 116
5 stripes red // red stripes(5)÷ total area of red stripes (145)= 29
4 stripes blue // area per red stripe (29) × number of blue stripes (4)=116 / 5 ÷ 145 = 29 29 × 4 =116 /
the average area of each stripe is equal, for red it is 145:5=29, blue total area would be: 29*4=116
Because all the stripes are of equal height and parallel, they have the same average area. So, I divided the total by 5 to get the average area of each stripe. 1 4 5 / 5 = 2 9 . Then I multiplied by 4 for the total area of blue. 2 9 ∗ 4 = 1 1 6
I observed that you have 40(LX H') + 5(2LX H') = 145 and 32(LX H') + 4(2 L X H')= b L time H being a rectangular surface, while 2 time L time H' being the little red triangle. which gives us a ratio of 0.8
I'm not sure if this is mathematically correct, but I solved for total area as 5 red stripes to 9 stripes total. So 5/9 x = 145. Total area = 261. 261- 145 = 116
its a negative approach.i tried using two given things equal strip width to my advantage and shape of the figure. as area of triangle is 1/2 * base * height, where height = 9 * width of one strip, so area of triangle is 9 * (1/2 * base * width)..so for area to be multiple of 9, sum of its digits must be divisible by 9 too . 145+trying each option gives only one possible answer of 116 obeying the above stated idea(number theory principle) i.e.145+116=261 implying 1+6+2=9 rest are 265(sum=13),290(sum =11),280(sum=10).
If the total area of the red stripes is 145 and there are 5 red stripes I know the area of each red stripe: 5 1 4 5 = 29. But I know that all stripes have equal width so 29 is the area of each blue stripe too. There are four blue stripes so their total area is 29x4 = 116.
Am I right?
You can double the triangle. Then there are 5 red and 4 blue stripes. In one triangle the area of the red stripes is equal to 145. So in our "doubled triangle" the total area of the red stripes is equal to 290. Then we can say: 9 5 *x=290 <=> x=522. So x is the total area of our parallelogram. Now we just multiply x=522 with 9 4 for the total area of the blue stripes in our parallelogram and divide it by two to get the final answer: 9 4 x522=232 and 2 2 3 2 =116
Think of the very top red triangle as one unit. Then observe that the number of units per shape counting downward is 1,3,5,7,9,11,13,15,17. Adding up the total red units gives: 1+5+9+13+17=45. Adding up the total blue units gives 3+7+11+15=36. Since the red area is 145, we set up the ratio 45/145 = 36/X, and we solve for X to get 116.
I think my solution is the easiest:
Be 9 stripes made of 5 red and 4 blue We know red is equal to 145, it's a simple cross product. 9 4 =145; 9 5 =x; x= 5 4 ∗ 1 4 5 ; x=116. QED
So I somehow solved this by going at the problem completely different (and probably wrong) than from what I've seen. So when I first read the problem, I misread and thought 145 was the total area of the triangle. Then I went ahead and knowingly assumed that each stripe was equal in size and area even though they are not.
So my brain first went to figure out what 145 divided by 9 was (since there are 9 stripes total and I was trying to dividing equally assuming each stripe was equal in size and area) and "tried" to chunk it first. 45= 9 x5 and to get 100 you do 5x 20 . So my "Area" of each stripe was 29 . I then took 29 and multiplied it by the number of blue stripes which is 4 ( 29x4 ) and somehow ended up with the correct answer, 116 .
As I type this and reread what I typed and how I went about to get the answer, it just makes no sense. I guess you can say I got lucky?
145 / 5 ( Reds) = 29 ( width of one red stripe); therefore 29 is the width to multiply by 4 stripes ( blue ) = 116
In such a triangle,the number of red to blue stripes must be in a common ratio(which turns out to be the case,i.e, 4:5)
In addition to this,when there is no triangle,there is no area.The ratio of the number of red stripes vary proportionally with the number of blue stripes,as well as,the whole figure.Irrespective of the area,the number of red or blue stripes or both,the figure must always end in a way such that the ratio of the number of red stripes is 1 more than the number of blue stripes.
In the diagram,the ratio is 4:5.
Likewise it would be 3:4, 2:3, then until it eventually becomes 1:2.
Or increasingly become 5:6, 7:8, then 8:9,and on it goes...
The more stripes,the more the area.
Therefore using simple probability
5 red stripes =145 1 red stripe =(145÷5) =29
Both ratios can be in their simplest form by dividing both areas by 29.So,in order to find the area of the blue stripes,multiply the ratio of the number of blue stripes with the common ratio,i.e,
Area of blue stripes =29×4 =116
There are 5 red strips out of 9 So 5a=145 so a=29 . There are 4 blue strips so 4a=4*29=116
The area of a trapezium is half its height times the sum of its parallel sides. Therefore the area of a set of equally high trapeziums is half the height times the sum of all their parallel sides. If we see a triangle as a trapezium with only one "parallel side" then all 9 stripes are trapeziums. By geometric similarity the lengths of their parallel sides are 1, 2, 3, 4, 5, 6, 7, 8 and 9. Every parallel side of a red trapezium is also a parallel side of a blue trapezium, except for the bottom one. Therefore the total area of the blue stripes is
b l u e = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 × r e d = 4 5 3 6 × 1 4 5 = 1 1 6
First horiz. line bw. r and bl: Length a;
Second line length: 2a, ...
Each trapezoid height: h
With given area of all RED trapezoids from top to bottom: ((0+1)+(2+3)+... +(8+9)) a h/2=145
find area of all BLUE trapezoids from top to bottom with: ((1+2)+(3+4)+... +(7+8)) a h/2=?
Must be 116.
Just count the lines, there's 5 red and 4 blue lines.
5 : 4 and under the number 5 goes 145, and under 4 goes x, and out of those you get:
5x=4*145 x=116
Using the knowledge that the area of a triangle is 1/2 * b × h, apply a unitless value of 1/2 to the area of the top red triangle. For the second row, the blue rectangle area directly beneath the top red triangle then has a unitless value of 1. The triangles that are the ends of the second row sum to a unitless value of 1/2. For the third row, the area under the rectangular area of row two has a unitless value of 1. The two rectangular areas under the end triangles of the second row add together to a unitless value of 1. Again, the two end triangles add to a unitless value of 1/2. Continue doing this for each row. The row sums are then... 0.5, 1.5, 2.5, 3.5, 4.5 ,5.5, 6.5, 7.5, and 8.5. Add the row values for each color. Red = 22.5, Blue = 18. The ratio of blue to red is 18:22.5. Blue area = 145 * 18 / 22.5 = 116.
First, I asked myself what times 5 gives me 145? I tried random set of numbers like 27 5, 28 5,29 5 to find the two sets that would give me 145. Turned out 29 5 is 145. So I found the two value length, and just multiplied by the 4 stripes of blue.
Was I the only one who didn't think of over complicate this question? 5 1 4 5 =29
29 x 4 ( amount of blue stripes) =116
Given: Graph RED area = 145 The height for all shaded areas are equal.
All of the shaded areas are trapezoids. Find the areas of trapezoids using the formula (½)h(b1 + b2). Since the heights of each shaded are equal and there are nine of them, each shaded area has the area of 1/9 of the total area.
Triangle is a special case where b2 = 0
The 5 RED areas equal 5/9’s of the total area. OR, (5/9)(Total Area (TA))= 145 => TA = 261.
Subtract the RED area from TA , RED-TA => 261-145=116
As a check 4/9(TA) => (4/9)(261)=116
Total area 145 divided by the 5 red segments results in 29. Multiplied by the 4 blue segments results in 116
Assume the base of the triangle is 9 units and the height of each strip is h. Then each stripe is a trapezium, including the degenerate trapezium (triangle) at the top. The area of a trapezium is (sum of parallel sides) * height/2.
Thus the red stripes have area (0+1)h/2 + (2+3)h/2 + ... + (8+9)h/2 = (0 + 1 + 2 + ... + 9)h/2. = 45h/2.
The blue strips have area (1+2)h/2 + (3+4)h/2 + ... + (7+8)h/2 = 36h/2.
The ratio of areas is thus (36h/2)/(45h/2) = 4/5 so the blue area is 116.
pretty easy lol, make into parrelogram, by double the triangle, 5/9=290, and 4/9=x. Solve for x, using ratio 5:4
I could solve it using the 8 trapezoids in the triangle# 4 for each color # height : h (one stripe)# the smallest base : z # all triangles are similar to each other so their bases are similar too. # area of the trapezoide = [{(nz+(n+1)z)}/2]Xh # area of the smallest triangle = 1/2 X zh # so area of the red stripes = 45/2 zh =145 ## zh = 6.44444........ ## area of the blue stripes = 18 zh =18X6.4444.... = 116
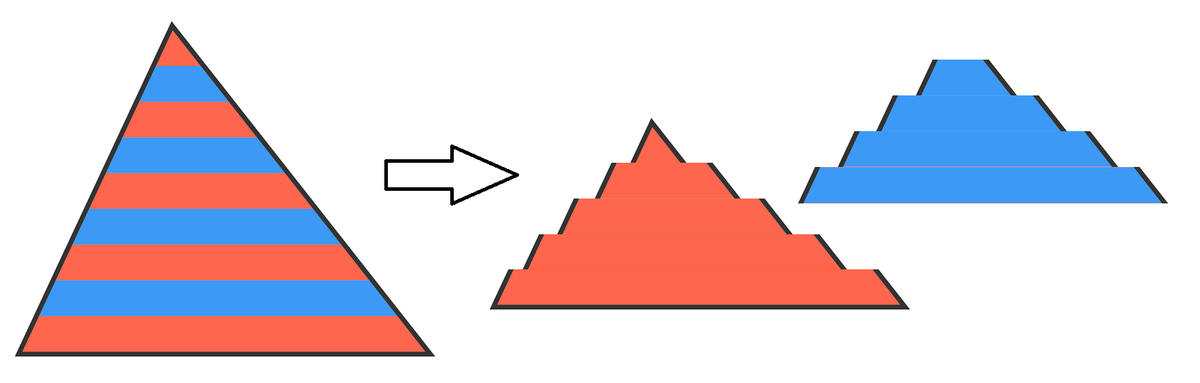
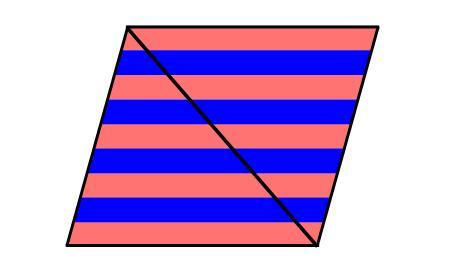

The easiest way is to double the triangle in a clever way (which, of course, does not change the ratio of areas).
Now we have nine congruent parallelograms. They have the same area, so blue : red = 4 : 5 = 1 1 6 : 1 4 5 .
Alternative
The area of each strip is proportional to its width, which in turn is proportional to its distance from the top vertex.
Note that on average the blue strips and red strips are at the same distance from this top vertex. Therefore their average widths and averages areas are also the same. This means that the ratio of blue and red areas is equal to the ratio of numbers of red and blue strips.