Let's play Football
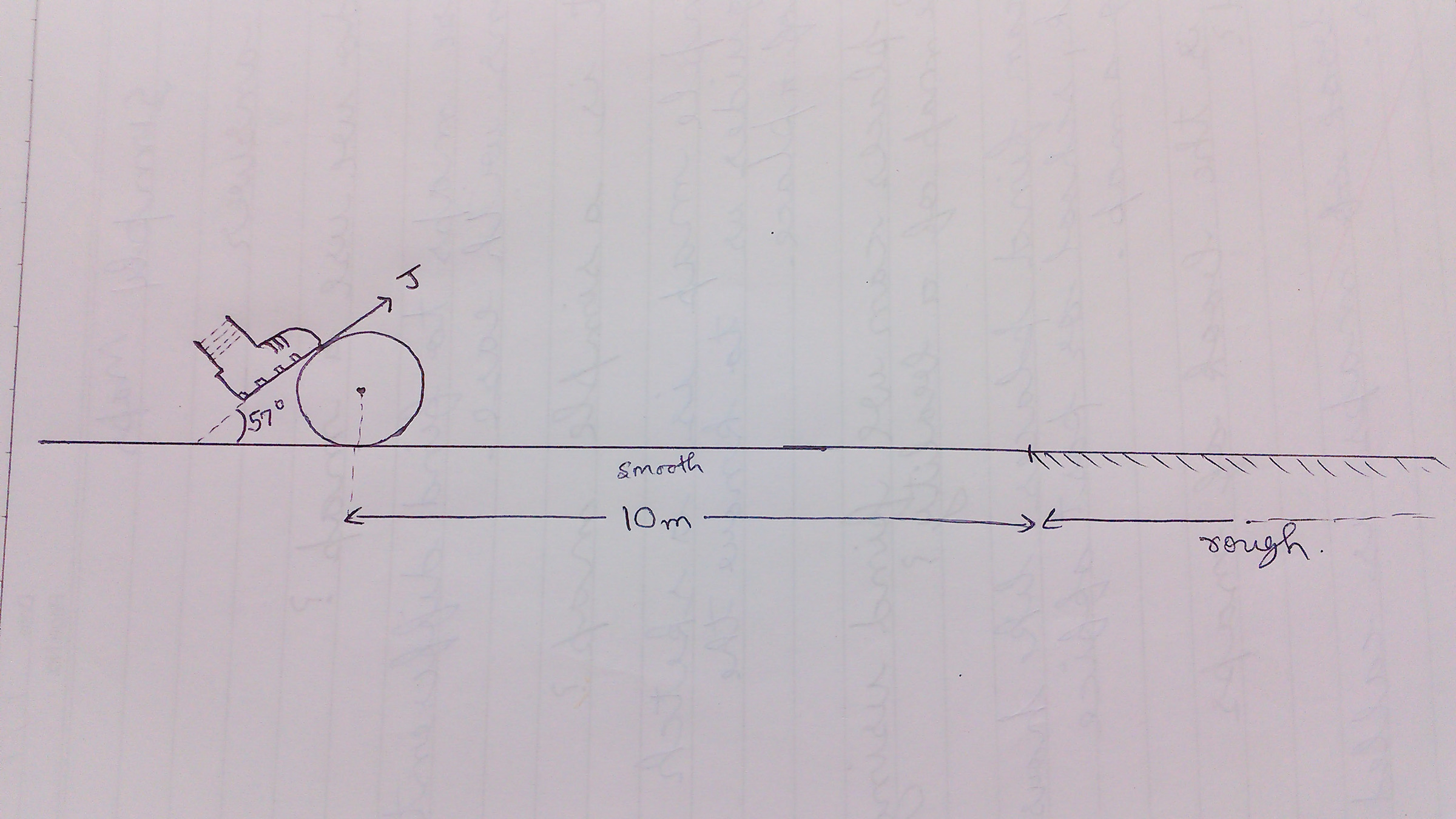
You kicked your football ( solid sphere ) as shown in the figure. You apply an impulse (J) as shown(sorry! Angle is 53 degrees ) .
What will be the Final displacement of the ball (i.e. when it's vertical velocity tends to become zero) from the initial position( in metres ).
Details and Assumptions :
-
The surface is smooth below the ball ,where it is placed. The rough surface starts at a distance of 10 metres from initial position of ball and continues to infinity .
-
Given, mass of ball M = 0 . 5 0 K g , Radius of ball is R = 0 . 2 0 m , J = 5 N − s (at an angle of 53 degree as shown), take g = 1 0 m / s 2
-
Coefficient of restitution ( for vertical collision ) = 0.5 , and coefficient of friction of rough ground is 1.0
Try more here
The answer is 23.542.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
If you like it! Then don't resist to like it! Share it! And upvote the solution
Log in to reply
My further Analysis has the following results
After Collision with rough ground if friction is sufficient for the ball to roll purely then at the time of second collision we are left with the following two possiblities
-
Friction Do not act In third , fourth... collision with the ground as condition of pure rolling will always get satisfied if friction does not act as the frictional impulse was the only one which was responsible for change in horizontal velocity and angular speed of the ball.
-
Friction Being a self Adjusting Force Will Adjust itself in such a way that during each of collision even after changing the horizontal velocity and angular speed of the ball the condition of pure rolling gets satisfied.
Your solution Takes into consideration only 1st case. On further Analyzing second Case I Found That this thing can also happen as i found out some velocities are fourth and 5th collision and Found friction to be sufficient. Expecting A Nice Reply :)
One more thing i want to point out is that When friction is involved in collision then Line of impact is not vertical as far as i know it will be inclined to the surface. So How can we use normal reaction in vertical direction
@Avi Ghanshani , @Aniket Sanghi , @neelesh vij
Log in to reply
I don't understand your second case at all , in the second collision after the condition of pure rolling is satisfied ,if the friction will act again for third collision it would make tball stop pure rolling you can see it yourself ....if v increases omega would decrease
Log in to reply
@Aniket Sanghi – Is it necessary pure rolling to always take place? cant it slip in between
@Aniket Sanghi – or can't it happen like friction acts in backward direction such that its velocity in horizontal direction becomes zero?
bro, great question ! +1 for both solution and question ! you rock !
Bro there's a mistake (A BIG ONE) the angle should be 53 degrees not 57 degrees. You are getting the same values when the angle is 53 degrees. Please change it. I took 53 degrees as it produced very simple values as compared to 57 degrees.
Great question btw. A similar question was posted by ronak also.
Did it the same way......I want to ask can there be some value of e and coefficient of friction for which pure rolling never begins.
Log in to reply
Nice question!
If you think logically it is not possible if you allow ball to go to infinity, 2 cases may arise either a complete halt or pure rolling because even if the coefficient of friction is too less to stop relative motion but it's motion to infinity (infinite collision)will certainly give it a large value that is net effect is large ..........
I have not proved it mathematically , If I could find something interesting I will soon post a q related to this........
Log in to reply
Well, logically it seems correct but, as the impulse due to normal force is decreasing, so when I sumed the GP to infinity and imposed the condition of pure rolling , I was getting a relation between e and k(coefficient of friction) . And I wanted to say that it will not start pure rolling after some finite collisions. In this question please analyse the case when coefficient of friction is less than 19/42.
Got the conclusion! It is not possible at all if we take values very small then too due to infinite collisions it will stop slipping in infinity
Do you like the question? Then reshare to give others the chance to attempt it
I Cannot understand why frictional impulse won't act for successive collisions @Aniket Sanghi I Solved Till R3 = 32/7 And got struck
I Got my mistake But here are some points i am not still clear about
- If i assume frictional impulse to act at third collision , i found that friction is not sufficient for pure rolling. Hence Slipping can take place at third collision where in impulse due to friction = mu(impulse due to normal reaction)
so in this way the ball can slow down @Aniket Sanghi @aryan goyat @Prakhar Bindal
Log in to reply
Actually friction is sufficient in second collision for pure rolling and when pure rolling starts frictional force don't do any work on it so horizontal velocity will not change after third and successive collisions
Log in to reply
My point is that Why cannot Slipping START AT The THIRD Collision.
This is one of the best problems i have solved on brilliant!. I Revised rolling concepts from my notes then i was able to solve it after 1 wrong attempt. Keep Going!
Log in to reply
Its not only rolling. Its Also Collision!! This question thrilled me :)
I have a lot of doubts. First one being,how do you know friction is sufficient for pure rolling?
Log in to reply
You can check it !! :)
Log in to reply
Ohk,you mean by putting values?
Log in to reply
@Adarsh Kumar – By calculating mu for this case
Log in to reply
@Aniket Sanghi – Ohk!So that is one doubt cleared,now my next doubt is,why is frictional impulse 0?I get that work done by f is 0 but f has a magnitude,then why is f dt =0?
The required friction was as I can recall 19/21 (mu)
exactly same as your solution !
Can u please tell me how is friction sufficient for pure rolling u required comes out to be 19/21 but u max is only 0.1
Log in to reply
Read it again , μ m = 1 . 0
Good question!!! Nice ..
Log in to reply
True, Awesome question
Log in to reply
The level of his Mechanics problems reflects why he is in IIT Kanpur today. BRILLIANT
Log in to reply
@Ankit Kumar Jain – Hmm... Dont worry, IIT's are also waiting for you
Log in to reply
@Md Zuhair – You are the one for whom IIT is waiting for... @Md Zuhair
First of all , due to impulse
Horizontal velocity V x = 6 m / s e c
Vertical velocity V y = 8 m / s e c
Angular velocity ω = 1 2 5 r a d / s e c
Before the first collision ,range travelled is R 1 = 9 . 6 m ( < 1 0 m )
Since it is less than 10m , hence it is still on the smooth surface, friction is 0. (Normal collision)
In between first and the second collision , it travelled a further range of R 2 = 4 . 8 m
Now the friction is there.... It is sufficient to cause pure rolling
F d t = m ( v − V x )
F R d t = 5 2 m R 2 ( 1 2 5 − ω )
And ... ω R = v
You will get v = 7 8 0
In between the second and the third collision, range travelled is R 3 = 7 3 2
Now , since their is no slipping therefore no frictional impulse will act for the successive collision(i.e. For the third , fourth and so on)
Range forms the series R3 + R4 + R5 + .... = 7 3 2 ( 1 + e + e 2 + e 3 + . . . . . ) = 9 . 1 4 2
Hence final displacement is R 1 + R 2 + R 3 + . . . . = 9 . 6 + 4 . 8 + 9 . 1 4 2 = 2 3 . 5 4 2