Limit of The Tower

Compare the graphs of $y=a^x$ (in blue) and $y=x$ (in red). It is a straightforward exercise in calculus to show that for $1<a<e^{1/e}$ the two graphs intersect at two distinct points, for $a=e^{1/e}$ the graph of $y=x$ is tangent to $y=a^x$ at $x=e$ , and for $a>e^{1/e}$ the graphs do not intersect. Now use a cobweb representing the iteration to see that for $1<a\leq e^{1/e}$ the sequence $a_n$ converges to the (lower) point of intersection (the sequence is increasing and bounded), while for $a>e^{1/e}$ it diverges to infinity as it is increasing without fixed points. See the two attached pictures.

Thus the answer is $a=e^{1/e}\approx \boxed{1.445}$

suppose the limit is $L$ , then it must satisfy $a^L=L \implies a=L^{\frac{1}{L}}$

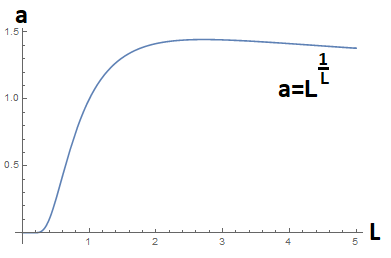
from graph, $a$ has a maximum value, which can be found easily using derivative.

$\begin{aligned} a &= L^{ \frac{1}{L} } \\ \frac{da}{dL} &= x^{ \frac{1}{x} - 2 } (1 - \ln x) = 0 \\ (1 - \ln x) &= 0 \\ x &= e \\ a &= e^\frac{1}{e} = 1.44467 \end{aligned}$

We can extrapolate out of the given information that the series will have to respect the equation $L = a^{L}$ as n goes to infinity. L represents the limit of the series and a simply is the value of a in the problem. The question then become really simple : what is the highest pair of variables L and a such that this equation holds? In order to do so, we do the derivative of $a = L^{1/L}$ . We get this equation : $(1-Ln(L))*L^{(\frac{2L-1}{L})}$ We wish to find the value of L when this equation is equal to zero as this will give us the highest point of the function. This gives us $L=e$ . Then we just go back to the first equation and plug e into the it, which gives us that $e=a^{e}$ , from which we can find that $a=e^{1/e}$ which is our answer.

The limit, let’s call it $x$ , is that of an infinite tower of exponentiations of $a$ . If the limit exists, then we have $a^x = x$ .

The graphs for $y =a^x$ are well-known exponential curves, and for $y = x$ it is a straight diagonal line through the origin with slope $1$ . For $a=1$ these graphs clearly intersect, and for $a=2$ they don’t. For values of $a$ between 1 and 2 there can be zero, one, or two points of intersection. For the largest value of $a$ where they still intersect, these graphs have a single point of intersection, and they touch each other (are tangent to each other). Note that the derivative of $a^x$ equals $a^x \log a$ .

Thus we know $a^x = x$ and $a^x \log a = 1$ . Substituting the first in the second yields $x \log a = 1$ , hence $a = e^{1/x}$ . Substituting this in the first and simplifying yields $e = x$ . Hence, \fbox{\$a = e^{1/e} \approx 1.4447\$} .

If a(0)=a, then a(1)=a^a,a(2)=a^(a^a), a(n)=a^(a^a...(n times)). Now notice that if a is repeated on forever that the exponent will equal the entire expression. So if a^a^a...=x, then a^x=x, so a=x^(1/x). If x is convergent then the function up to the convergent value will have unique outputted values. This is because a^a^a... will increase until it is divergent. If we find the maximum value of x^(1/x), then that will be the maximum value of x for a to be convergent. We can find the maximum by taking the derivative and setting it equal to 0. So y=x^(1/x), ln (y)= (ln x)/x--> (1/y) dy/dx=(1-ln x)/(ln x)^2-->dy/dx=(x^(1/x)) (1-ln x)/(ln x)^2, by the quotient rule. So (x^(1/x)) ((1-ln x)/(ln x)^2=0--> 1-ln x=0 (x^(1/x) and 1/(ln x)^2 can't equal 0)-->ln x=1-->x=e. So if that is the maximum, then the maximum value for a is e^(1/e) , which is approximately 1.444 .

Solve x=y^x, for y maximum and find x=e,

[Solve using WolframAlpha, d((1/x)log(x))/dx=0, solution x=e]

Therefore, e=y^e for maximum y

and we get y=e^(1/e)

Answer, y=1.4447