Trigonometry with Fractional Part? Too Much!
 {
x
}
(
{
x
}
−
1
)
(
tan
(
{
x
}
−
1
)
)
sin
{
x
}
{
x
}
(
{
x
}
−
1
)
(
tan
(
{
x
}
−
1
)
)
sin
{
x
}
What is the value of the above expression if we take for an arbitrary small value of x ? Which is to say, what is the limit of the said expression when x approaches 0 ?
Details and assumptions :
-
{ A } denote the fractional part of A . For example, A = 1 . 7 4 ⇒ { A } = 0 . 7 4 , B = − 1 . 3 ⇒ { B } = 0 . 7
-
{ x } = x − ⌊ x ⌋
To try more such problems click here .
Image Credit: Wikipedia Fraction
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions

Sorry to be catchy, but {B} = 0.7 in the question.
Log in to reply
No i suppose you got it wrong fraction part of
-1.3
i.e.,
{-1.3}
is indeed
-0.3
. Just look at the below graph of fractional part function.
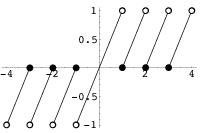
Log in to reply
fractional part is x − ⌊ x ⌋ = − 1 . 3 − ⌊ − 1 . 3 ⌋ = − 1 . 3 + 2 = 0 . 7
Also fractional part is never negative
Log in to reply
@Vighnesh Raut – Yes it withstands when x is +ve . Please view this,
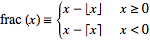
Did you understand?
Log in to reply
@Harshvardhan Mehta – no, the definition for fractional part is same whether it is positive or negative number . Check here
Log in to reply
@Vighnesh Raut – when x is +ve Floor function is considered but when x is -ve Ceiling function is considered. You can also Google regarding this. Or @Sandeep Bhardwaj sir can you help us out...
Log in to reply
@Harshvardhan Mehta – The wikipedia page that Vighnesh Raut linked gives both definitions. @Harshvardhan Mehta .
A function can be defined to do anything. Saying that there is exactly one definition is fallacious. Usually there is no problem since only one definition is used commonly. Since there is a problem here with some people using one definition and others using a different one, it would be best if you put the way you define the fractional part function under the details and assumptions.
Log in to reply
@Siddhartha Srivastava – Its Vighnesh Raut not Gupta...lol
Log in to reply
@Ram Kapoor – I don't know how or why I did that. xD Edited
Log in to reply
@Siddhartha Srivastava – happens...but I think that fractional part is positive ...
@Siddhartha Srivastava – So in the end whats the conclusion?? shall i remove the assumptions part or let it be.
Log in to reply
@Harshvardhan Mehta – Put your definition (The photo with which you replied to Darshak Mehta and Vignesh Raut) in the Details.
@Harshvardhan Mehta – Its not that -0.3 is wrong but we usually write fractional part as positive. Consider the remainder when 5 is divided by 7. Both -2 and 5 are answer to the problem but we usually use 5 as the answer..
Log in to reply
@Vighnesh Raut – I don't agree with this, saying { − 1 . 3 } = − 0 . 3 is completely wrong, because fractional part function has a definition that { x } = x − ⌊ x ⌋ and it is invalid according to this definition.
And when 5 is divided by 7 , 5 is called least positive remainder ( generally considered as remainder itself) and − 2 will be taken as least absolute remainder here. So generally, when we talk of remainder, we mean to say is least positive remainder. @Vighnesh Raut
Log in to reply
@Sandeep Bhardwaj – ok...Thanks for your help sir..It helped me a lot in clearing my doubts..
@Harshvardhan Mehta – No, @Harshvardhan Mehta you're not right at this point. Fractional part has always the same defination i.e. { x } = x − ⌊ x ⌋ . And fractional part is never negative. And { − 1 . 3 } = 0 . 7 , not − 0 . 3 . @Vighnesh Raut is right. I'm editing the problem accordingly. Thanks !
Log in to reply
@Sandeep Bhardwaj – well thanks for it and actually some moderator had put up the Assumptions part and yeah when asked the same thing on Wolfram Alpha it said its -0.3 can you explain why is it so?
Log in to reply
@Harshvardhan Mehta – It is so because you've given some other definition of fractional part here which is not correct. It will be − 0 . 3 according to your definition, but that's not the exact definition of fractional part function.
Log in to reply
@Sandeep Bhardwaj – Ohk thanks Sir.. maybe I made a wrong assumption regarding it. And yeah on further research just got to know that the definition I gave, its use was stopped quite some time back.. got to know from this link
Log in to reply
@Harshvardhan Mehta – hmmm fine. BTW you solution is nice. Great, keep it up!
@Harshvardhan Mehta – Where did you read that "it's use was stopped some time back"?
The link you've given clearly states that "Unfortunately, there is no universal agreement of the definition of frac ( x ) for x < 0 ." Even the Mathematica command uses the definition you gave.
I think that Vighnesh Raut's statement is correct . The range of fractional part is[0,1).& -0.3 do not lie in it. Please correct me if I am wrong.
Log in to reply
@Darshak Mehta – Yes it withstands when x is +ve . Also view this,
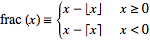
x = -0.0001 for f(x) = 0.841501103285097+
x = 0.0001 for f(x) =1.55722094561212+
Not the same range and therefore the limit tends to 0 does not exist.