This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Very nice and simple solution!
Doesn't your solution presuppose x can't be 1?
Log in to reply
Yeh, but we are not evaluating at x=1 we are taking the limit, which means that x is "almost" 1.
Using L'Hôpital's Rule ,
x → 1 lim x 1 0 − 1 x 1 5 − 1 = x → 1 lim 1 0 x 9 1 5 x 1 4 = 1 0 1 5 = 1 . 5
Moderator note:
Simple standard approach.
One should remember to (demonstrate that they) check we have an indeterminate form before applying L'hopital.
You could always include a link for these rules in your solution for the viewers. Anyway, nice solution. Upvoted.
I will give a complicated solution! The numerator is the product of all cyclotomic polynomials which divide 15 and the denominator is all cyclotomic polynomias F d where d divides 10. So we get F 2 F 1 0 F 3 F 1 5 . But F p ( 1 ) = p if p is prime and 1 otherwise. So we get 2 3 .
I loved this solution! (+1)
Can you explain in full?
Log in to reply
When you have a non-determinated form like "0/0" you can derive numerator and denominator the limit will remain the same. This is De l'Hopital rule.
Log in to reply
So for this particular problem as x-->0, L'Hôpital's rule would not apply because there is no indeterminate form?
Log in to reply
@Scott Morris – That's correct. The limit as x --> 0 would evalute to -1/-1 or just 1. If you applied L'Hopitals rule your answer would be zero, which is incorrect.
Log in to reply
@Ahern Nelson – Thanks, Ahern Nelson
Log in to reply
@Scott Morris – Sorry I disagree when X->1 the limit goes to a 0/0 form than I can apply de l'Hopital
Log in to reply
@Angelo De Luca – Are we talking about the sa e exercise? No doubt for me
Log in to reply
@Angelo De Luca – The limit si for X->1 and the function is (x^15-1)/(x^10-1) than (1-1)/(1-1) = 0/0 indeterminate form therefore You can apply de l'Hopital
L'Hopital's rule will help in solving this question..
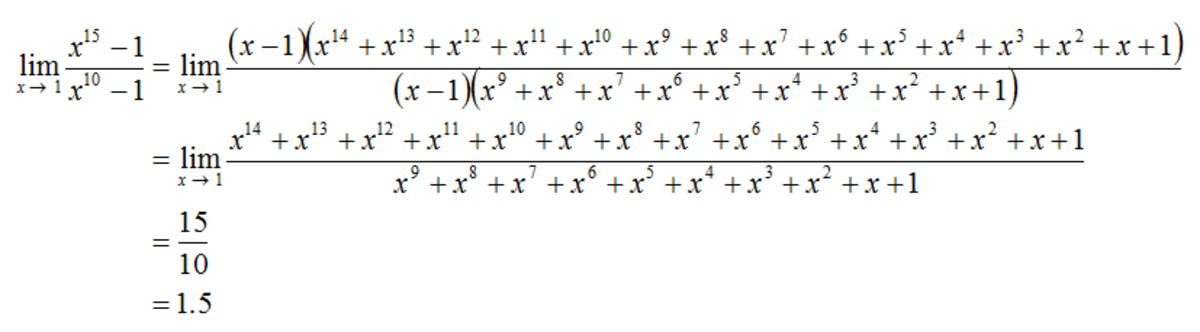
Substituting a = x 5 we have
x 1 0 − 1 x 1 5 − 1 = a 2 − 1 a 3 − 1 = ( a + 1 ) ( a − 1 ) ( a − 1 ) ( a 2 + a + 1 ) = a + 1 a 2 + a + 1
So
x → 1 lim x 1 0 − 1 x 1 5 − 1 = x → 1 lim x 5 + 1 x 1 0 + x 5 + 1 = 2 3