Limit, Sum, Fraction

Let the limit equals $A$

$\begin{aligned} \displaystyle\lim_{n\to\infty}\frac{\displaystyle\sum_{k=1}^{n}n^k}{n^n}&=\lim_{n\to\infty}\frac{n+n^2+n^3+n^4+\cdots+n^n}{n^n} \\ &=\displaystyle\lim_{n\to\infty}\left(1+\frac1n+\frac1{n^2}+\frac1{n^3}+\cdots+\frac1{n^{n-1}}\right)=1\\ \end{aligned}$

$\begin{aligned} A&=\displaystyle\lim_{n\to\infty}\frac{\displaystyle\sum_{k=1}^{n}n^k}{\displaystyle\sum_{k=1}^{n}k^n} \\ &=\displaystyle\lim_{n\to\infty}\frac{n^n}{\displaystyle\sum_{k=1}^{n}k^n} \\ \end{aligned}$

$\begin{aligned} \dfrac1A&=\displaystyle\lim_{n\to\infty}\frac{\displaystyle\sum_{k=1}^{n}k^n}{n^n}\\ &=\displaystyle\lim_{n\to\infty}\frac{1^n+2^n+3^n+4^n+\cdots+n^n}{n^n}\\ &=\displaystyle\lim_{n\to\infty}\left(1+(\frac{n-1}n)^n+(\frac{n-2}n)^n+(\frac{n-3}n)^n+\cdots\right)\\ &=\displaystyle1+\frac1e+\frac1{e^2}+\frac1{e^3}+\cdots=\frac{e}{e-1},A=\boxed{\frac{e-1}{e}}\\ \end{aligned}$

We need a little care with the convergence, here. Certainly $N(n) \; = \; \sum_{j=1}^n n^j \; = \; \frac{n(n^n-1)}{n-1}$ and hence $\lim_{n \to \infty}n^{-n}N(n) \; = \; \lim_{n \to \infty} \frac{n}{n-1}\big(1 - n^{-n}\big) \; =\; 1$ On the other hand, we have $D(n) \; = \; \sum_{j=1}^n j^n \; = \; \sum_{j=0}^{n-1}(n-j)^n$ so that $n^{-n}D(n) \; = \; \sum_{j=0}^{n-1} \big(1 - \tfrac{j}{n}\big)^n$ We have to be a little careful about letting $n$ tend to infinity both in the argument $\big(1 - \tfrac{j}{n}\big)^n$ and as a limit of the sum simultaneously. Since $\frac{d}{dx}\big[(n+1)\ln(1 - \tfrac{x}{n+1}\big) - n\ln\big(1 - \tfrac{x}{n}\big)\big] \; = \; \frac{x}{(n-x)(n+1-x)} \; > \; 0 \hspace{2cm} 0 < x < n$ we deduce that $\big(1 - \tfrac{x}{n}\big)^n < \big(1 - \tfrac{x}{n+1}\big)^{n+1}$ for $0 < x < n$ , and hence $\big(1 - \tfrac{x}{n}\big)^n$ (for $n > x$ ) converges to $e^{-x}$ in a monotonic increasing manner. Thus we deduce that $n^{-n}D(n)$ is an increasing sequence, and that $n^{-n}D(n) \; = \; \sum_{j=0}^{n-1} \big(1 - \tfrac{j}{n}\big)^n \; \le \; \sum_{j=0}^{n-1} e^{-j} \; < \; \sum_{j=0}^\infty e^{-j} \; = \; \frac{1}{1 - e^{-1}} \; = \; \frac{e}{e-1}$ for all $n$ . In particular, this implies that $\lim_{n \to \infty}n^{-n}D(n)$ exists. Now, $n^{-n}D(n) \; \ge \sum_{j=0}^{N-1} \big(1 - \tfrac{j}{n}\big)^n \hspace{2cm} n \ge N$ for any positive integer $N$ , and hence (letting $n \to \infty$ ) $\tfrac{e}{e-1} \; \ge \; \lim_{n \to \infty} n^{-n}D(n) \; \ge \; \sum_{j=0}^{N-1} e^{-j}$ for any positive integer $N$ . Now we can let $N \to \infty$ to deduce that $\lim_{n\to\infty}n^{-n}D(n) \,= \, \tfrac{e}{e-1}$ . Thus $\lim_{n \to \infty} \frac{N(n)}{D(n)} \; = \; \lim_{n\to \infty} \frac{n^{-n}N(n)}{n^{-n}D(n)} \; = \; \frac{e-1}{e} \; = \; \boxed{0.6321205588}$

Relevant wiki: Bernoulli numbers

In the following solution, $B_n$ represent the Bernoulli numbers.

$\displaystyle A=\lim _{ n\rightarrow \infty }{ \frac { n+{ n }^{ 2 }+...+{ n }^{ n } }{ 1+{ 2 }^{ n }+...+{ n }^{ n } } }$

$\displaystyle =\lim _{ n\rightarrow \infty }{ \frac { \frac { { n }^{ n+1 }-n }{ n-1 } }{ \frac { { n }^{ n+1 } }{ n+1 } +\frac { { n }^{ n } }{ 2 } +{n \choose 1}\frac { B_{ 2 } }{ 2 } { n }^{ n-1 }+{n \choose 3}\frac { B_{ 4 } }{ 4 } { n }^{ n-3 }+... } }$

$\displaystyle =\lim _{ n\rightarrow \infty }{ \frac { { n }^{ n+1 }-n }{ \frac { n-1 }{ n+1 } { n }^{ n+1 }+\frac { n-1 }{ 2 } { n }^{ n }+ (n-1){n \choose 1}\frac { B_{ 2 } }{ 2 } { n }^{ n-1 }+(n-1){n \choose 3}\frac { B_{ 4 } }{ 4 } { n }^{ n-3 }+... } }$

(ignoring all ${ n }^{ n }$ , ${ n }^{ n-1 }$ , ${ n }^{ n-2 }$ …)

$\displaystyle =\frac { 1 }{ 1+\frac { 1 }{ 2 } +\frac { 1 }{ 1! } \frac { B_{ 2 } }{ 2 } +\frac { 1 }{ 3! } \frac { B_{ 4 } }{ 4 } +... }$

$\displaystyle =\frac { 1 }{\displaystyle \sum _{ k=0 }^{ \infty }{ \frac { B_{ k } }{ k! } +1 } }$ (with $B_0=1$ , $B_1=-\frac {1}{2}$ , $B_3=B_5=B_7=...=0$ )

On the other hand, we have $\displaystyle f(x)=\frac { x }{ { e }^{ x }-1 } = \displaystyle \sum _{ k=0 }^{ \infty }{ B_{ k } } \frac { { x }^{ k } }{ k! }$ , so

$\displaystyle A=\frac { 1 }{\displaystyle \sum _{ k=0 }^{ \infty }{ \frac { B_{ k } }{ k! } +1 } } = \frac { 1 }{ f(1)+1} = \frac { e-1 }{e} = 1-\frac {1}{e}$

$\begin{aligned}&\lim_{n \to \infty}\dfrac{n + n^2 + n^3 + \cdots + n^{n}}{1^{n} + 2^{n} + 3^{n} + \cdots + n^{n}} = \\ &\lim_{n \to \infty}\dfrac{n^{n}\left ( 1 + \frac{1}{n} + \frac{1}{n^{2}} + \frac{1}{n^3} + \cdots + \frac{1}{n^{n-1}}\right )}{n^{n}\left (1 + \left ( \frac{n-1}{n}\right)^{n} + \left ( \frac{n-2}{n} \right )^{n} + \left ( \frac{n-3}{n} \right )^{n} + \cdots + \left ( \frac{n-(n-1)}{n} \right )^{n}\right )} = \\ &\lim_{n \to \infty}\dfrac{\sum_{k = 0}^{n-1}\left ( \frac{1}{n}\right)^{k}}{\sum_{k = 0}^{n-1}\left (1 - \frac{k}{n}\right)^{n}} = \\ &\dfrac{1}{\sum_{k = 0}^{\infty}e^{-k}} = \dfrac{1}{\frac{1}{1 - e^{-1}}} = 1-e^{-1} \approx 0.63212\end{aligned}$

$n^n - 1 = (n - 1)(n^{n - 1} + n^{n - 2} + ... + 1) \implies n^{n - 1} + n^{n - 2} + ... + 1 = \dfrac{n^n - 1}{n - 1} \implies \sum_{p = 1}^{n} n^p = \dfrac{n(n^n - 1)}{n - 1}$

Dividing numerator and denominator by $n^n \implies \displaystyle \lim_{n\to\infty} \dfrac{n + n^2+ n^3 + \cdots + n^n}{1^n + 2^n + 3^n + \cdots + n^n} =$ $\lim_{n \rightarrow \infty} \dfrac{(1 - \dfrac{1}{n^n})(1 + \dfrac{1}{n - 1})}{\sum_{j = 0}^{n - 1} (1 -\dfrac{j}{n})^n} =$ $\dfrac{1}{\sum_{n = 0}^{\infty} (\dfrac{1}{e})^n} = \dfrac{1}{\dfrac{1}{1 - \dfrac{1}{e}}} = \dfrac{e - 1}{e} \approx \boxed{0.63212}$

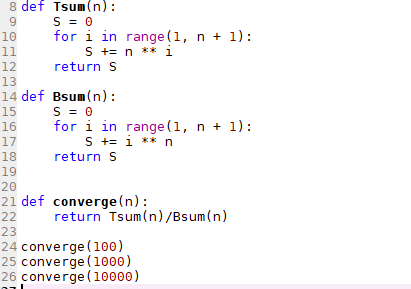
Obviously only for verification purposes.