Line, Circle or a Cross?
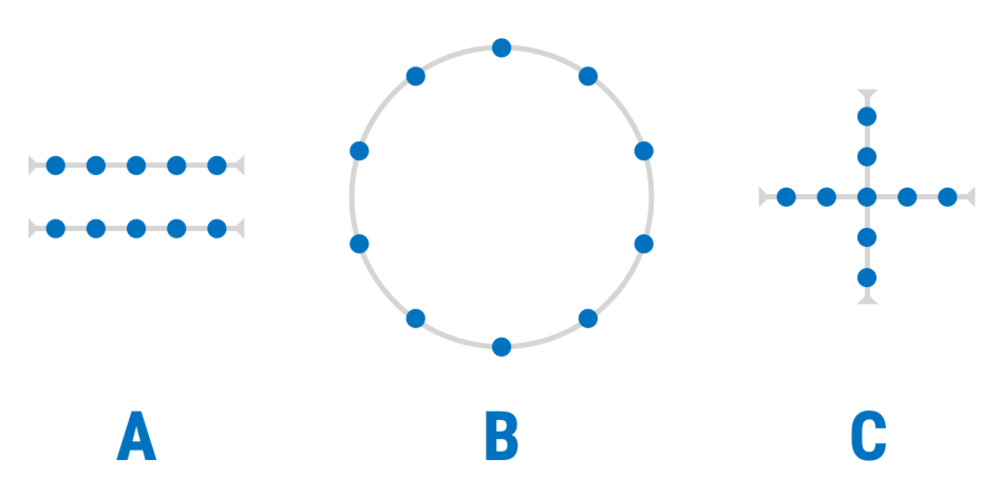
If each vertex of a non-degenerate triangle is one of these dots, which arrangement forms the most non-degenerate triangles?
- Arrangement A: Points on two parallel lines
- Arrangement B: Points on a circle
- Arrangement C: Points on a two intersecting lines
Note:
- Here, a non-degenerate means that the vertices of the triangle must be three different dots, and those three dots cannot all be on the same straight line.
- The question asks which arrangement has the most number of triangles
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thanks for introducing both aspects. Also, we can calculate the possibilities of A the same as we did for C.
( 3 1 0 ) − ( 3 5 ) − ( 3 5 ) = 1 0 0
Log in to reply
Ah, yes, I meant to mention that! Thanks for pointing out.
There is no restriction for choosing the three dots in circle, hence it can form the most non-degenerate triangles.
Ah, I thought it was the figure with the most degenerate triangles.
Any three points of the B shape are not collinear (no matter how many points there are on the circle), so it can form the most non-degenerate triangles.
Log in to reply
Oh, is the wording a bit confusing?
"Any three points of the B shape are not collinear (no matter how many points there are on the circle), so it can form the most non-degenerate triangles."
And your reasoning is correct, similar to Pop Wong's
Log in to reply
I think he supposed the options of choice are in sequence A, B and C.
In graphic B, any three points will not connect to form a line :)
The sentence in brackets is an extended thinking about the B shape: no matter how many points there are on the circle, any three points will not be connected in a straight line.
Log in to reply
@Zhiqian Chen – Sorry if you misunderstood my comment, I meant "is the wording for the question a bit confusing" since you thought the question asked "figure with the most degenerate triangles". I wasn't confused by your explanation
Log in to reply
@Mahdi Raza – No, no, there is no problem with your topic, I read it wrong :D
Figure A has 5 dots each in both the lines. To form a non-degenerate triangle, we could either have the 2 dots on the first line and the remaining dot on the second line or vice versa. So choosing 2 dots from any line first is basically choosing 2 objects from 5 objects in no order i.e 5 C 2 = 1 0 and then we could choose 1 dot out of the 5 from the other line, so total triangles is 1 0 × 5 = 5 0 but as there are 2 lines, we could do first with the up line and then with down so there are twice more triangles actually. Thus arrangement A can form 5 0 × 2 = 1 0 0 triangles.
For figure B as all points are not colinear, we choose any 3 points with no order which is choosing 3 dots out of the total 10 dots, i.e 1 0 C 3 = 1 2 0 total triangles.
For figure C, the figure has the same no. of dots in the vertical and horizontal line, if we exclude the middle dot, we could first choose the 2 dots from the horizontal line i.e out of 4 dots which is 4 C 2 = 6 and then we could choose the remaining 1 out of the 4 in the vertical line, so there are total 6 × 4 = 2 4 triangles, however we could take the 2 dots from the vertical line and then the remaining from the horizontal so there are twice as much, 2 4 × 2 = 4 8 triangles. Now our first dot could be the middle one, and we could choose any 1 out of the 4 from the vertical line and one out of the 4 from the horizontal line, so 4 × 4 = 1 6 triangles. So total triangles = 16+48=64.
As 120>100>64, Arrangement B can form the most triangles.
240 -> 120.
Thanks for the elaborate answer, I believe you have a mistake for the number of triangles in B. Although answer is correct the number is not right
( 3 1 0 ) = 1 2 0
Quick answer: any three of the ten points in arrangement B form a triangle (there are ( 3 1 0 ) of these).
There are also ten points in arrangement A, but this time some choices of three points don't form a triangle.
In arrangement C, there are just nine points, and not every choice of three works, so there are definitely fewer triangles.
So arrangement B has the most triangles.
Slow answer: to make a triangle in arrangement A, we need two points in one row and one in the other. We get a total of 2 ⋅ ( 2 5 ) ⋅ ( 1 5 ) = 1 0 0 different triangles.
In arrangement B, as above, there are ( 3 1 0 ) = 1 2 0
In arrangement C, there are a total of ( 3 9 ) = 8 4 ways to choose three points. But ( 3 5 ) = 1 0 of these lie on the vertical line, and another 1 0 on the horizontal. So there are ( 3 9 ) − 2 ⋅ ( 3 5 ) = 6 4 triangles in arrangement C.