Line from nowhere

Extend PQ and BC such that they intersect at E .

Apply Menelaus Theorem .

Result => CE = 2BE or

B is midpoint of CE .

By congruency , angle BQC = angle BQE = angle AQP

You will get Theta = 36

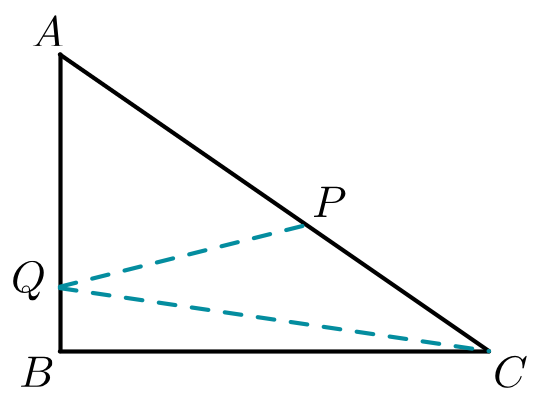Let $\theta = \angle PQC$ . Then $\angle AQP = 2 \theta$ and $\angle BQC = 180^{\circ} - 3 \theta$ .

"Line from nowhere"

Now let $a = BC$ and let $c = AB$ . Draw a perpendicular from $P$ to $AB$ so that it meets $AB$ at $D$ . Then $PD \perp AB$ and $PD \parallel BC$ . Therefore $\triangle APD$ is similar to $\triangle ACB$ by a factor of $\frac{3}{5}$ (because $\frac{AP}{AC} = \frac{3}{5}$ ). Thus $DP = \frac{3}{5} a$ and $AD = \frac{3}{5} c$ . Thus $DB = \frac{2}{5} c$ . Furthermore, since $AQ = 3QB$ , then $QB = \frac{c}{4}$ and $AQ = \frac{3c}{4}$ . Hence, $DQ = DB - QB = \frac{2}{5} c - \frac{c}{4} = \frac{3}{20} c$ Therefore,, in $\triangle DQP$ we have: $tan(2\theta) = \frac{PD}{DQ} = \frac{3a/5}{3c/20} = \frac{4a}{c}$ Similarly, in $\triangle BQC$ , we hve: $tan(\angle BQC) = tan(180^{\circ} - 3 \theta) = \frac{BC}{QB} = \frac{a}{c/4} = \frac{4a}{c}$

Hence, $tan(2\theta) = tan(180^{\circ} - 3 \theta)$ . Since both of these angles are strictly between $0$ and $180^{\circ}$ , then they must be equal. Hence, $2\theta = 180^{\circ} - 3 \theta$ $5\theta = 180^{\circ}$ $\theta = \boxed{36^{\circ}}$

choose M is midpoint of PC, => PQ // BM => PQA angle = QBM angle BM intersects QC at K => K is midpoint of QC Because BQC is a right triangle => QBM angle = BQC angle => 5 PQC angle = 180 degree => PQC angle = 36 degree

[AQP] means angle AQP. On ray AB, denote K such that:BQ=BK. Hence: AQ/QK=3/2 => AQ/QK=AP/PC => QP is parallel to KC. Thus, [AQP]=[BKC]. On the other hand: [BKC]= BQC . So, [AQP]=[BQC]=2[PQC]. We have: [AQP]+[PQC]+[BQC]=180 => 2[PQC]+[PQC]+2[PQC]=180 => [PQC]=36. 36 is the correct answer.

K is PQ x CD, call H in the line CD that is orthogonal with line BC and satisfies: $QH \perp CD, CD \perp BC \Rightarrow \frac{KC}{QA}=\frac{CP}{PA}=\frac{2}{3}$ ABCD is a rectangular, because: $\frac{QA}{AB}=\frac{3}{4} \Rightarrow KC=\frac{3}{4} \times \frac{2}{3} \times AB=\frac{AB}{2}$ $QB=\frac{AB}{4} \Rightarrow HC=QB=\frac{KC}{2}$ $\Rightarrow KQ=QC, \angle{KQH}=\angle{HQC}=\frac{\angle{PQC}}{2}$ $\Rightarrow \angle{HQC}=\frac{HQA}{5}=18^{o} \Rightarrow \angle{PQC}=\boxed{36^{o}}$