Link’s Color Puzzle
In Nintendo's Link's Awakening's Color Dungeon, Link enters a room with a 3 × 3 checkerboard pattern of blue and red balls. When Link hits one of the balls with his sword, that ball and any ball immediately above, below, left, and right of it all toggle between blue and red. To pass to the next room, Link must change all the balls to blue, which is possible by hitting just 4 balls:

If Link enters a room with the same set of rules but with a 5 × 5 checkerboard pattern of blue and red balls instead, what is the minimum number of balls Link needs to hit in order to pass to the next room?

Note: A computer program will probably be needed to solve this problem.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
OK, I've already answered one of my own questions: we don't need Cramer's rule, we can directly solve by inverting M . This will in general give a matrix with non-integer values; but if we multiply this by det M we get back to integers, which we can reduce modulo 2 to give the inverse we need.
Wow, nice work! (Sorry I don't have any answers for you, though.)
We need to hit the balls on the positions: ((0, 0), (0, 1), (0, 2), (2, 1), (2, 4), (3, 0), (3, 2), (3, 4), (4, 1), (4, 4)). Above sequence is also the shortest possible. Observe, that the order of hits does not matter.
It seems, that such problems all well known and that they are efficiently solved using some linear algebra (linear spaces over the field Z 2 ). The game is called "Lights out". Cf. Marlow Anderson, Todd Feil (1998). "Turning Lights Out with Linear Algebra" . Mathematics Magazine. 71 (4): 300–303.
Besides that, I have written the following script to obtain a solution. It iterates through all of the possible hit lists (up to rotations/reflections/order of hits). It is a parallel code. But it is not really useful for bigger grids.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 |
|
Same solution (and same technique). Up to rotations/reflections, this was the only solution I found - did you find any others?
Log in to reply
I also used a computer program to prove that the minimum is 10, and only found this solution (along with its rotations/reflections).
Log in to reply
Did you try any analytical methods? It seems unlikely that an analytical method could generate the solution, but perhaps it could rule out solutions with fewer steps. There are lots of other questions here...is it always possible to solve this puzzle on an n × n grid? If not, which n work? Is the solution always unique?
Log in to reply
@Chris Lewis – Before, I thought that (sorry, I do not know, how to cross it out): "I think, that there is no solution when n is even." Above is not true.
It turned out, that there is a solution for 6 and 8. I have found the following solutions (I am not sure, if they are the only ones up to rotations/reflections neither the shortest possible).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
|
Log in to reply
@Piotr Idzik – Is there a solution for all odd n ? (Another question is, how many hits are needed?)
Log in to reply
@Chris Lewis – It turned out, that there is a solution for 6 and 8 (cf. my comment above)
@Chris Lewis – There's also 2 hits minimum required for a 2 x 2 board (hit the two original red balls)
So in summary (so far):
| gridsize | minimum hits required |
| 2 x 2 | 2 |
| 3 x 3 | 4 |
| 4 x 4 | not possible |
| 5 x 5 | 10 |
| 6 x 6 | 22 |
| 7 x 7 | 16 |
| 8 x 8 | 36 |
I also noticed that for odd gridsize solutions, a previous odd gridsize solution is in the corner. (For example, the 3 x 3 solution is in the corner of the 5 x 5 solution.) I wonder if the coding can be improved with this recursive relation in mind, in other words, for an odd n x n solution, start with a known (n - 2) x (n - 2) solution in the top left corner and only try all possible combinations of the balls in the remaining L-shape. Unfortunately this recursive relation does not seem to be true for even gridsize solutions, though.
Log in to reply
@David Vreken – It seems that OEIS does not know about the sequence 10, 22, 16, 36.
@David Vreken – Update: I wrote a computer program that uses a recursive relation, but unfortunately it was not very efficient (I could only prove up to a 7 x 7 grid, the 8 x 8 would grid take too long to calculate). I can verify that the solutions already found above are the only solutions for those gridsizes, except the 5 x 5 solution has 4 solutions (all rotations/reflections). Basically, the program stores all possible ways to get all blue in the top left (n - 1) x (n - 1) corner, and then uses those to test the n x n gridsize.
@David Vreken – Here is the computer program I wrote:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 |
|
@David Vreken – and its output:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
|
@David Vreken – Here is a solution I found manually for a 9 x 9 grid that uses 44 hits. I'm not sure if it's a minimum, though.
1 2 3 4 5 6 7 8 9 |
|
@David Vreken – Here is another solution I found manually for a 9 x 9 grid that uses only 28 hits. I'm still not sure if it's a minimum, though.
1 2 3 4 5 6 7 8 9 |
|
@David Vreken – In fact, this pattern can be used to show that there exists at least one solution for any odd n × n gridsize for n ≥ 3 :

Let c be the number of 3 × 3 checkerboard sections going across the grid, let b be the number of 1 × 3 bars going across the grid, and let g be the number of 1 square gaps going across the grid (between checkerboard sections and the bar sections). Then n = 3 c + b + g . Now g is one less than the total number of checkerboard and bar sections, so g = b + c − 1 , which means n = 4 c + 2 b − 1 .
There are three different cases to consider:
(1) The number of checkerboards sections is the same as the number of bar sections. Then b = c so that n = 4 c + 2 c − 1 = 6 c − 1 .
(2) The number of checkerboards sections is one more than the number of bar sections. Then b = c + 1 so that n = 4 c + 2 ( c + 1 ) − 1 = 6 c + 1 .
(3) The number of checkerboards sections is one less than the number of bar sections. Then b = c − 1 so that n = 4 c + 2 ( c − 1 ) − 1 = 6 c − 3 .
Since 6 c − 1 , 6 c + 1 , and 6 c − 3 cover all the odd numbers greater than 3 , there is at least one solution for any odd n × n gridsize for n ≥ 3 using the above pattern.
Using the above pattern, the number of hits h is
h = 1 8 1 ( 5 n + 1 3 ) ( n − 1 ) if n is in the form 6 k + 1
h = 1 8 1 ( 5 n − 3 ) ( n + 3 ) if n is in the form 6 k + 3
h = 1 8 5 ( n + 1 ) 2 if n is in the form 6 k − 1
Do you mean this solution is the only one you found using 10 moves? Or that it is the only solution you found at all?
Log in to reply
@Matthew Feig – I meant the first, but later on I found that both are true. Just to clarify, there are four different ways, but all rotations/reflections of one way:
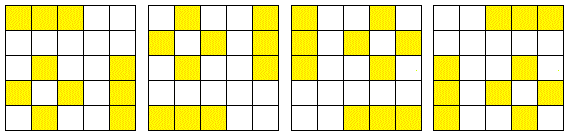
and these are the only ways to solve the puzzle at all (without hitting an individual ball more than once)
idk i just guess and got it right because i played that game on nintedo , so i know that
I got this right by just estimating in my head.
I pretty much did the same thing. 👍🏻
I've just seen that this approach is not original ( @Piotr Idzik references a paper on it) but thought it might be interesting to add a different method to the discussion.
We'll work on the general n × n case, then look at a specific example.
Code the lights by their colour: use 1 for blue lights and 0 for red. Toggling a light's colour is equivalent to adding 1 to its value, working modulo 2 .
Define a "hit matrix" H by H i j = 1 if the light in position ( i , j ) is hit, and 0 otherwise. Define the starting checkerboard pattern as C , where C i j ≡ i + j + 1 ( m o d 2 ) . We can also define the final, all blue setup as B with all entries equal to 1 .
The final colour of the light in position ( i , j ) is given by C i j + H i j + H i − 1 , j + H i , j + 1 + H i + 1 , j + H i , j − 1 , where we ignore indices outside the range [ 1 , n ] . We want this to be congruent to 1 ( m o d 2 ) for all ( i , j ) .
The idea is to solve a linear equation in H to find a hit matrix that works. However, to do this, we need (I think) to rewrite the entries of H as a column vector, H v = ( H 1 1 , H 1 2 , … , H 1 n , H 2 1 , … , H n n ) T . Because this column vector has n 2 entries, I'll discuss the 3 × 3 case first.
Let's start writing equations modulo 2 . The first row of lights give:
1 + H 1 1 + H 1 2 + H 2 1 0 + H 1 1 + H 1 2 + H 1 3 + H 2 2 1 + H 1 2 + H 1 3 + H 2 3 ≡ 1 ≡ 1 ≡ 1
Continuing this way, we get the following equation:
⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 1 0 1 0 0 0 0 0 1 1 1 0 1 0 0 0 0 0 1 1 0 0 1 0 0 0 1 0 0 1 1 0 1 0 0 0 1 0 1 1 1 0 1 0 0 0 1 0 1 1 0 0 1 0 0 0 1 0 0 1 1 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 1 0 1 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ H v = M ⋅ H v ≡ B − C
This looks daunting, but is linear. The determinant of M is odd, which means it has an inverse modulo 2 . This means there is a unique solution to the equation!
We can solve the equation using Cramer's rule ; as expected, the final result is
H = ⎝ ⎛ 0 1 0 1 0 1 0 1 0 ⎠ ⎞
Now, of course, this result in itself just repeats the animation in the question. But we get the following useful information:
any size grid can be encoded in this way; the pattern of the coefficient matrix M continues in the obvious way
if the determinant of M is odd, there is a unique solution (so there is no question of the minimum number of hits, or even of the pattern)
if the determinant of M is odd, we can use Cramer's rule to directly generate the solution
Now let's turn to the 5 × 5 case of the question. We can set all the matrices and H v up in exactly the same way. And what do we find for det M ?
It is, of course, even.
But this just means there is not a unique solution. If we reduce the matrix by removing the first two rows and first two columns, we get a matrix M ′ whose determinant is odd.
This matrix reduction means we have some freedom of choice; we can choose which of the first two lights (in positions ( 1 , 1 ) and ( 1 , 2 ) ) are hit - in other words, there are four solutions. But this is exactly what we expect! As shown in the other solutions, the winning matrix is
H = ⎝ ⎜ ⎜ ⎜ ⎜ ⎛ 1 0 0 1 0 1 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎞
and its rotations. Each of the four rotations corresponds to a choice of which of the first two lights are hit.
So, without needing to analyse the 2 2 5 different hit matrices, we have shown there is a unique solution with 1 0 hits, up to rotation.
Some questions I have about this approach:
is there a better method for solving the equations than Cramer's rule? If it's possible to compute M − 1 easily, that would make the calculation much quicker
how many degrees of freedom are there for each n ? (ie, how many hits do we have to choose before we get to a non-singular matrix?) If there are multiple valid configurations, is there a quick way to determine which ones minimise the total number of hits?
alternatively, which n - like n = 3 - have det M ≡ 1 ( m o d 2 ) (ie no degrees of freedom)?
is it possible to set up the equations so that we solve for H directly in its matrix form? (This seems to involve pre- and post-multiplying coefficient matrices; we essentially get an equation of the form A H + H A ≡ B − C , but I'm not sure how to solve these)