Load Power vs. Load Angle

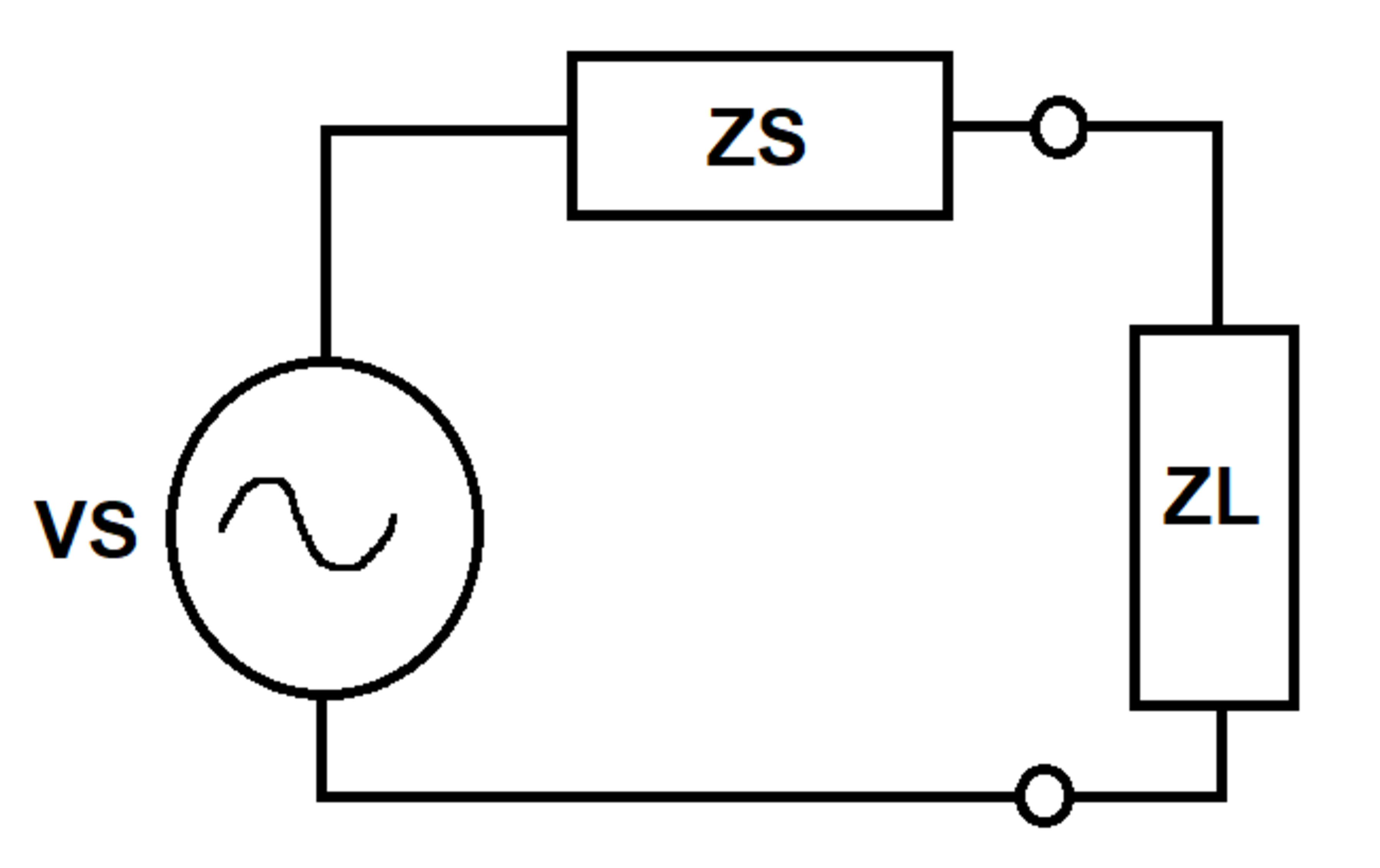
Electricity and Magnetism Level pending

An AC voltage source has internal voltage $V_S$ and internal impedance $Z_S$ . A load impedance $Z_L$ is connected across the source terminals. $Z_L$ has the following form:

$Z_L = \sqrt{5} \, e^{j \theta} \\ -\pi/2 \leq \theta \leq \pi/2$

The active power (in watts) dissipated by the load at a particular angle $\theta$ is $P_L (\theta)$ . Determine the following integral:

$\int_{-\pi/2}^{\pi/2} P_L(\theta) \, d \theta$

Bonus: Make a plot of $P_L$ vs. $\theta$ . Which $\theta$ value yields maximum $P_L$ , and what is notable about it?

Details and Assumptions:
1) $V_S = 10 + j 0$
2) $Z_S = 1 + j 2$
3) $j = \sqrt{-1}$
4) Source voltage is given in RMS (root mean square value)

The answer is 44.44.

1 solution

Karan Chatrath
Feb 21, 2021

Solution outline only provided.

$I = \frac{V_S}{Z_S+Z_L} \implies P_L = \mathrm{real}\left(IZ_LI^{*}\right)$

Plugging in the expressions and given values gives the required function $P_L(\theta)$ . Here, the angle is deliberately plotted in degrees. From this point, it is easy to numerically compute the required integral (it can probably be done analytically too, but I did not compute the exact integrand to be sure) . The required answer is: $\boxed{\int_{-\pi/2}^{\pi/2} P_L(\theta) \ d\theta \approx 44.44}$

The value of $\theta$ for which $P_L(\theta)$ is maximum is $\boxed{-63.432^{\circ}}$ . This happens to be the negative of the phase of the complex number $Z_S$ .

Solution edited slightly.

Karan Chatrath - 3 months, 2 weeks ago

I just read your comment to my solution to your previous problem. Now it makes sense. Thanks!

Karan Chatrath - 3 months, 2 weeks ago

That optimal angle corresponds to $Z_L = 1 - j 2$ , which is the complex conjugate of the source impedance.

Steven Chase - 3 months, 2 weeks ago

I am attempting your latest problem and I have wound up with a rather expensive optimization problem in 5 variables (the three real parts of impedances and the two imaginary parts). To solve this problem, I could honestly use a hint as to how to approach this in a time efficient manner.

Karan Chatrath - 3 months ago

Indeed, this one can be as hard as you want. The easy way is:

1) Calculate the currents from the reference case
2) Sweep the real part of ZA from zero to some upper bound (determined by RB and RC not allowed to be negative)
3) For each RA, take a voltage drop using the known current to calculate VN
4) Knowing VN and the required currents for IB and IC, calculate the impedances for ZB and ZC

Steven Chase - 3 months ago

Your suggestion is a really neat method. Unfortunately, I got the wrong answer. Could you give feedback? Hoping that my code is readable.

clear all
clc


VA     = 100;
VB     = 100*exp(-1i*2*pi/3);
VC     = 100*exp(1i*2*pi/3);

ZAo    = 1;
ZBo    = 2 + 1i*1;
ZCo    = 3 - 1i*2;

A      = [ZAo 0 0 1;...
    0 ZBo 0 1;0 0 ZCo 1;...
    1 1 1 0];

b      = [VA;VB;VC;0];

S      = inv(A)*b;

IA     = [1 0 0 0]*S;
IB     = [0 1 0 0]*S;
IC     = [0 0 1 0]*S;

dZ     = 1e-6;
V_min  = 99999;

for ZA = 0:dZ:100

    VN      = VA - IA*ZA;
    ZB      = (VB - VN)/IB;
    ZC      = (VC - VN)/IC;

    if abs(VN) < V_min && real(ZB) > 0 && real(ZC) > 0
        V_min = VN;
        Z_ans = real(ZA + ZB + ZC);
    end

end
ANSWER   = Z_ans
% ANSWER = 5.4105

Karan Chatrath - 3 months ago

@Karan Chatrath – Do your currents add to zero in the base case?

Steven Chase - 3 months ago

@Steven Chase – Yes, they do add to zero

Karan Chatrath - 3 months ago

@Karan Chatrath – Here are mine:

(76.6144161503+6.9101055907j)
(-45.2927204974-17.1998571452j)
(-31.3216956529+10.2897515545j)

Steven Chase - 3 months ago

@Steven Chase – I obtain the same.

Karan Chatrath - 3 months ago

@Karan Chatrath – Strange. I don't see any real difference. I have attached my code:

import math

a = complex(math.cos(2.0*math.pi/3.0),math.sin(2.0*math.pi/3.0))

VA = 100.0
VB = 100.0*(a**2.0)
VC = 100.0*a

ZA0 = complex(1.0,0.0)
ZB0 = complex(2.0,1.0)
ZC0 = complex(3.0,-2.0)

right = VA/ZA0 + VB/ZB0 + VC/ZC0
left = 1.0/ZA0 + 1.0/ZB0 + 1.0/ZC0

VN = right/left

IA = (VA-VN)/ZA0
IB = (VB-VN)/ZB0
IC = (VC-VN)/ZC0

print VA
print VB
print VC
print VN
print ""
print IA
print IB
print IC
print ""
print abs(IA + IB + IC)
print ""
print ""

#>>> 
#100.0
#(-50-86.6025403784j)
#(-50+86.6025403784j)
#(23.3855838497-6.9101055907j)

#(76.6144161503+6.9101055907j)
#(-45.2927204974-17.1998571452j)
#(-31.3216956529+10.2897515545j)

#3.5527136788e-15

#####################################################################

dRA = 10.0**(-6.0)

VNmin = 9999999999.0
Rtot_store = 0.0

#####################################################################

flag = 0

RA = 0.0

#print "RA Rtot VNmag"

while flag == 0:

    ZA = complex(RA,0.0)

    VN = VA - ZA*IA

    ZB = (VB-VN)/IB
    ZC = (VC-VN)/IC

    if ZB.real < 0.0:
        flag = 1

    if ZC.real < 0.0:
        flag = 1

    Rtot = ZA.real + ZB.real + ZC.real

    if abs(VN) < VNmin:

        VNmin = abs(VN)
        RA_store = RA
        Rtot_store = Rtot

    #print RA,Rtot,abs(VN)

    RA = RA + dRA

#####################################################################

print ""
print ""

print dRA
print RA
print RA_store
print ""
print Rtot_store
print VNmin

#1e-06
#2.30806099997
#1.29470499998

#5.21274201287
#8.98286510783
#>>>

Steven Chase - 3 months ago

@Karan Chatrath – Do you need to say Vmin = abs(VN)?

Steven Chase - 3 months ago

@Steven Chase – Nice catch. I just reran the code and I get the answer you obtained. Thank you for the feedback. Bummer that I could not get this one right. It was fun

Karan Chatrath - 3 months ago

@Karan Chatrath – I would delete and repost, but somebody has already solved

Steven Chase - 3 months ago

@Steven Chase – Oh it is okay. I would not expect you to repost anyway. I got it wrong fair and square. Plus I see this as a lesson in presence of mind. This tiny mistake was not easy to spot for me.

Karan Chatrath - 3 months ago

@Karan Chatrath – Alright, glad you enjoyed it despite the unfortunate luck

Steven Chase - 3 months ago

Load Power vs. Load Angle

The answer is 44.44.

1 solution

0 pending reports