Locus of the incenter of $\triangle ABC$

Considering the triangle $AIB$ we have $\frac{AI}{\sin(\frac14\pi - \theta)} \; = \; \frac{2}{\sin\tfrac34\pi}$ and hence $AI = 2(\cos\theta - \sin\theta)$ . Thus the coordinates of the incentre of $ABC$ are $\big( X \; = \; -1 + 2(\cos\theta - \sin\theta)\cos\theta\,,\,Y \; = \; 2(\cos\theta - \sin\theta)\sin\theta\big) \hspace{2cm} 0 \le \theta \le \tfrac14\pi$ at least for the top half of the locus, and so the desired area is $2\int_{\frac14\pi}^0 Y(\theta)\,X'(\theta)\,d\theta \; = \; \boxed{\pi-2}$

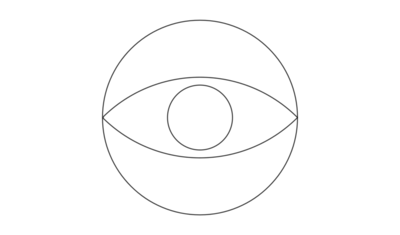
Indeed we see that $X \; = \; \cos2\theta - \sin2\theta \hspace{2cm} Y \; = \; \cos2\theta + \sin2\theta - 1$ and hence $X^2 + (Y+1)^2 = 2$ so the upper half of the locus lies on the circle with centre $(0,-1)$ and radius $\sqrt{2}$ . This means that the area contained in the locus is $2 \times \Big[\tfrac12 \times \sqrt{2}^2 \times \tfrac12\pi - \tfrac12 \times \sqrt{2}^2 \times \sin\tfrac12\pi\Big] \; = \; \pi - 2$