Logarithm-exponential Equation Conundrum
Ahmad was trying to find the number of solutions to
lo g ( 1 / 1 6 ) x = ( 1 6 1 ) x .
He noticed that these functions are inverses of each other. He drew a sketch of the function y = lo g ( 1 / 1 6 ) x in red, and then flipped it about the line y = x (shown in dotted green), to obtain a sketch of the function y = ( 1 6 1 ) x in blue.
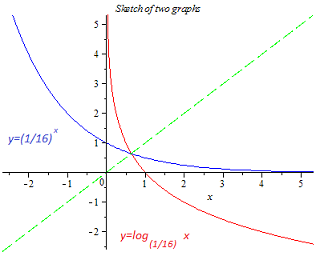
The picture suggests that the equation has one real solution. But algebra suggests that there are two: x = 4 1 and x = 2 1 . How many real solutions does this equation actually have?
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great solution. Are the graphs shown are wrong then?
Log in to reply
Yes, the graph in the problem is misleading. The graph in the solution gives a more accurate localized view of what's happening about that point of intersection.
Log in to reply
It is always the right way in such a case drawing the difference of the functions to determine the roots.
Log in to reply
@Andreas Wendler – That is one possible approach. However, it might not be easy for you to accurately draw the graph to understand how it looks like. (Yes, we can use graphing software to see the graph, and zoom in on the action about the line y = 0 .)
Solution is also wrong🤣
Log in to reply
What do you think is wrong with the solution?
The word "sketch" makes me suspicious of the use of the graph... The algebra does not lie!
Moreover, the solutions given in the problem are mirror images of each other: ( 2 1 , 4 1 ) and ( 4 1 , 2 1 ) .
But if the graphs pass through the line of symmetry (and there is no reason why they shouldn't), there must also be a solution that lies on that line, so that f ( x ) = f − 1 ( x ) = x . Therefore there are at least three solutions.
I was too lazy to prove that there were only three solutions. Calvin gives the argument nicely in terms of convexity.
The graphs in the problem are misleading. While they correctly show that both functions are decreasing and concave up, and symmetric about the y = x line, the conclusion of having only one intersection is unfounded. Nothing prevents two decreasing, concave up graphs from intersecting in more than one point: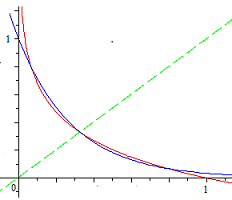
In fact, we will prove that there are three points of intersection: x = 4 1 , x = 2 1 and such x that lo g 1 / 1 6 x = x . To do this, consider the difference function: f ( x ) = lo g 1 / 1 6 x − ( 1 / 1 6 ) x . Its derivative, f ′ ( x ) = − x ln 1 6 1 + ( 1 / 1 6 ) x ln 1 6 . So f ′ ( x ) = 0 if and only if ( 1 6 1 ) x = x ( ln 1 6 ) 2 1 Taking logarithms of both sides, we get − x ln 1 6 = − ln x − 2 ln ( ln 1 6 ) This can be rewritten as ln x = ( ln 1 6 ) x + ln ( ln 1 6 ) . The left hand side is concave down, while the right hand side is linear, so they have no more than two points of intersection. Therefore, f ( x ) can have no more than three zeroes. We already know two of them: x = 4 1 and x = 2 1 , and from the Intermediate Value Theorem applied to the function lo g 1 / 1 6 x − x , there exists c such that lo g 1 / 1 6 c = c . For this c we have ( 1 / 1 6 ) c = c , so f ( c ) = 0 .
So, the original equation has exactly 3 solutions.