Logarithms
Evaluate the following:
9 lo g 3 ( 4 )
Do not use a calculator -- not even a slide rule!
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
41 solutions
we can do it this way too; let lo g 3 4 be x then by definition of logarithms 3 x = 4 ,we need 9 x , hence 16
Log in to reply
very amazingly nice!
Log in to reply
What do you studying? Because i am also 16 years.
Log in to reply
@Poovallal Vallal – all branches in mathematics by myself way in learning applying my theories
But, how did 3^{x} = 4?
Log in to reply
By definition of logarithms, if log a(b) = c, a^c = b. There you have it. Introducing a variable x, such that log 3(4) = x, by the definition above, 3^x = 4
Really Awesome!!!!!
I did the exact same thing and got it!
good solution
ok but when i used this method , we cant find 3^x=4 with out calculture i am used that solution
De donde sale el 4?
Wonderful solution!!,good observation
brilliant....
But if you square the 4 to get 16 wouldn't you square 3^x to get 9^x2???
NICE SOLUTION
by chance 9 + 3 + 4 equals 16 and 16 happens to be the answer.
Log in to reply
Without using LaTex the expression would be something like 9^(log3(4)), where "log3" means log base 3. If you plugged this expression into WolframAlpha you would get the answer 1 6 .
Log in to reply
What is La Tex and WolframAlpha?
Log in to reply
@Min Yue Yong – LaTex is the typesetting system used here on Brilliant,(and elsewhere); enter "LaTex" into the Search box to find out more about how to use it. WolframAlpha is a popular computational knowledge engine. I'll give you the link .
Log in to reply
@Brian Charlesworth – You just need a piece of paper and a pencil, or perhaps only your mind...
@Brian Charlesworth – I had no idea Tex still existed, I used it in my first full time job in 1985 and assumed it had been long superseded by word processors and other WYSIWYG software. It used to take hours for the computer to create readable text from the markup, I assume that has changed!
Log in to reply
@Bryoni Pidsley – I also recall how long the markup process took back then, but it's virtually instantaneous now. It's still the standard for the production of scientific writings.
I don't understand how you do the last one. Why 3^log3 (16) = 16?
Log in to reply
That step is explained in my note. If we let x = 3 lo g 3 ( 1 6 ) , then
lo g 3 ( x ) = lo g 3 ( 3 lo g 3 ( 1 6 ) ) = lo g 3 ( 1 6 ) .
(Note that in general lo g a ( a y ) = y for any a > 0 .)
So we end up with lo g 3 ( x ) = lo g 3 ( 1 6 ) , which, since the log function is one-to-one, implies that x = 3 lo g 3 ( 1 6 ) = 1 6 .
(Note that when I say that a function f ( x ) is one-to-one I mean that f ( x ) = f ( y ) if and only if x = y .)
By definition of logarithm to the base a, we have log x = log b hence x = b as the log fn is one to one
I did it with the same method!
That's the way I thought it too!
9 lo g 3 4 = x lo g 3 9 lo g 3 4 = lo g 3 x ( lo g 3 4 ) l o g 3 9 = lo g 3 x ( lo g 3 4 ) ( 2 ) = lo g 3 x 3 lo g 3 4 2 = 3 lo g 3 x 1 6 = x
simple and feasible explanation.....nice!!
good explanation
Great solution, easy to follow.
whoao u rock buddy ! (y) got it
I used the same method.
i like it this way ... nice one sir ...
Good solution! But why have you added the number 3 on the last step?? Is it wrong to write just log(3) 4^2 = log(3) x ?
Log in to reply
I guess there is nothing wrong with your approach. I only add the number three in the last step cause I thought it would be more easy to see the answer.
Simple one
By rules of logarithms,
x l o g a b can be written as b l o g a x That makes things much more simpler.
THATS IT buddy, you're the man
Much simpler explanation!
yeah.. you got it bro
Let
x
=
l
o
g
3
(
4
)
.
Then we know that
3
x
=
4
.
We want
9
x
.
So we can do this:
9
l
o
g
3
(
4
)
=
9
x
=
(
3
2
)
x
(
3
2
)
x
=
3
2
x
=
3
x
×
3
x
And since
3
x
=
4
, we're left with
4
×
4
=
1
6
.
Moderator note:
Great! That is the correct usage of the rules of exponents.
best, the simplest
Simple solution, yet amazing!
Firstly, take a moment to understand this proof:
If x = y lo g b a
Then, by taking log on both sides, we get lo g b x = lo g b ( y lo g b a )
Using the identity lo g n ( m x ) = x lo g n m
lo g b x = ( lo g b a ) lo g b y
lo g b x = ( lo g b y ) lo g b a
lo g b x = lo g b ( a lo g b y )
Removing log, x = a lo g b y
So therefore, combining the first and last statements, we get y lo g b a = a lo g b y
Moving on to the problem at hand:
Given x = 9 lo g 3 ( 4 )
Using the above identity, we get
x = 4 lo g 3 ( 9 )
x = 4 2
x = 1 6
Excelente, voy a tomar nota de esto en mis apuntes destacados. I LIKE so much
I will take note of this in my affairs highlight
I'd like to meet and try some mathematical issues with you. e-mail: [email protected]
How did you put that paper in the box? Brilliant e-mail [email protected]
9 lo g 3 4 = ( 3 lo g 3 4 ) 2 = 4 2 = 1 6
L e t x = lo g 3 4 S o 9 l o g 3 ( 4 ) = 9 x B u t ; l o g 3 4 ⇔ 3 x = 4 ⇒ 3 x = 4 ( S q u a r e b o t h s i d e s ) ⇒ 3 2 x = 4 2 ⇒ ( 3 2 ) x = 1 6 ⇒ 9 x = 1 6 ∴ 9 l o g 3 ( 4 ) = 1 6
Let x = 9 lo g 3 4 , we take logs on both sides to get log(x)=2log4, this implies that x = 1 6 .
there is a rule...I don't have explanation now 9^log3(4) = 4^log3(9) you can actually rotate or swap the numbers, value remains the same.
Since a^logb c ( actually b is the base and a is input) = c^logb a( same as above) Therefore, the above statement can be rewritten as 4^log3 3^2=4^2=16
First, we can say 9 = 3^2.
Then, 9 lo g 3 ( 4 ) = 3 2 lo g 3 ( 4 )
Using the power property, 2 lo g 3 ( 4 ) = lo g 3 ( 1 6 )
Now, using the Logarithmic Rules of Exponents, a lo g a ( b ) = b
Substituting all the values, we get 3 lo g 3 ( 1 6 ) = 1 6
Finally, we can conclude the solution to be 1 6 .
Moderator note:
Simple standard approach.
Does using Fermi's solution count? (i.e. I looked and guessed)
9 l o g 3 ( 4 ) = t,
taking log to the base e both sides,we have,
[ l o g 3 ( 4 ) ] ∗ l o g 9 = log (t).
[ l o g 3 ( 4 ) ] ∗ 2 l o g ( 3 ) =log (t)
l o g e ( 3 ) l o g e ( 4 ) *2log(3)) = log (t)
2 ∗ l o g ( 4 ) =log (t)
l o g ( 4 ) 2 =log (t)
log 16 =log (t)
hence.t=16,ans.
This is simpler imho:
9 lo g 3 ( 4 ) = = = = ( 3 × 3 ) lo g 3 ( 4 ) ( 3 lo g 3 ( 4 ) ) × ( 3 lo g 3 ( 4 ) ) 4 × 4 1 6
Let be l o g 3 ( 4 ) = x , so 3 x = 4 and since 9 = 3 2 it means that the result is the square of 4 so 16
P=9^log3 (4) take log for two sides for base 4 log4 (p)=log3 (4)×log4 (9)=log3 (9)=2 so p=4^2=16######
let A=9^log(3)4 let B=log(3)4
Then A=3^2B and 3^B=4 (by logarithm)
then A=16
Do not try to memorize formulas or theorems ; just do it yourself
9 l o g 3 ( 4 ) = ( 3 2 ) l o g 3 ( 4 ) = ( 3 l o g 3 ( 4 ) ) 2 = 4 2 = 1 6
you can rewrite that as log(base)9(of)x = log(base)3(of)4. Then, log(base)3^2(of)x can also be written as log(base)3(of)x^(1/2). Once the two expression on either side of the equal sine share the same base, you can set 4 equal to the square root of x, and therefore x is 16.
let>> x=9^log3(4)
log3(x)=log3(9^log3(4))= log3(4)* log3(9)=log3(4)*2= 2 log3(4) = log3(4^2)
so x=4^2= 16
9^{log3(4)}=4^log3(9)
= 4^ log3(3^2)
= 4^ 2log3(3)
= 4^ 2(1)
= 4^2 = 16
By luck babieesssssss ssssss
m^log b(n)=n^log b(m) hence question=4^log_3(9)=4^2
Lets suppose .... x= 9^log3 (4)....... x= 3^2*log3 (4).... x = 3^log3(4^2).....x=3^log3(16)......taking both sides log3.... log3(x)=log3[3^log3(16)]....... log3(x)=log3(16)log3(3).... log3(3)=1.....so log3(x)=log3(16).... by cancelling log3 on both sides we get.... x=16....hence.... 9^log3 (4)=16
Let 9^{log3 (4)} = x
Now, 3^2{log3 (4)} =x
Or,3{log3 (4^2)} =x
Now according to formula, we obtain, x= 4^2=16.
Log a(b) = log a^c(b^c) (proof at the bottom) Log 3(4) = log 9(16) 9^log_9(16) = 16
PROOF Log a^c(b^c) = log(b^c) / log(a^c) = c*log(b) /c*log(a) =log(b) / log(a) =log a(b)
X=9^(log₃4) log₃X=log₃4 log₃9=2 log₃4=log₃16 X=16
9^log3(4)
=> 3^2.log3(4)
m. log a= log a^m
therefore
3 ^log3(4^2)
if f(x)^log f(x) (X) = X ........... here f(x) is base in log
therefore
3^log3(4^2)= (4^2)=16 ....Ans
9^{log 3(4)}=3^2{log 3(4)}=3{log 3(4^2)}= 3{log 3(16)}= 16
9^log3(4)=3^log3(16) now go to basic knowledge, log3(16) means the exponent of 3 that will make it 16. suppose this exponent is x. so now we get 3^log3(16)=3^x=16. Bingo.
Say , y=9^[ log 4 to base 3 ].
Applying logarithms to base 3 on both sides ,
log y to base 3 = [ log 9 to base 3 ] * [ log 4 to base 3]. = 2 [ log 4 to base 3]. = [ log 4^2 to base 3 ]. = [ log 16 to base 3 ].
Comparing the arguments on both sides, y = 16.
Hence , 9^ [ log 4 to base 3 ] = 16.
9^log3(4) = 4^log3(9) = 4^2 = 16
you could also turn 3^(2log(3)(4)) into (3^log(3)(4)) (3^log(3)(4)) which intern equals 4 4=16
Let log_{3}(4)=y
4 = 3^{y}
squaring both sides
16 = 9^{y}
Hence 9^{log_{3}(4)} = 16
9^(log3(4)) = (3^2)^(log3(4)) = 3^(log3(4^2)) = 3^(log3(16)) = 16
9^(log3(4))=3^(2(log3(4)))=3^(log3(16))=16
9^(log3(4))=3^(2(log3(4)))=3^(log3(16))=16
Let X=given function.
than take log both side,
apply the basic principles of logarithms,
we get 16.
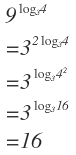
9 lo g 3 ( 4 ) = 3 2 ∗ lo g 3 ( 4 ) = 3 lo g 3 ( 4 2 ) = 3 lo g 3 ( 1 6 ) = 1 6 .
Note that, in general, if x = a lo g a ( b ) then lo g a ( x ) = lo g a ( a lo g a ( b ) ) = lo g a ( b ) .
Now since the log function is one-to-one, we can conclude that x = b .