Logicians escape
 8 logicians,
Calvin
,
Azhaghu
,
Ishan
,
Nihar
,
Brian
,
Sandeep
,
Tanishq
and
Prasun
are being chased by the deadly medieval monster, Amphisbaena.
8 logicians,
Calvin
,
Azhaghu
,
Ishan
,
Nihar
,
Brian
,
Sandeep
,
Tanishq
and
Prasun
are being chased by the deadly medieval monster, Amphisbaena.
Before them is a bridge, their only hope for survival. The bridge can only hold at most 2 persons at a time. Since it is pitch dark they have to carry a lamp, which has to be walked back and forth the two ends.Each person walks at a different speed. A pair must walk together at the speed of the slower person.
They have to cross the bridge in the minimum possible time, or else they will be engulfed in the pangs of death. What is the minimum time that the logicians would have planned out (in minutes)?
Details and Assumptions :
-Crossing time: Calvin-2 minutes, Azhaghu- 3 minutes, Ishan-5 minutes, Nihar-7 minutes, Brian-11 minutes, Sandeep- 13 minutes, Tanishq- 17 minutes, Prasun- 19 minutes.
- Strategies such as throwing the lamp across the bridge etc are not allowed.
Inspired from this game .
This question is part of the set Best of Me .
The answer is 66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Yes, that's the optimal approach. A general solution for the bridge-crossing puzzle is provided in this paper .
Log in to reply
Thanks for sharing that link.
I decided to look at the comments here, in large part to see whether anyone had posted a proof that 66 is the minimum; but I didn't anticipate anything as extensive as the paper.
:)
66 is correct! For simplicity I will use time in mins required to travel by respective person s instead of theirs names. 1st trip by 2,3 & 2 goes back = 5 mins 2nd trip by 19,17 & 3 goes back= 22 mins 3rd trip by 2,3 & 2 goes back = 5 mins 4th trip by 13,11 & 3 goes back =16 mins 5th trip by 2,3 & 2 goes back= 5 mins 6th trip by 7,5 & 3 goes back= 10 mins Last trip by 2,3 = 3 mins Hence total (5+22+5+16+5+10+3) 66.
Br, Ganesh Dhure
If Calvin has returned the lamp, how ll he be coming back to the other side of the bridge?? My answer s 87
My answer is 87 .it is the minimum time needed because the bridge can hold atmost 2 people at a time.
Log in to reply
Yes, so you first send Calvin (2) and Azaghu (3). Calvin brings back the lamp and Ishan (5) and Nihar (7) cross. Now Azaghu (3) returns the lamp. Calvin (2) and Azaghu (3) cross again and Calvin (2) returns the lamp. Now (11) and (13) cross and (3) returns the lamp. Calvin (2) and Azaghu (3) cross again and Calvin (2) returns the lamp. (17) and (19) cross and Azaghu returns the lamp. Finally Azaghu and Calvin cross the bridge. Adds up to 66 like Brian Charlesworth said.
Log in to reply
I get 87 as well. First AZ and Calvin Cross which takes 3, then AZ must bring the lamp back across with him which takes 2 minutes then AZ brings the next person ISHAN which takes 5 minutes then Calvin must bring the lamp back across the bridge which takes 2 minutes and so on.
I agree with 87. I don't see how this is 66.
Log in to reply
The times of the trips taken as outlined sum to
3 + 2 + 7 + 3 + 3 + 2 + 1 3 + 3 + 3 + 2 + 1 9 + 3 + 3 = 6 6 .
TED also has a video on a shorter version of 4 people here - Can you solve the bridge riddle? .
The answer is 66. Two people can cross at once so the total does not need to be as large as the sum of everybody's individual crossing times. A full movement is detailed below:
1: Calvin & Azaghu cross (3 mins - total 3 mins)
2: Calvin returns (2 mins - total 5 mins)
3: Tanish & Prashun cross (19 mins - total 24 mins)
4: Azaghu returns (3 mins - total 27 mins)
5: Calvin & Azaghu cross (3 mins - total 30 mins)
6: Calvin returns (2 mins - total 32 mins)
7: Brian & Sandeep cross (13 mins - total 45 mins)
8: Azaghu returns (3 mins - total 48 mins)
9: Calvin & Azaghu cross (3 mins - total 51 mins)
10: Calvin returns (2 mins - total 53 mins)
11: Ishan & Nihar cross (7 mins - total 60 mins)
12: Azaghu returns (3 mins - total 63 mins)
13: Calvin & Azaghu cross (3 mins - total 66 mins)
And everyone is now across the bridge.
Ishan and Calvin 5 Calvin return 2 Calvin and azaghu 3 Calvin return 2 Brian and Sandeep 13 Azaghu return 3 Calvin and nihar 7 Calvin return 2 Calvin and azaghu 3 Calvin return 2 Tanishq and parsun 19 Azaghu return 3 Calvin and azaghu 3 67 min in total bUt Calvin will make 4returns
First of all there is no way this solution can be 66.
Since Calvin is the fastest you have to use him to return the lamp every single time.
Then you add up the time of each person plus Calvin's return trips.
This gives a total of 87.
I know you may not have an infinite number of staff members, But at least you should verify that the solutions to the problems are the correct one. That way you can avoid atrocities like this one. And we problem solvers do not waste our time. !!
At first I had this same opinion but the answer explains how you can save time. With the solution of 87, only 1 person is crossing every time there is a round trip "trip," except for the very last one. Here, there are opportunities for two to cross at once effectively.
The thing is- You shouldn't send the fastest one every single time. If there is already one of the 2 fastest people on the other side, you can send the slower ones together where you will only have to count the time of slowest person!
It definitely can be 66. Two people can cross at once so the total does not need to be as large as the sum of everybody's individual crossing times. Observe: 1: Calvin & Azaghu cross (3 mins - total 3 mins) 2: Calvin returns (2 mins - total 5 mins) 3: Tanish & Prashun cross (19 mins - total 24 mins) 4: Azaghu returns (3 mins - total 27 mins) 5: Calvin & Azaghu cross (3 mins - total 30 mins) 6: Calvin returns (2 mins - total 32 mins) 7: Brian & Sandeep cross (13 mins - total 45 mins) 8: Azaghu returns (3 mins - total 48 mins) 9: Calvin & Azaghu cross (3 mins - total 51 mins) 10: Calvin returns (2 mins - total 53 mins) 11: Ishan & Nihar cross (7 mins - total 60 mins 12: Azaghu returns (3 mins - total 63 mins) 13: Calvin & Azaghu cross (3 mins - total 66 mins) And everyone has crossed.
Come on bro don't just say things without checking or understanding the solution....and that thing works , here's how: total time can be broken into two categories 1. total returning time 2. Total going time by your assumption you are just minimising the 1st part, not the second one.. But if you follow the given solutions an optimum time minimising the both quantities is obtained..
Nos. indicate time taken 2,3 -> go 2 <- returns 19,17 -> go 3 <- returns 2,3 -> go 2 <- returns 13,11 -> go 3 <- returns 2,3 -> go 2 <- returns 5,7 -> go 3 <- returns 2,3 -> go That's it. All have crossed.
The problem does not, does not, does not, say that someone could begin to move while they come to get him !!
Python code to solve this problem
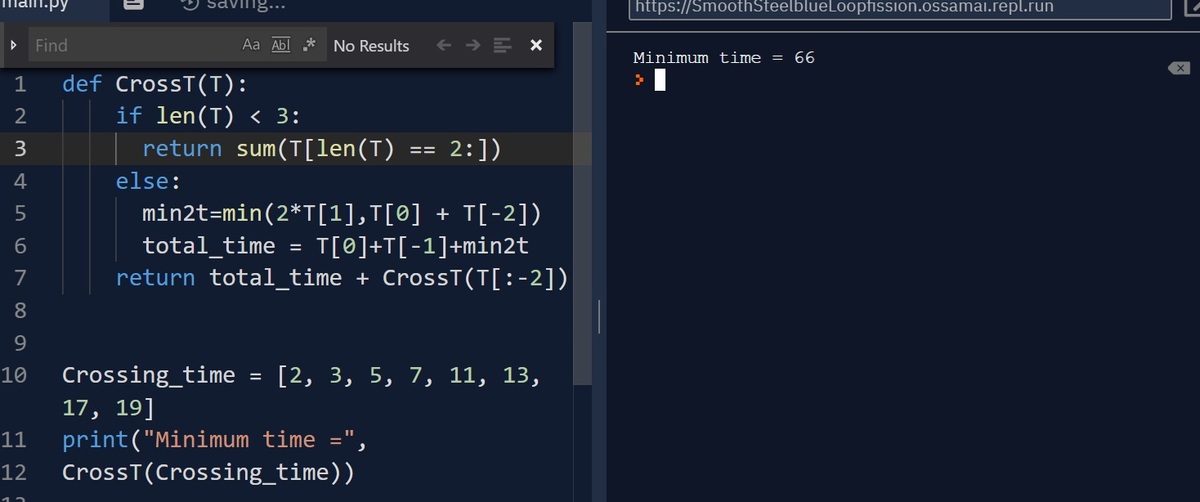
There are several things to consider for answering this problem: 1. 2 people with the similar crossing time should cross together. 2. Fastest people should cross back to return the lamp.
Start with Calvin (2) and Azhaghu (3) to cross the bridge, and Calvin return the lamp. Then Ishan (5) and Nihar (7) cross the bridge, and Azhaghu return the lamp. Start again with Calvin and Azhaghu to deliver Brian (11) and Sandeep (13), and so on.
The total process takes 66 mins. (Hopefully they make it on time ...)