Looks Like Gabriel's Horn To Me

Calculus Level 5

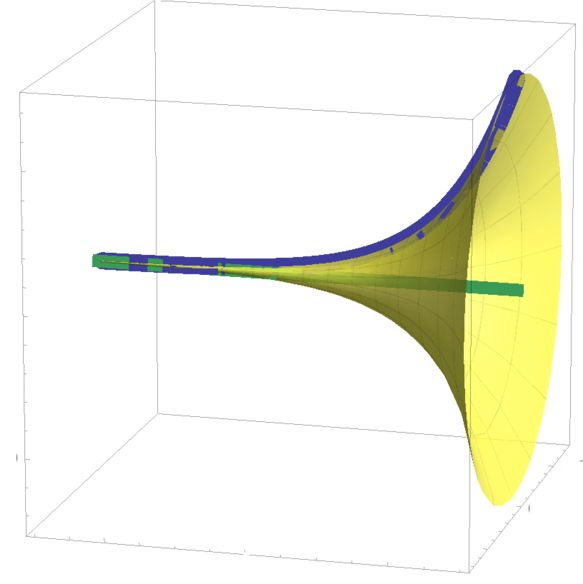
An infinitely long cone can be generated by revolving the following curve about the $x$ -axis.

$y = e^{x}, \quad x < 0$

If the ratio of volume to lateral surface area of the cone is $\beta$ , then what is $\lfloor 10^4 \times \beta \rfloor$ ?

Notation : $\lfloor \cdot \rfloor$ denotes the floor function .

The answer is 2178.

1 solution

Aditya Kumar
Feb 28, 2016

Volume of a function $f(x)$ when revolved about $x$ -axis is given by: $\displaystyle V=\pi \int _{ a }^{ b }{ { \left( f\left( x \right) \right) }^{ 2 } \, dx }$

Here, $f\left( x \right) ={ e }^{ x }$ , $a=-\infty$ and $b=0$ ,

Therefore, on integrating we get $V=\dfrac{\pi}{2}$

Lateral surface area of a function $f(x)$ when revolved about $x$ -axis is given by: $\displaystyle L=2\pi \int _{ a }^{ b }{ { \left( f\left( x \right) \sqrt { 1+{ \left( f'\left( x \right) \right) }^{ 2 } } \right) }dx }$

Now we, get : $L=2\pi \int _{ -\infty }^{ 0 }{ \left( { e }^{ x }\sqrt { 1+{ e }^{ 2x } } \right) dx } \\ L=2\pi { \left[ \frac { 1 }{ 2 } \left( { e }^{ x }\sqrt { 1+{ e }^{ 2x } } +\sinh ^{ -1 }{ { e }^{ x } } \right) \right] }_{ -\infty }^{ 0 }\quad$

Therefore, $L\approx7.2118$ .

Hence, we get $\boxed{\left\lfloor 10000\times \frac { V }{ L } \right\rfloor =2178}$ .

I think an interesting result is to allow $x\rightarrow \infty$ . Then the ratio becomes exactly $\dfrac{1}{2}$ .

Michael Mendrin - 5 years, 3 months ago

That is interesting. Even if we integrate from $\dfrac{x}{2}$ to $x$ and let $x \to \infty$ we still get a ratio of $\dfrac{1}{2}$ . I'm not sure what happens, though, if we integrate from $\alpha x$ to $x$ and let $\alpha \to 1^{-}$ and $x \to \infty$ .

Brian Charlesworth - 5 years, 3 months ago

Yes, if we integrate from $a$ to $b$ , where $b>a>0$ , it turns out that as $b>a\rightarrow\infty$ , then in the limit, the ratio is always $\frac{1}{2}$ . In other words, the final result is dependent on "what's over there infinitely far away", independent of the dimensions of the horn at finite distances from the origin. The limit can be worked out roughly as follows. Given $b>a>0$ , the surface area and volume, expressed in exponential form, are

$V={ \pi e }^{ a+b }\left( { e }^{ a-b }-{ e }^{ -a+b } \right)$

$S=2\pi \left( { e }^{ a }\sqrt { 1+{ e }^{ 2a } } -{ e }^{ b }\sqrt { 1+{ e }^{ 2b } } +Log\left( { e }^{ a }+\sqrt { 1+{ e }^{ 2a } } \right) -Log\left( { e }^{ b }+\sqrt { 1+{ e }^{ 2b } } \right) \right)$

but for large $a, b$ , the second expression can be simplified to

$S=2\pi \left( { e }^{ 2a }-{ e }^{ 2b }+a-b \right)$

so that the fraction $\dfrac{V}{S}$ becomes

$\dfrac { V }{ S } =\dfrac { 1 }{ 2 } \dfrac { { e }^{ a-b }-{ e }^{ -a+b } }{ { e }^{ a-b }-{ e }^{ -a+b } } =\dfrac { 1 }{ 2 }$

as $b>a\rightarrow\infty$

Michael Mendrin - 5 years, 3 months ago

@Michael Mendrin – Great! Thanks for the analysis. Doing the same with polynomial functions has the $\frac{V}{S}$ ratio always going to infinity, so we need exponential growth for $S$ to at least "keep pace" with $V$ . Is there any significant interpretation of this result in the realm of physics? It feels like this is more than just a curiosity.

Brian Charlesworth - 5 years, 3 months ago

@Brian Charlesworth – Well, Brian, the oddity about this problem is that we're dividing an area by a volume. That's not very physical. But let me come back later with a sort-of intuitive explanation for this result.

Michael Mendrin - 5 years, 3 months ago

Looks Like Gabriel's Horn To Me

The answer is 2178.

1 solution

0 pending reports