Divisible by 6

Recall the algebraic identity

${ 1 }^{ 2 }+{ 2 }^{ 2 }+{ 3 }^{ 2 }+\cdots +{ n }^{ 2 }=\sum _{ i=1 }^{ n }{ n^{ 2 } } =\frac { n\left( n+1 \right) \left( 2n+1 \right) }{ 6 }$

Now, multiplying both sides by 6 gives us

$6\sum _{ i=1 }^{ n }{ n^{ 2 } } =n\left( n+1 \right) \left( 2n+1 \right).$

Because LHS is a multiplication of an integer and another integer that is the sum of squares of integers, then RHS is a natural number multiplied by 6.

Hence, $n\left( n+1 \right) \left( 2n+1 \right)$ is divisible by 6 for all natural numbers $n$ .

My approach was as follows. Since one of $n$ or $n + 1$ must be even we know that the given product is divisible by $2$ . Now if either $n$ or $n + 1$ is divisible by $3$ then the given product is divisible by $2*3 = 6$ . If neither $n$ nor $n + 1$ is divisible by $3$ then $n + 2$ must be divisible by $3$ , since precisely one of three consecutive integers is divisible by $3$ . But then with $n + 2 = 3m$ for some integer $m$ we find that

$2n + 1 = (3n + 3) - (n + 2) = 3(n + 1) - 3m = 3(n + 1 - m)$ ,

which means that $3|(2n + 1)$ , and hence $6|n(n + 1)(2n + 1)$ .

$2n + 1 = (n - 1) + (n + 2)$

$\therefore n(n + 1)(2n + 1) = (n - 1)(n)(n + 1) + (n)(n + 1)(n + 2)$

$3! = 6 | k(k + 1)(k + 2)$ where $k \in N$

$\therefore 6| (n - 1)(n)(n + 1) + (n)(n + 1)(n + 2)$

$\Rightarrow 6|n(n + 1)(2n + 1)$

This can be proved by using induction on n

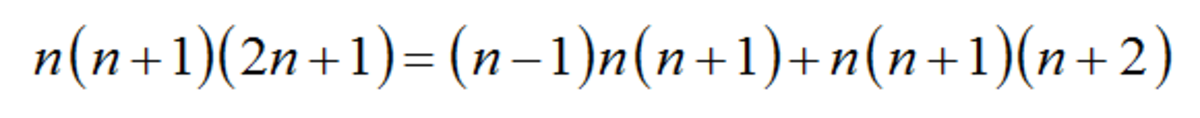
One of two consecutive integers is divisible by 2.

One of three consecutive integers is divisible by 3.

Therefore the multiple of three consecutive integers is divisible by 6.

My solution: Call $A=n(n+1)(2n+1)$ Mutiply $A$ by 4, we get: $4A=(2n)(2n+1)2(n+1)=2n(2n+1)(2n+2)$ In two even numbers, $2n$ and $2n+2$ , there exist a number which is divisible by $4$ , and the others is divisible by $2$ .Beside that, these are 3 consecutive integer, so there is also exist a number which is divisible by $3$ , so $(4 \times 3 \times 2)|4A$ $\iff 24|4A$ $\Rightarrow \frac{24}{4}|\frac{4A}{4}$ $\iff \boxed{6|A}$

2n+1=n+(n+1). The number n(n+1)(2n+1) is a product of two consecutive numbers multiplied by their sum. One of the two consecutive number has to be even, so the product is divisible by 2. If n and n+1 are not divisible by 3, then their sum has to be divisible by 3 because n and n+1 when divided by 3 would leave a remainder of 1 & 2 respectively and therefore, their sum would leave a remainder of 1+2=3 i. e. would be divisible by 3. Hence the number is divisible by 6.

Let f(n) = n(n+1)(2n+1), where n is an element of the set of positive integers. f(1) = 1×2×3=6, which is divisible by 6. Assume that for n=k, f(k) = k(k+1)(2k+1) is divisible by 6 for all positive integer values of n. Therefore f(k+1) = (k+1)(k+1+1)(2(k+1)+1) = 2k^3 + 9k^2 + 13k + 6 f(k) can also be written as f(k) = 2k^3 + 3k^2 + k Therefore f(k+1)-f(k) = 2k^3 + 9k^2 + 13k + 6 - 2k^3 -3k^2 - k = 6k^2 + 12k + 6 = 6(k^2 + 2k + 1) So f(k+1) = f(k) + 6(k^2 + 2k + 1) Therefore f(n) is divisible by 6 when n=k+1 If f(n) is divisible by 6 when n=k, then it has been shown that f(n) is also divisible by 6 when n=k+1. As f(n) is divisible by 6 when n=1, f(n) is also divisible by 6 for all positive integers by mathematical induction.