Lovely Dynamics of Friction in Semicircle
A rough semicircle of equation
x
2
+
y
2
=
1
,
y
≤
0
is fixed at coordinate
R
(
0
,
−
1
)
.
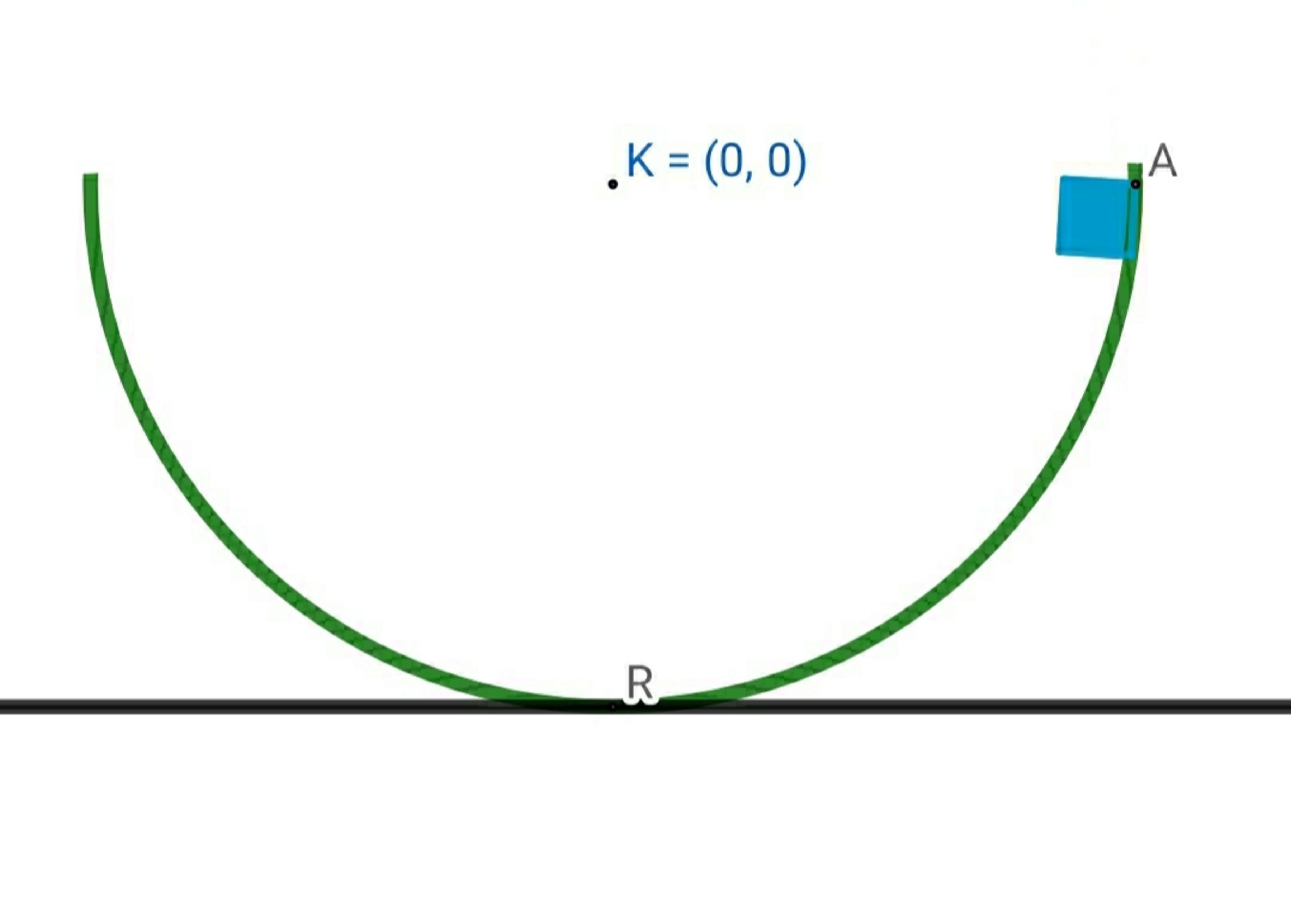
The Blue block is released from rest ,from
A
(
1
,
0
)
Find the time for which the block stops for the first time.
Details and Assumptions
- Friction coefficient of semicircle μ = 0 . 5 .
- Mass of blue block M = 1 .
- g = 1 0 ,assume uniform in every moment.
- Consider everything in SI units.
This problem is dedicated to my respected teacher Karan Chatrath
The problem is original.
The answer is 1.02.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I have used the diagram that you shared but I have not resolved the forces along the tangential and normal directions. FYI
@Karan Chatrath Thanks and very impressive solution.
Log in to reply
Welcome. Nice problem
Log in to reply
@Karan Chatrath sir is it necessary that the block comes for forever rest at
(
0
,
−
1
)
Can't the block comes at forever rest at some
θ
angle ?
Please share your views
Thanks in advance
Hey bro, why'd you delete the new algebra problem?
Log in to reply
@Krishna Karthik
I got the solution. And it was not a hard problem.
And also a not original problem.
.I always try my best to post, tricky, hard, coneptual, original problems.
BTW bro when you are going to make notes on Simpson 1/3 rd 3/8, rules.
I am eagerly waiting.
Thanks in advance.
Log in to reply
@A Former Brilliant Member – Alright, let's do that today. See you!
To answer your question: Whether the block comes to rest at ( 0 , − 1 ) depends on the friction coefficient. For example, if the friction coefficient is 0.5, then the block comes to rest at θ = 0
If you reduce the friction value to say 0.02, the block exhibits damped oscillations until it eventually settles very close to θ = 0 .
Log in to reply
@Karan Chatrath
sir I think for this problem it finally comes to rest at -10 degrees.
BTW thanks for this interesting result.
Hey mate, I just solved your problem. Nice one! Loved it😁👍🏽 There are already two pretty comprehensive solutions out there. I used the computational approach that Steven Chase used. I want to know what method you used @Neeraj Anand Badgujar . Tell me in the comment section.
Firstly, there are 3 forces acting on the object;
The Tangential Gravitational Force
Where θ is the angle of the slope/tangent line to the circle, the force acting tangentially to the circle (due to gravity) is:
F g t = m g sin ( θ )
The value of θ can be given by finding tan − 1 ( ) of the slope, given by tan − 1 ( 1 − x 2 x )
The Normal Force
The normal force acting down a ramp dependent on the cosine of the ramp angle. N = m g cos ( θ ) + R m v 2
The Frictional Force
The frictional force is F f r i c t i o n = μ N , and is positive or negative depending on the velocity of the object.
Once you carry out these computations and numerically integrate the acceleration, you can get the result. Here's my code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
|
@Krishna Karthik
I solve analytically and some help with Karan sir.
Thanks for your solution. (Upvoted)
Log in to reply
Brilliant solution from Chatrath sir, I think. Great!
Nice problem. Simulation code is below, with comments. The block takes 1 . 0 2 seconds to come to a stop, and it travels through an angle of 9 8 . 7 degrees
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
|
@Steven Chase
sir I am not able to understand the solution (5th and 6th step) of this problem?
Can you help me in explaining?

Thanks in advance
Hope you will reply .
Log in to reply
You gotta start posting in the notes section to get more people to notice this.
The 5th/6th step involved quotient rule .
Log in to reply
@Pi Han Goh
sir I don't think it is quotient rule.
I think
x
is replaced by
2
x
Log in to reply
@A Former Brilliant Member – Oh, that.
x → 0 lim f ( x ) = 2 x → 0 lim f ( 2 x ) . You're just replacing x with 2 x . That's nothing fallacious about this, as long as you know that 2 x is also continuous at x = 0 .
Log in to reply
@Pi Han Goh – @Pi Han Goh sir explain the step 5 to 6??
Log in to reply
@A Former Brilliant Member – Instead of repeating what you said, try to elaborate on why you fail to understand a certain step. I already said it's quotient rule, but you said you were referring to some other step. Please try to be more explicit about what you're asking.
Log in to reply
@Pi Han Goh – @Pi Han Goh I just want to know that after 5th step how does the 6th step come???
Log in to reply
@A Former Brilliant Member – I already told you it's quotient rule. If you think I misunderstood what you said, please elaborate more on this.
What you're basically communicating to me is
"Hey, tell me why this happens?"
"Okay, it's because of X"
"No, I mean that."
"Okay, it's because of Y"
"No, I mean the first one"
"Well, I just told you it's X"
"No, I mean the first one"
"What more do you want me to say? It's X for crying out loud!"
Either be more explicit, or I won't bother helping you again.
Log in to reply
@Pi Han Goh
–
@Pi Han Goh
ok I got it.
How to make GIF in python ??
Log in to reply
@A Former Brilliant Member – I don't know.
Log in to reply
@Pi Han Goh – @Pi Han Goh what should I learn in python which will help me in future??
Log in to reply
@A Former Brilliant Member – That depends on what you want to do.
For most, Python is just to do complex calculations.
First start by learning how to differentiate polynomials and matrices on Python. And learn how to automate all the school homework by Python... (At least, that's how I would want to do it)
@A Former Brilliant Member – Bro how do you come up with all these questions so rapidly? lmao...
@Pi Han Goh – Lol such a funny conversation... I'm dying🤣XD
Log in to reply
@Krishna Karthik – @Krishna Karthik Ya bro because after saying so many times @Pi Han Goh was not understanding, thats why I just said 'I got it's.
Log in to reply
@A Former Brilliant Member – Oh yeah. True. He kept going on about quotient rule when it was actually a trig identity. Fair enough.
Log in to reply
@Krishna Karthik
–
@Krishna Karthik
bro I think he is in love with quotient rule.
Just joking
See my new problem of algebra
And if possible post the solution
Thanks in advance
@A Former Brilliant Member – Hey bud, I'm also posting a solution to this problem here. I hope you'll look at it once it's out!
Log in to reply
@Krishna Karthik – @Krishna Karthik you are welcome bro.
I don't think it is the quotient rule. There is no differentiation taking place here. I think that the following identity is used:
tan ( 2 x ) = 1 − tan 2 x 2 tan x
Log in to reply
@Karan Chatrath – @Karan Chatrath E x a c t l y
@Karan Chatrath – @Pi Han Goh sir above @Karan Chatrath sir said that , we are not using quotient rule.
@Steven Chase
what to do after this
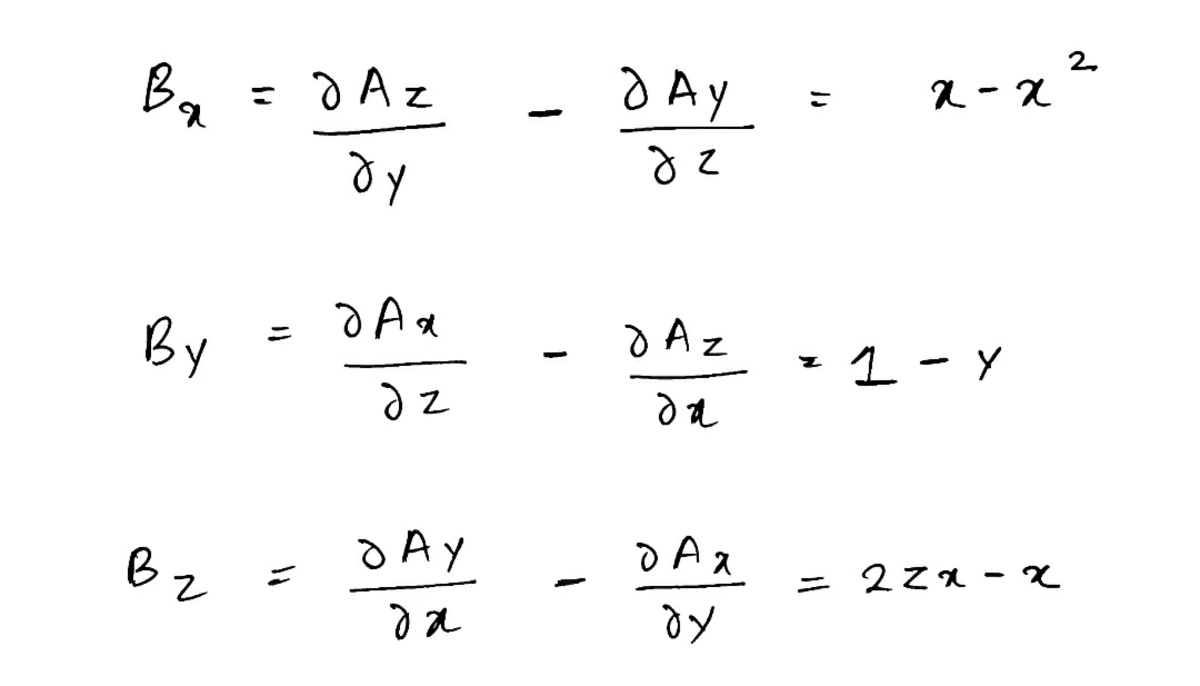 Thanks in advance
Thanks in advance
Log in to reply
Double-check your result for B z . And then you can do any one of the following three things:
1)
Integrate
B
over the given surface
2)
Integrate
B
over some other open surface that has the same boundary curve as the given surface
3)
Integrate
A
over the boundary curve
The second and third procedures are equivalent because of Stoke's theorem
Log in to reply
@Steven Chase I want to use
2)
method
Integrating over the boundary is
4
x
2
+
1
y
2
=
1
Am I right
Log in to reply
@A Former Brilliant Member – The boundary curve is not at z = 0
Log in to reply
@Steven Chase
–
@Steven Chase
sir now is it correct
9
3
2
x
2
+
9
8
y
2
=
1
??
@Steven Chase – @Steven Chase sir next???
Log in to reply
@A Former Brilliant Member – Evaluate the integral over that curve:
∫ A ⋅ d ℓ
Log in to reply
@Steven Chase
–
@Steven Chase
But sir what is
A
in the above integral and how to evalute it?
I know I am disturbing you a lot in this , but please
Log in to reply
@A Former Brilliant Member – It is the vector magnetic potential that is given in the problem
Log in to reply
@Steven Chase – @Steven Chase should I write d l in polar form or in what?
Log in to reply
@A Former Brilliant Member – However you like
Log in to reply
@Steven Chase
–
@Steven Chase
am I going right
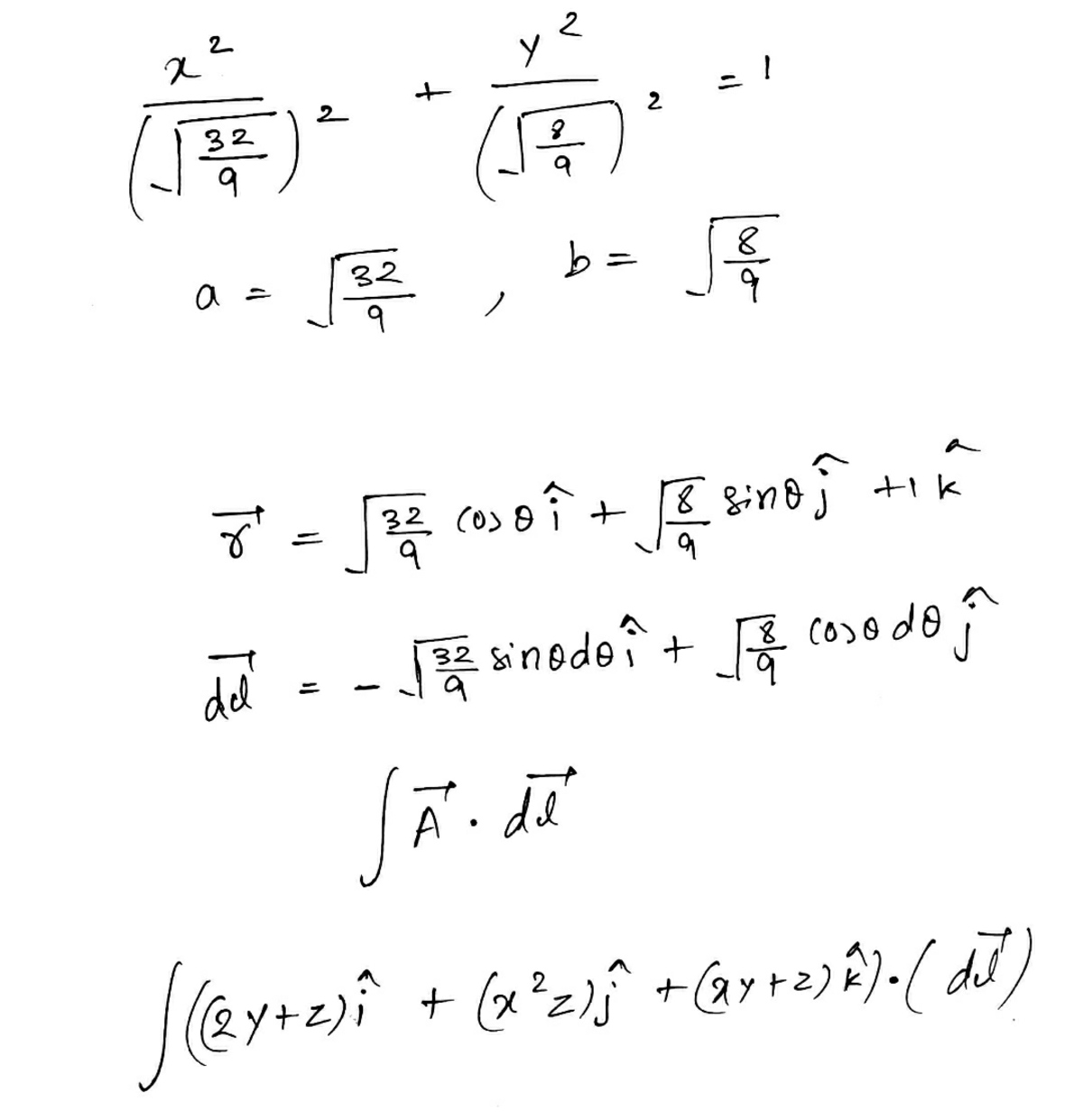
Please reply
I don't know much about this type of question therefore it is getting hard for me
Hope you will reply.
Log in to reply
@A Former Brilliant Member – What final result do you get? Also, you can make use of a computational approach if necessary.
Let the x and y coordinates of the particle be:
x = sin θ ⟹ x ˙ = cos θ θ ˙ ⟹ x ¨ = cos θ θ ¨ − θ ˙ 2 sin θ y = − cos θ ⟹ y ˙ = sin θ θ ˙ ⟹ y ¨ = sin θ θ ¨ + θ ˙ 2 cos θ
Applying Newton's second law along the X and Y directions gives:
m x ¨ = f cos θ − N sin θ m y ¨ = N cos θ + f sin θ − m g f = μ N
Solving for θ ¨ by eliminating N gives after simplification:
θ ¨ = μ θ ˙ 2 − g sin θ + μ g cos θ ⟹ θ ¨ = 2 θ ˙ 2 − 1 0 sin θ + 5 cos θ ⟹ θ ¨ − 2 θ ˙ 2 = 5 ( cos θ − 2 sin θ )
⟹ θ ˙ d θ d θ ˙ − 2 θ ˙ 2 = 5 ( cos θ − 2 sin θ )
Multiplying both sides by e − θ and simplifying:
⟹ d θ d ( e − θ 2 θ ˙ 2 ) = 5 e − θ ( cos θ − 2 sin θ )
When \t = 0 then θ = π / 2 and θ ˙ = 0 . Using these initial conditions, separating the variables and integrating gives:
⟹ e − θ 2 θ ˙ 2 = ∫ π / 2 θ 5 e − θ ( cos θ − 2 sin θ ) d θ ⟹ e − θ 2 θ ˙ 2 = 5 ( 2 e − θ ( 3 sin ( θ ) + cos ( θ ) ) − 2 3 e − 2 π ) θ ˙ = − 5 ( 3 sin ( θ ) + cos ( θ ) − 3 e − 2 π + θ )
The minus sign is introduced since as t increases, θ decreases. By plotting the RHS of the above equation, one can easily see that it becomes zero at θ = θ o ≈ − 0 . 1 5 1 4 2 8 r a d
Now, separating variables and integrating gives:
T = ∫ θ o π / 2 5 ( 3 sin ( θ ) + cos ( θ ) − 3 e − 2 π + θ ) d θ ≈ 1 . 0 2 s